闫氏dp分析法区间dp（笔记）（含有y总讲解的截图）

石子合并

有限集中的最值：(n-1)(n-2)……*1,即n!个，暴力枚举肯定会超时

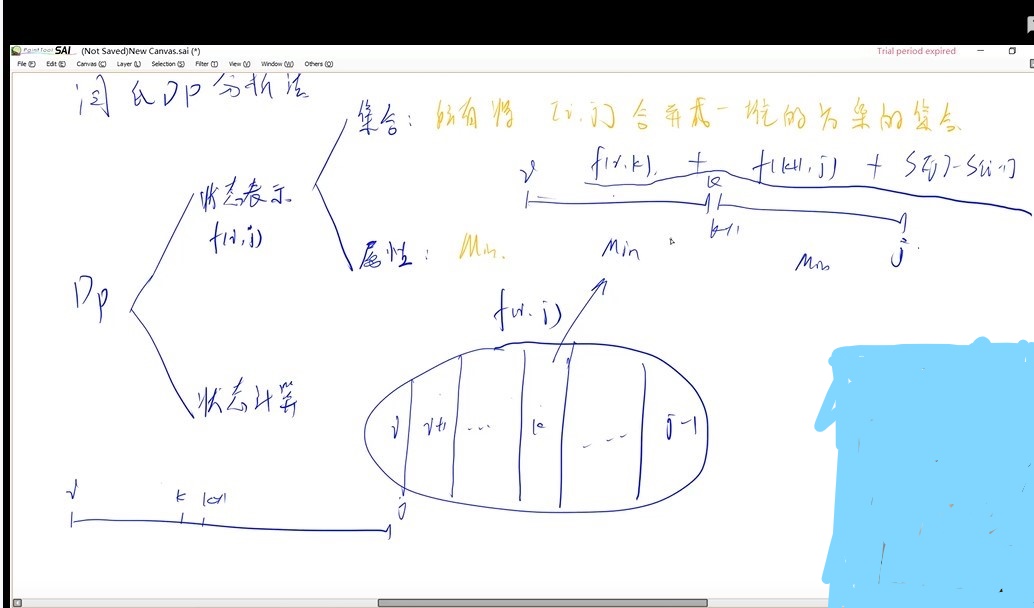
区间 DP 常用模版
所有的区间dp问题，第一维都是枚举区间长度，一般 len = 1 用来初始化，枚举从 len = 2 开始，第二维枚举起点 i （右端点 j 自动获得，j = i + len - 1）

for (int i = 1; i <= n; i++) {
    dp[i][i] = 初始值
}
for (int len = 2; len <= n; len++)           //区间长度，一般从2开始，1是它本身，区间为1不用合并，消耗为0
    for (int i = 1; i + len - 1 <= n; i++) { //枚举起点，i+len-1(右端点)<=n
        int j = i + len - 1;                 //区间终点
        for (int k = i; k < j; k++) {        //枚举分割点(区间)，构造状态转移方程
            dp[i][j] = max/min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
        }
    }

完整代码：

#include <iostream>
using namespace std;

const int N = 307;

int a[N], s[N];
int f[N][N];

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        s[i] += s[i - 1] + a[i];
    }
    // 区间 DP 枚举套路：长度+左端点 
    for (int len = 1; len < n; len ++) { // len表示i和j堆下标的差值
        for (int i = 1; i + len <= n; i ++) {
            int j = i + len; // 自动得到右端点
            f[i][j] = 1e8;
            for (int k = i; k <= j - 1; k ++) { // 必须满足k + 1 <= j
                f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
            }
        }
    }
    cout << f[1][n] << endl;
    return 0;
}

最长公共子序列

有限集中的最值：极端情况下，a和b的最长公共子序列是2^n个

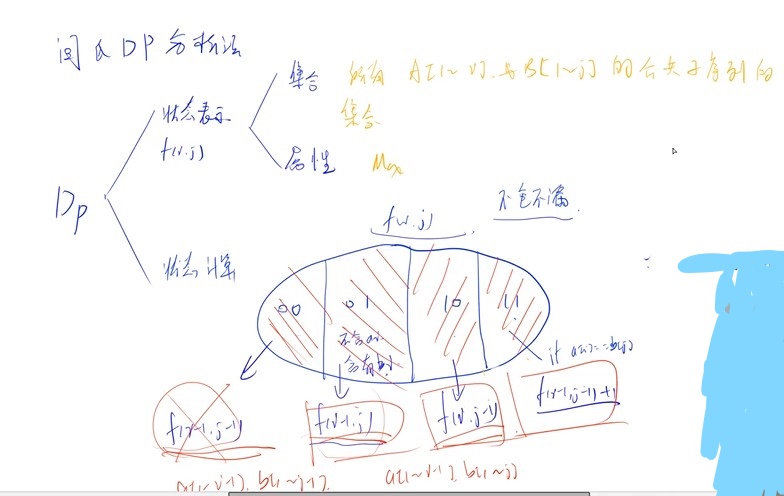
图片可通过链接在浏览器上打开

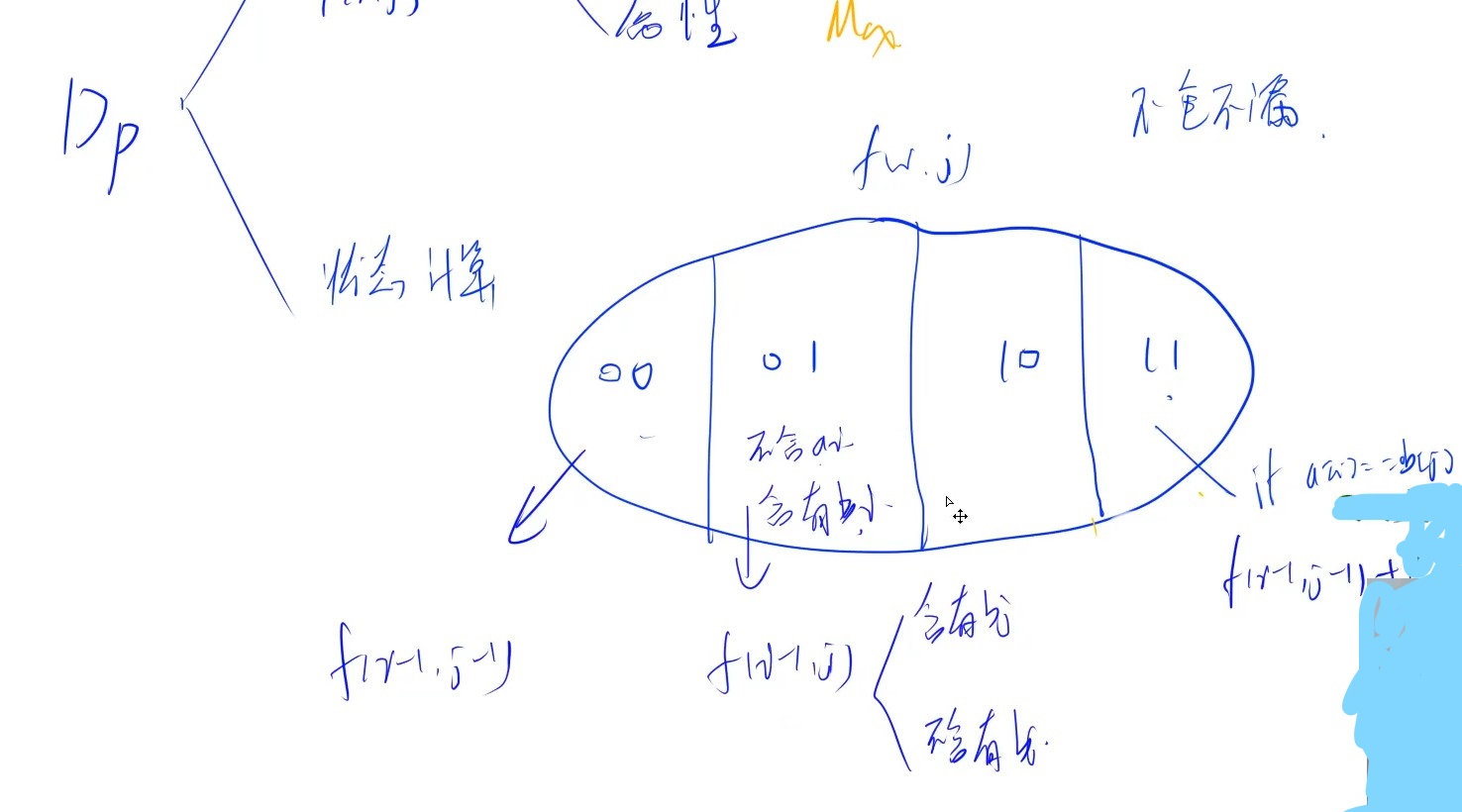
其中，00表示不含a[i],b[j]，01表示不含a[i],含有b[j]，10表示含有a[i],不含b[j];11表示都含有。
最后一个集合不一定有只有当a[i]==b[j]时，才有

注意：我们的状态表示中并未表明一定要选a[i],b[j]，所以可能会不选。因此要用“不重不漏”原则（此题是求数量）
所以f[i-1][j]有两种可能 ：1.含有b[j] 2.不含b[j]； 集合“01”是f[i-1][j]的子集，满足不重不漏原则，可用f[i-1][j]去覆盖“01”
同理f[i][j-1]也有两种可能：1.含有a[i] 2.不含a[i]; 集合“10”是f[i][j-1]的子集，满足不重不漏原则，可用f[i][j-1]去覆盖“11”
另外：”00”是被包含在“01”和“10”中的，所以最终只用看“01”，“10”，“11”（看状态表示可知道为什么）

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main() {
  cin >> n >> m >> a + 1 >> b + 1;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      if (a[i] == b[j]) {
        f[i][j] = f[i - 1][j - 1] + 1;
      } else {
        f[i][j] = max(f[i - 1][j], f[i][j - 1]);
      }
    }
  }
  cout << f[n][m] << '\n';
  return 0;
}