基本介绍

• 广度优先算法（又称宽度优先算法）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Breath First Search，简称 BFS

• $\rm{Dijkstra}$ 单源最短路径算法和 $\rm{Prim}$ 最小生成树算法都采用了宽度优先搜索类似的思想

• 广度优先算法的核心思想是：从初始节点开始，应用算符生成第一层节点，检查目标节点是否在这些后继节点中，若没有，再用产生式规则将所有第一层的节点逐一扩展，得到第二层节点，并逐一检查第二层节点中是否包含目标节点。若没有，再用算符逐一扩展第二层的所有节点，$\cdots$，如此依次扩展，检查下去，直到发现目标节点为止。即：
  1) 从某一顶点 $V_0$ 开始，先访问 $V_0$；
  2) 访问所有与 $V_0$ 相邻接的顶点 $V_1, V_2, \cdots, V_t$；
  3）依次访问与 $V_1, V_2, \cdots, V_t$ 相邻接的所有未曾访问过的顶点；
  4）循此以往，直到所有的顶点都被访问过为止。

如图，我们希望从 $A$ 城市走到 $H$ 城市，我们希望找出最短的路径，我们可以通过广度优先搜索的方式
从 $A$ 出发，$BCDF$ 的城市可以在 $1$ 步的距离内到达，$EGH$ 可以在 $2$ 步的距离到达

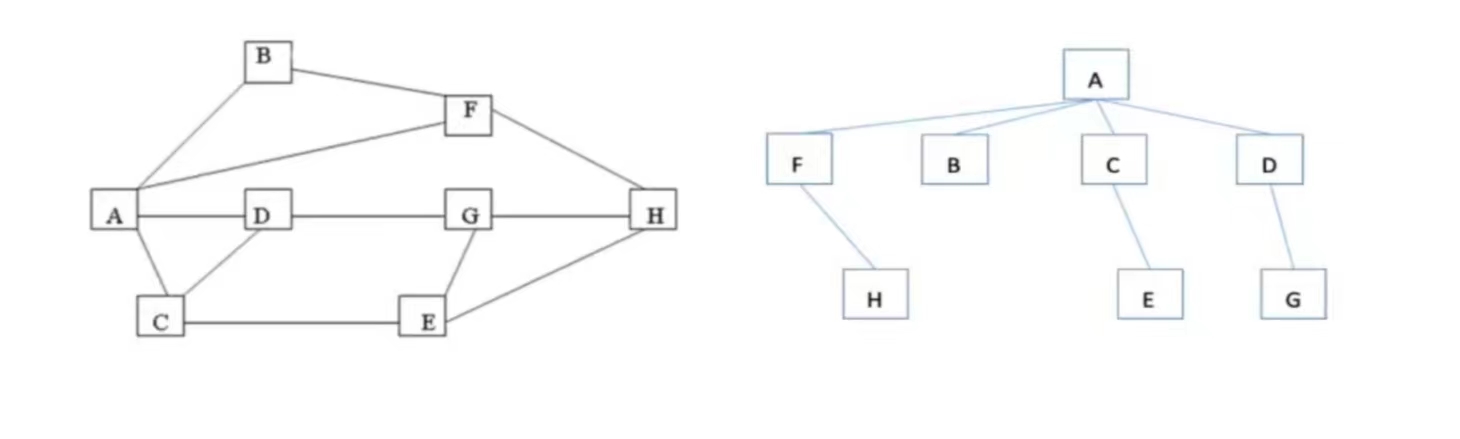
• 这种搜索的次序体现沿层次横向扩展的趋势，所以称之为广度优先搜索
• 适用于有明显的状态间的转移、状态能够方便存储的情况
• 适用于类似于 最少步数 的问题
• 一般使用队列实现

BFS 的基本框架：

void BFS()
    声明一个状态队列Q
    将初始状态 push 入 Q
    while Q 不为空
        取出 Q 的队首状态 v
        枚举 v 所有转移的状态 u
            如果 u 可以转移并且没有被访问过
                对 u 进行访问操作，并将其标记为已访问过
                将 u push 入 Q 的队尾  

例题1：迷宫

题目大意：在 $N \times N$ 的迷宫内，# 为墙，. 为路，s 为起点，e 为终点，一共 $4$ 个方向可以走。从左上角 $((0, 0)\ ‘s’)$ 位置处走到右下角 $((n-1, n-1) \ ‘e’)$ 位置处，可以走通则输出 YES，不可以走输出 NO

分析：

我们把一步到达的位置标记成 $A$，两步到达的位置标记为 $B$，三步到达的位置标记成 $C$
四步到达的位置标记成 $D$，如下图

sABC##.
A#CD...
BCD....
CD#....
D.#...#
###...#
......e

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using std::queue;
using std::string;
using P = std::pair<int, int>;

const int di[] = {0, 1, 0, -1};
const int dj[] = {1, 0, -1, 0};

void solve() {
    int n;
    cin >> n;

    vector<string> s(n);
    rep(i, n) cin >> s[i];

    vector used(n, vector<bool>(n));
    queue<P> q;
    used[0][0] = true;
    q.emplace(0, 0);
    while (q.size()) {
        auto [i, j] = q.front(); q.pop();
        rep(v, 4) {
            int ni = i+di[v], nj = j+dj[v];
            if (ni<0 or ni>=n or nj<0 or nj>=n or s[ni][nj] == '#') continue;
            if (used[ni][nj]) continue;
            used[ni][nj] = true;
            q.emplace(ni, nj);
        }
    }

    if (used[n-1][n-1]) puts("YES");
    else puts("NO");
}

int main() {
    int t;
    cin >> t;

    while (t--) solve();

    return 0;
}

例2. 八数码问题

在 $3×3$ 的棋盘上，摆有八个棋子，每个棋子上标有 $1$ 至 $8$ 的某一数字。棋盘中留有一个空格，空格用 $0$ 来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为 123804765），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

分析：

初始状态为 283104765 等价于表格 $1$
目标状态为 123804765 等价于表格 $2$

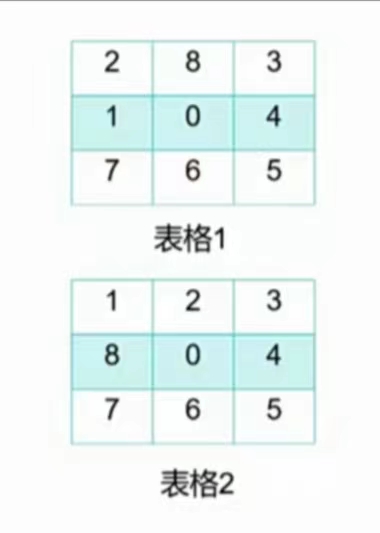
样例一共移动四步就可以完成

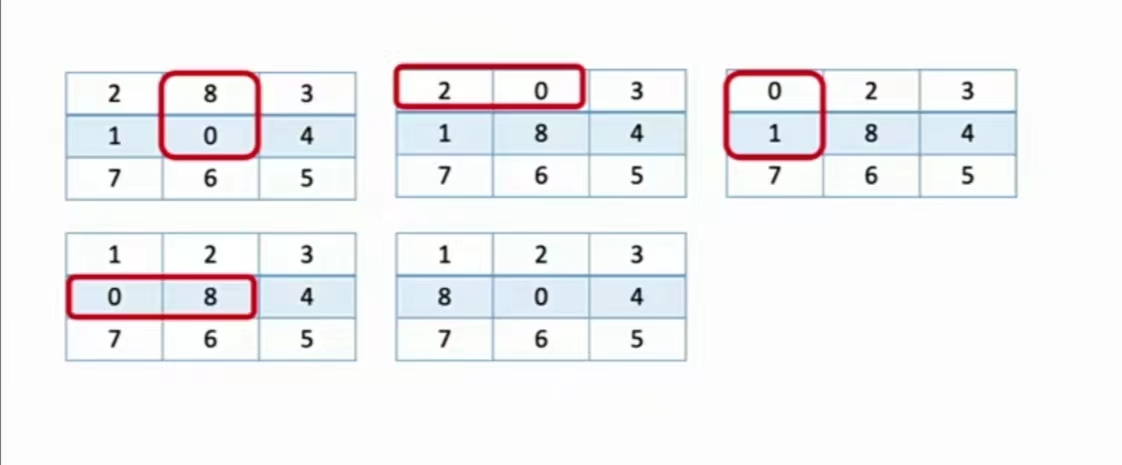
如何通过广度优先搜索找出最少的移动次数？

1. 初始状态
2. 目标状态
3. 状态之间的转移

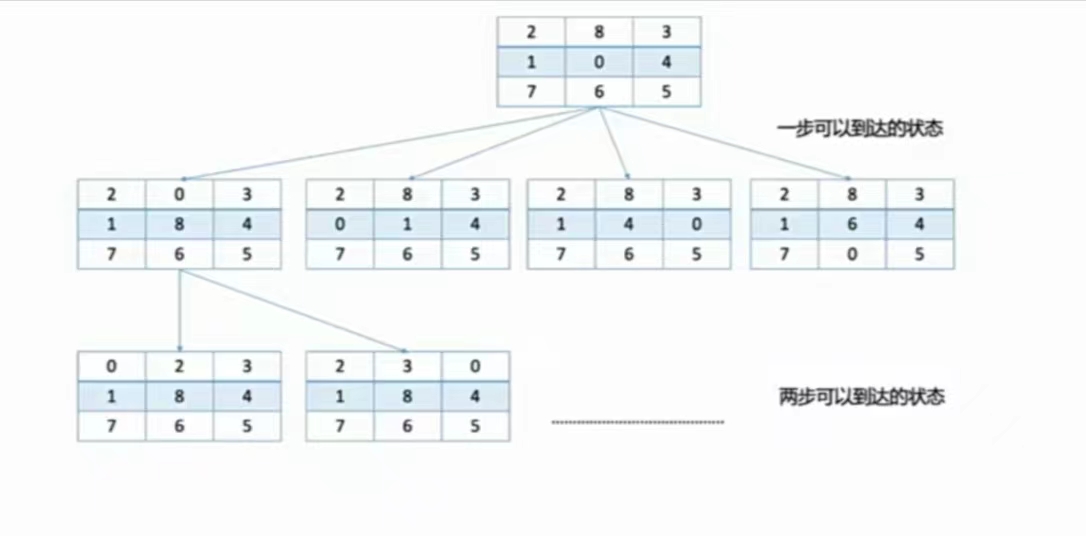
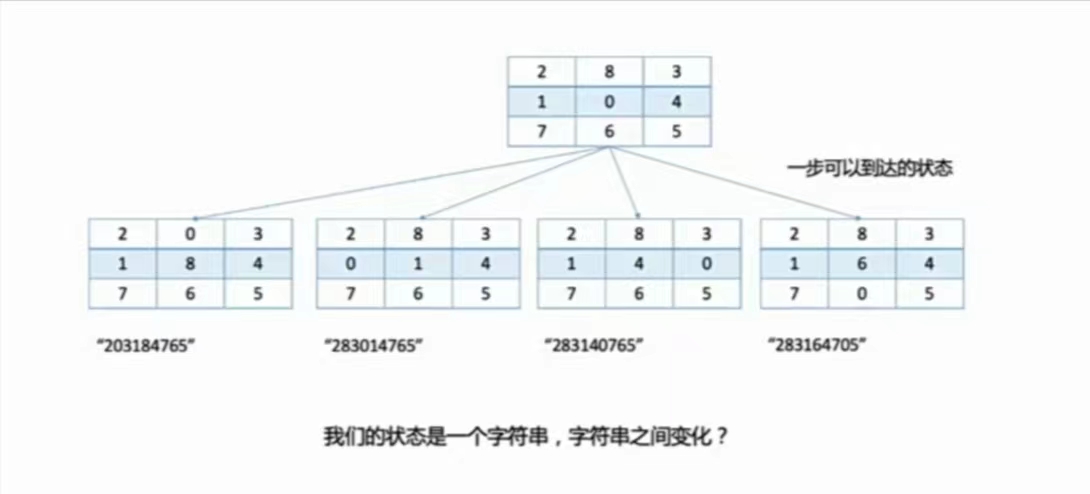
如果当前字符串是 $s$，p=s.find('0')，$p$ 就是 $0$ 的位置

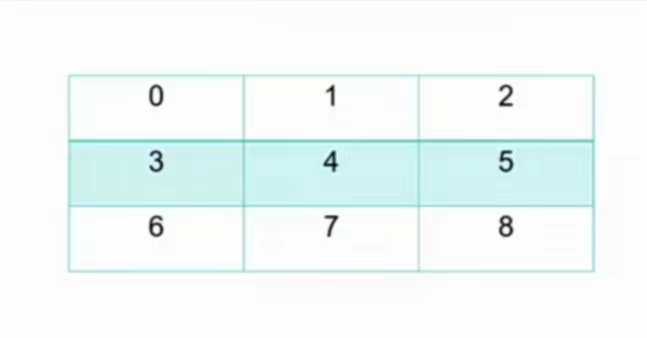
我们有四个方向可以交换
如果 $p \geqslant 3$， 那么 $p$ 和 $p-3$ （向上）的位置上的数字交换
如果 $p \% 3 \neq 0$，那么 $p$ 和 $p-1$（向左）的位置上的可以交换
如果 $p \leqslant 5$，那么 $p$ 和 $p+3$（向下）的位置上的数字可以交换
如果 $p \% 3 \neq 2$，那么 $p$ 和 $p+1$（向右）的位置上的数字可以交换

C++ 代码

#include <bits/stdc++.h>

using std::cin;
using std::cout;
using std::map;
using std::string;
using std::queue;

int main() {
    string init;
    cin >> init;

    map<string, int> dist;
    queue<string> q;
    dist[init] = 0;
    q.push(init);

    while (q.size()) {
        string s = q.front(); q.pop();
        if (s == "123804765") {
            cout << dist[s] << '\n';
            return 0;
        }

        int p = s.find('0');
        // 状态之间的扩展
        // up 向上扩展
        if (p >= 3) {
            string ns = s;
            std::swap(ns[p], ns[p-3]);
            if (!dist.count(ns)) {
                dist[ns] = dist[s] + 1;
                q.push(ns);
            }
        }

        // 向下
        if (p <= 5) {
            string ns = s;
            std::swap(ns[p], ns[p+3]);
            if (!dist.count(ns)) {
                dist[ns] = dist[s] + 1;
                q.push(ns);
            }
        }

        // 向左
        if (p % 3 != 0) {
            string ns = s;
            std::swap(ns[p], ns[p-1]);
            if (!dist.count(ns)) {
                dist[ns] = dist[s] + 1;
                q.push(ns);
            }
        }

        // 向右
        if (p % 3 != 2) {
            string ns = s;
            std::swap(ns[p], ns[p+1]);
            if (!dist.count(ns)) {
                dist[ns] = dist[s] + 1;
                q.push(ns);
            }
        }
    }

    return 0;
}

例3. 幅優先探索

一个大小为 $n\times m$ 的迷宫，你可以往上下左右任意方向移动 $1$ 步，求最少需要多少步才能走出迷宫。

迷宫中 . 表示空地，# 表示墙壁，移动中只能穿过空地，不能穿墙。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::string;
using std::vector;
using std::queue;
using P = std::pair<int, int>;

const int dx[4] = {0, 1, 0, -1};
const int dy[4] = {1, 0, -1, 0};

int main() {
    int n, m;
    cin >> n >> m;

    int sy, sx, ty, tx;
    cin >> sy >> sx >> ty >> tx;
    --sy; --sx; --ty; --tx;

    vector<string> s(n);
    rep(i, n) cin >> s[i];

    vector dist(n, vector<int>(m, -1));
    queue<P> q;
    q.emplace(sy, sx);
    dist[sy][sx] = 0;
    while (q.size()) {
        auto [y, x] = q.front(); q.pop();
        rep(v, 4) {
            int ny = y+dy[v], nx = x+dx[v];
            if (s[ny][nx] == '#' or ~dist[ny][nx]) continue;
            dist[ny][nx] = dist[y][x] + 1;
            q.emplace(ny, nx);
        }
    }

    int ans = dist[ty][tx];
    cout << ans << '\n';

    return 0;
}

例4. Tour

只需检验任意两点是否连通即可，具体可以通过跑 $n$ 次 $\mathsf{BFS}$ 来实现。

代码实现：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using std::queue;

int main() {
    int n, m;
    cin >> n >> m;

    vector<vector<int>> to(n);
    rep(i, m) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
    }

    int ans = 0;
    rep(sv, n) {
        queue<int> q;
        vector<int> used(n);
        used[sv] = 1;
        ++ans;
        q.push(sv);
        while (q.size()) {
            int v = q.front(); q.pop();
            for (int u : to[v]) {
                if (used[u]) continue;
                ++ans;
                used[u] = 1;
                q.push(u);
            }
        }
    }

    cout << ans << '\n';

    return 0;
}

例5. Shortest Path 1

给定 $N$ 个点 $M$ 条边的无向图。每个点的编号分别为 $1 \sim N$，第 $i$ 条边连接点 $A_i$ 和点 $B_i$ 。
对于 $1 \sim N$ 之间的所有整数 $k$，要求回答以下问题：

• 求点 $1$ 到点 $k$ 的最短路，若不可能到达点 $k$ 则输出 -1 。

限制：

• $1 \leqslant N \leqslant 10^5$
• $0 \leqslant M \leqslant \min(10^5, \frac{N(N-1)}{2})$
• $1 \leqslant A_i < B_i \leqslant N$
• 不存在重边和自环

C++ 代码

#include <bits/extc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;

    vector<vector<int>> to(n);
    rep(i, m) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector<int> dist(n, -1);
    queue<int> q;
    dist[0] = 0;
    q.push(0);
    while (q.size()) {
        int v = q.front(); q.pop();
        for (int u : to[v]) {
            if (dist[u] == -1) {
                dist[u] = dist[v]+1;
                q.push(u);
            }
        }
    }

    rep(i, n) cout << dist[i] << '\n';

    return 0;
}

例6. 网格中的最短路径

记 dist(x, y, z) 表示玩家走到 $(x, y)$ 时经过 $z$ 个障碍物的最短路

C++ 代码

const int dx[4] = {0, 1, 0, -1};
const int dy[4] = {1, 0, -1, 0};
class Solution {
public:
    int shortestPath(vector<vector<int>>& g, int k) {
        int n = g.size(), m = g[0].size();
        const int INF = 1001001001;
        k = min(k, max(0, n+m-3));
        vector dist(n, vector<vector<int>>(m, vector<int>(k+1, INF)));
        dist[0][0][0] = 0;
        queue<array<int, 3>> q;
        q.push({0, 0, 0});
        while (q.size()) {
            auto [x, y, z] = q.front(); q.pop();
            int d = dist[x][y][z];
            if (x == n-1 and y == m-1) return d;
            for (int v = 0; v < 4; ++v) {
                int nx = x+dx[v], ny = y+dy[v];
                if (nx < 0 or nx >= n or ny < 0 or ny >= m) continue;
                int nz = z+g[x][y];
                if (nz <= k and dist[nx][ny][nz] > d+1) {
                    dist[nx][ny][nz] = d+1;
                    q.push({nx, ny, nz});
                }
            }
        }
        return -1;
    }
};

例7. 目的地的最短路径

C++ 代码

using P = pair<int, int>;
class Solution {
public:
    /**
     * @param targetMap: 
     * @return: nothing
     */
    const int dx[4] = {0, 1, 0, -1};
    const int dy[4] = {1, 0, -1, 0};
    int shortestPath(vector<vector<int>> &g) {
        int n = g.size(), m = g[0].size();
        const int INF = 1001001001;
        vector<vector<int>> dist(n, vector<int>(m, INF));
        dist[0][0] = 0;
        queue<P> q;
        q.emplace(0, 0);
        while (q.size()) {
            auto [x, y] = q.front(); q.pop();
            int d = dist[x][y];
            if (g[x][y] == 2) return d;
            for (int v = 0; v < 4; ++v) {
                int nx = x+dx[v], ny = y+dy[v];
                if (nx < 0 or nx >= n or ny < 0 or ny >= m or g[nx][ny] == 1) continue;
                if (dist[nx][ny] != INF) continue;
                dist[nx][ny] = d+1;
                q.emplace(nx, ny);
            }
        }
        return -1;
    }
};

例8. RPG跑腿任务

本题难度中等，$\operatorname{BFS}$ 求最短路，需要注意走到和 $M$ 相邻的格子就算到达。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using P = pair<int, int>;

const int di[] = {-1, 0, 1, 0};
const int dj[] = {0, 1, 0, -1};

int main() {
    int r, c;
    cin >> r >> c;

    vector<string> s(r);
    rep(i, r) cin >> s[i];

    set<P> st;
    rep(i, r)rep(j, c) {
        if (s[i][j] == 'M') {
            if (i-1 >= 0 and s[i-1][j] != 'T') st.emplace(i-1, j);
            if (i+1 < r and s[i+1][j] != 'T') st.emplace(i+1, j);
            if (j-1 >= 0 and s[i][j-1] != 'T') st.emplace(i, j-1);
            if (j+1 < c and s[i][j+1] != 'T') st.emplace(i, j+1);
        }
    }

    const int INF = 1001001001;
    vector<vector<int>> dist(r, vector<int>(c, INF));
    queue<P> q;
    rep(i, r)rep(j, c) {
        if (s[i][j] == 'S') {
            q.emplace(i, j);
            dist[i][j] = 0;
        }
    }
    while (q.size()) {
        auto [i, j] = q.front(); q.pop();
        if (st.count(P(i, j))) {
            cout << dist[i][j] << '\n';
            return 0;
        }
        rep(v, 4) {
            int ni = i+di[v], nj = j+dj[v];
            if (ni < 0 or ni >= r or nj < 0 or nj >= c) continue;
            if (s[ni][nj] == 'T') continue;
            if (dist[ni][nj] != INF) continue;
            dist[ni][nj] = dist[i][j]+1;
            q.emplace(ni, nj);
        }
    }

    puts("-1");

    return 0;
}