满足条件的01序列

对于该题，用到了卡特兰数（有非常多的应用）即

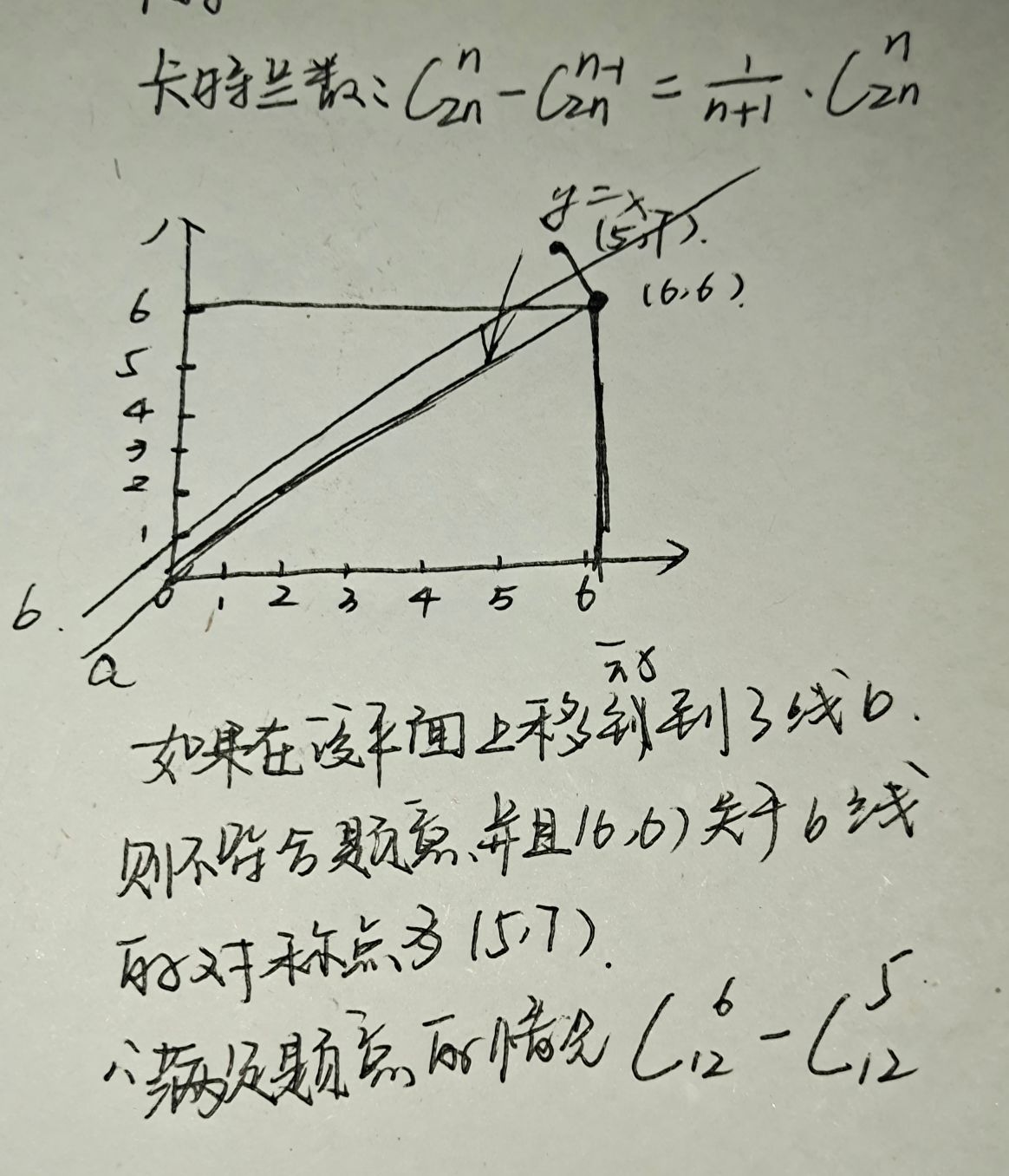
对于该题涉及到求逆元，b * x = 1(mod m)因为mod=1e9+7是一个质数，所以求逆元可以通过快速幂
也就是费马小定理来求解 ksm(i,mod-2)
如果mod不是一个质数，则可以通过扩展欧几里得算法来求解，通过比较时间，扩展欧几里得方法
比快速幂方法快非常多

欧几里得求逆元代码：

#include<iostream>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
int n;
int  exgcd(int a,int b,int &x,int &y){

    if(!b){

        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y=y - (ll)a / b * x % mod;
    return d;
}
int main(){

    cin>>n;
    ll res=1;
    for(int i=2*n;i>n;i--)
    res=res*i%mod;
    int x,y;
    for(int i=1;i<=n;i++){
        int d=exgcd(i,mod,x,y);

        res=res*(x%mod+mod)%mod;
    }
    exgcd(n+1,mod,x,y);
    int f=res*(x%mod+mod)%mod;
    cout<<f;

    return 0;
}

快速幂求逆元代码：

#include<iostream>
using namespace std;
typedef long long ll;
ll mod=1e9+7;

ll ksm(ll a,ll b ){
    ll res=1;
    while(b){
        if(b&1){
            res=res*a%mod;
        }
        b=b>>1;
        a=a*a%mod;
    }
    return res;
}
int main(){
    int n;
    cin>>n;
    ll res=1;
    for(int i=2*n,j=n;i>n;j--,i--){
        res=res*i%mod;
        res=res*ksm(j,mod-2)%mod;
    }

    res=res*ksm(n+1,mod-2)%mod;
    cout<<res;
    return 0;
}

同时在求解阶乘值时，上边两个代码均使用的是阶乘式化简后进行求值，
另外一种方法是预处理递推的方式，
这两种方法在本题中差别还是很大的，预处理方式的时间明显多于以上两个代码
对于这两种方法的选取在前四个组合数中也应该明确，什么时候使用会更加节约时间，
y总给的算法模板中耗时最少

预处理递推代码：

#include<iostream>
using namespace std;
typedef long long ll;
ll mod=1e9+7;
const int m=200010;//注意这里是2*n
ll fact[m];
ll infact[m];
ll ksm(ll a,ll b){
    ll res=1;
    while(b){
        if(b&1)
        res=res*a%mod;
        a=a*a%mod;
        b=b>>1;
    }
    return res;
}
int main(){
    int n;
    cin>>n;
    fact[0]=infact[0]=1;
    for(int i=1;i<m;i++){
        infact[i]=infact[i-1]*ksm(i,mod-2)%mod;
        fact[i]=fact[i-1]*i%mod;
    }


    ll res;
    res=fact[2*n]*infact[n]%mod*infact[n]%mod*ksm(n+1,mod-2)%mod;
    cout<<res;
    return 0;
}