(1)快速幂
给定 n 组 ai,bi,pi,对于每组数据,求出 abiimodpi 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含三个整数 ai,bi,pi。
输出格式
对于每组数据,输出一个结果,表示 abiimodpi 的值。
每个结果占一行。
数据范围
1≤n≤100000,
1≤ai,bi,pi≤2×109
输入样例:
2
3 2 5
4 3 9
输出样例:
4
1
代码:
#include<iostream>
using namespace std;
typedef long long LL;
LL qmi(int a, int k, int p)
{
LL res=1;
while(k)
{
if(k&1)res=res*a%p;
k>>=1; //k除以2
a=(LL)a*a%p;
}
return res;
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int a,b,p;
scanf("%d%d%d",&a,&b,&p);
printf("%lld\n",qmi(a,b,p));
}
return 0;
}
(2)快速幂求逆元
给定 n 组 ai,pi,其中 pi 是质数,求 ai 模 pi 的乘法逆元,若逆元不存在则输出 impossible。
注意:请返回在 0∼p−1 之间的逆元。
乘法逆元的定义
若整数 b,m 互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(modm),则称 x 为 b 的模 m 乘法逆元,记为 b−1(modm)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,bm−2 即为 b 的乘法逆元。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个数组 ai,pi,数据保证 pi 是质数。
输出格式
输出共 n 行,每组数据输出一个结果,每个结果占一行。
若 ai 模 pi 的乘法逆元存在,则输出一个整数,表示逆元,否则输出 impossible。
数据范围
1≤n≤105,
1≤ai,pi≤2∗109
输入样例:
3
4 3
8 5
6 3
输出样例:
1
2
impossible

代码:
#include<iostream>
using namespace std;
typedef long long LL;
LL qmi(int a, int k, int p)
{
LL res=1;
while(k)
{
if(k&1)res=res*a%p;
k>>=1; //k除以2
a=(LL)a*a%p;
}
return res;
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int a,p;
scanf("%d%d",&a,&p);
if (a % p == 0) puts("impossible");
else printf("%lld\n", qmi(a, p - 2, p));
}
return 0;
}
(3)序列的第k个数
BSNY 在学等差数列和等比数列,当已知前三项时,就可以知道是等差数列还是等比数列。
现在给你 整数 序列的前三项,这个序列要么是等差序列,要么是等比序列,你能求出第 k 项的值吗。
如果第 k 项的值太大,对其取模 200907。
输入格式
第一行一个整数 T,表示有 T 组测试数据;
对于每组测试数据,输入前三项 a,b,c,然后输入 k。
输出格式
对于每组数据,输出第 k 项取模 200907 的值。
数据范围
1≤T≤100,
1≤a≤b≤c≤109,
1≤k≤109
输入样例:
2
1 2 3 5
1 2 4 5
输出样例:
5
16
代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long LL;
const int mod = 200907;
LL qmi(int a,int k)
{
LL res=1;
while(k)
{
if(k&1)res=res*a%mod;
k>>=1;
a=(LL)a*a%mod;
}
return res;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
int a, b, c, k;
cin >> a >> b >> c >> k;
if (a + c == b * 2) cout << (a + (b - a) * (LL)(k - 1)) % mod << endl;
else cout << (LL)a * qmi(b / a, k - 1) % mod << endl;
}
return 0;
}
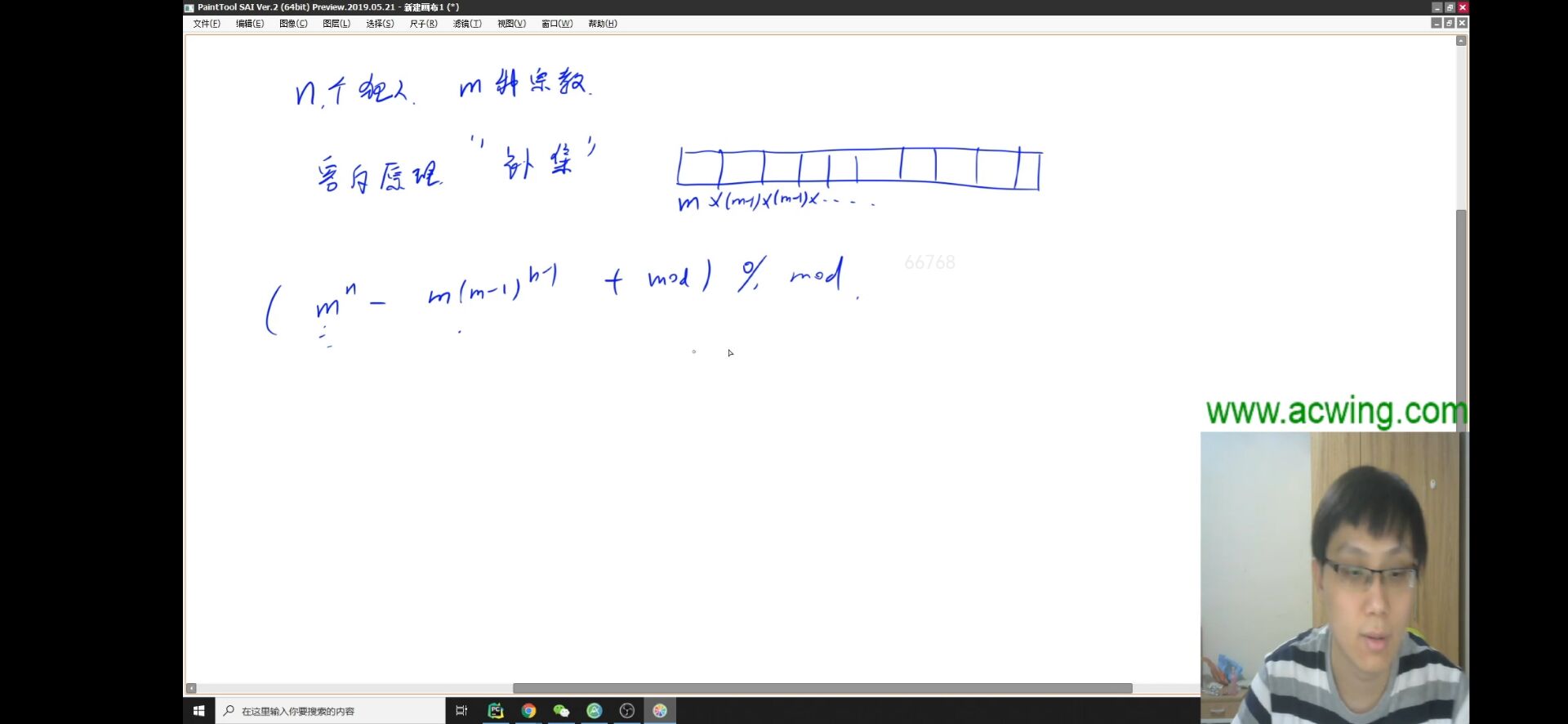
(4)越狱
监狱有连续编号为 1 到 n 的 n 个房间,每个房间关押一个犯人。
有 m 种宗教,每个犯人可能信仰其中一种。
如果相邻房间的犯人信仰的宗教相同,就可能发生越狱。
求有多少种状态可能发生越狱。
输入格式
共一行,包含两个整数 m 和 n。
输出格式
可能越狱的状态数,对 100003 取余。
数据范围
1≤m≤108,
1≤n≤1012
输入样例:
2 3
输出样例:
6
样例解释
所有可能的 6 种状态为:(000)(001)(011)(100)(110)(111)。
代码:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int mod = 100003;
int qmi(int a, LL k)
{
LL res = 1;
while (k)
{
if (k & 1) res = res * a % mod;
a = (LL)a * a % mod;
k >>= 1;
}
return res;
}
int main()
{
int m;
LL n;
cin >> m >> n;
cout << (qmi(m, n) - (LL)m * qmi(m - 1, n - 1) % mod + mod) % mod << endl;
return 0;
}
(5)约数之和
假设现在有两个自然数 A 和 B,S 是 AB 的所有约数之和。
请你求出 Smod9901 的值是多少。
输入格式
在一行中输入用空格隔开的两个整数 A 和 B。
输出格式
输出一个整数,代表 Smod9901 的值。
数据范围
0≤A,B≤5×107
输入样例:
2 3
输出样例:
15
注意: A 和 B 不会同时为 0。

代码:
#include<iostream>
#include<unordered_map>
using namespace std;
typedef long long LL;
const int mod = 9901;
int A, B;
//保存质因子以及出现的次数
unordered_map<int, int> primes;
//试除法质因子分解
void divide(int n) {
for(int i = 2; i <= n / i; i++) {
if(n % i == 0) {
while(n % i == 0) {
primes[i]++;
n /= i;
}
}
}
if(n > 1) {
primes[n]++;
}
}
//快速幂
int qmid(int a, int b) {
int res = 1;
while(b) {
if(b & 1) res = (LL)res * a % mod;
a = (LL)a * a % mod;
b >>= 1;
}
return res;
}
int main(){
cin >> A >> B;
//对A分解质因子
divide(A);
int res = 1;
for(auto it : primes) {
//p是质因子,k是质因子的次数
int p = it.first, k = it.second * B;
// res要乘上每一项, 注意这里是k + 1
if((p - 1) % mod == 0) {
//不存在逆元,由于p - 1的是mod 的倍数, 故p % mod = 1
//所以1 + p + ... + p^k每个数%mod 都是1,共k + 1个数,总就是k + 1
res = (LL)res * (k + 1) % mod;
}
else{
res = (LL)res * (qmid(p, k + 1) - 1) % mod * qmid(p - 1, mod - 2) % mod;
}
}
if(!A) res = 0;
cout << (res % mod + mod ) % mod << endl;
return 0;
}
总结:分母p-1是mod的倍数,不存在逆元,这时直接乘(1+p+…pk)%mod, 即 k+1
分母p-1不是mod的倍数,存在逆元,这是需要用快速幂求分子,再用快速幂求分母的逆元,两者相乘就得到了每一项
(6)64位整数乘法
include[HTML_REMOVED]
include[HTML_REMOVED]
include[HTML_REMOVED]
include[HTML_REMOVED]
using namespace std;
typedef long long ll;
int main()
{
ll a,b,p;
ll res=0;
cin>>a>>b>>p;
while(b)
{
if(b&1)
res=(res+a)%p;
b>>=1;
a=2*a%p;
}
cout<<res;
return 0;
}

