(1)约数个数
给定 n 个正整数 ai，请你输出这些数的乘积的约数个数，答案对 109+7 取模。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出一个整数，表示所给正整数的乘积的约数个数，答案需对 109+7 取模。

数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：
3
2
6
8
输出样例：
12
难度：简单
时/空限制：1s / 64MB
总通过数：12342
总尝试数：22036
来源：模板题
算法标签

代码

#include<iostream>
#include<map>
#include<vector>
#include<algorithm>

using namespace std;
typedef long long ll;

const int N = 110, mod = 1e9 + 7;
int main()
{
    int n;
    cin>>n;
    map<int, int> p;
    while(n--)
    {
        int k;
        scanf("%d",&k);
        for(int i=2;i<=k/i;i++)
        {
            while(k%i==0)
            {
                k/=i;
                p[i]++;
            }
        }
          if (k > 1) p[k] ++ ;
    }
    ll res = 1;
    for(map<int,int>::iterator q= p.begin();q!=p.end();q++)
    {
        res=res*(q->second+1)%mod; 
    }
        cout << res << endl;

    return 0;
}

(2) 轻拍牛头
今天是贝茜的生日，为了庆祝自己的生日，贝茜邀你来玩一个游戏．

贝茜让 N 头奶牛（编号 1 到 N）坐成一个圈。

除了 1 号与 N 号奶牛外，i 号奶牛与 i−1 号和 i+1 号奶牛相邻，N 号奶牛与 1 号奶牛相邻。

农夫约翰用很多纸条装满了一个桶，每一张纸条中包含一个 1 到 1000000 之间的数字。

接着每一头奶牛 i 从桶中取出一张纸条，纸条上的数字用 Ai 表示。

所有奶牛都选取完毕后，每头奶牛轮流走上一圈，当走到一头奶牛身旁时，如果自己手中的数字能够被该奶牛手中的数字整除，则拍打该牛的头。

牛们希望你帮助他们确定，每一头奶牛需要拍打的牛的数量。

即共有 N 个整数 A1,A2,…,AN，对于每一个数 Ai，求其他的数中有多少个是它的约数。

输入格式
第一行包含整数 N。

接下来 N 行，每行包含一个整数 Ai。

输出格式
共 N 行，第 i 行的数字为第 i 头牛需要拍打的牛的数量。

数据范围
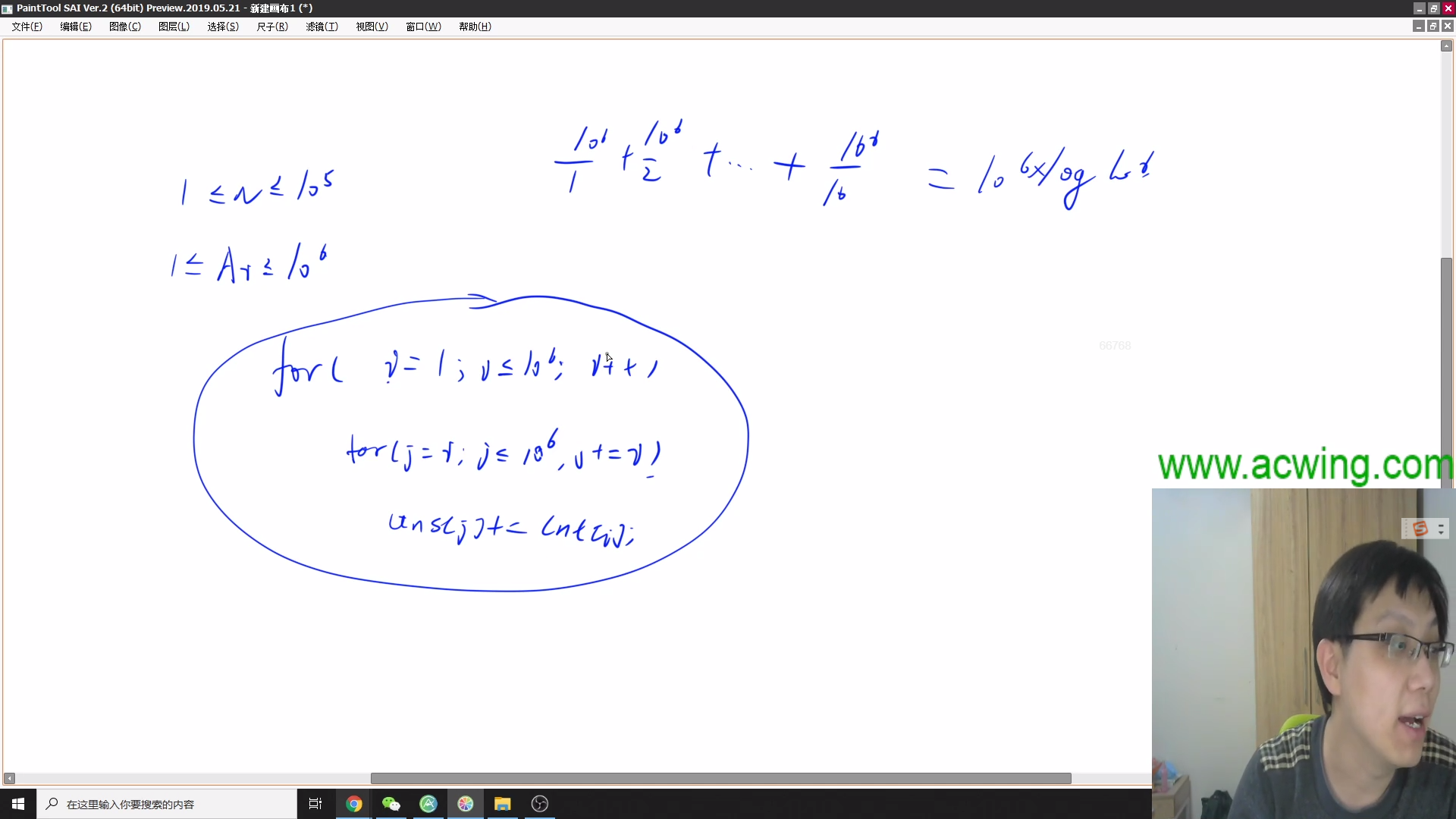
1≤N≤105,
1≤Ai≤106
输入样例：
5
2
1
2
3
4
输出样例：
2
0
2
1
3

代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

using namespace std;

const int N = 1e6+10;
int n;
int cnt[N];
int a[N];
int s[N];

int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
        cnt[a[i]]++;
    }

    for(int i=1;i<N;i++)
    {
        for(int j=i;j<N;j+=i)
        {
            s[j]+=cnt[i];
        }
    }

    for(int i=0;i<n;i++)printf("%d\n",s[a[i]]-1);

    return 0;
}

(3)樱花
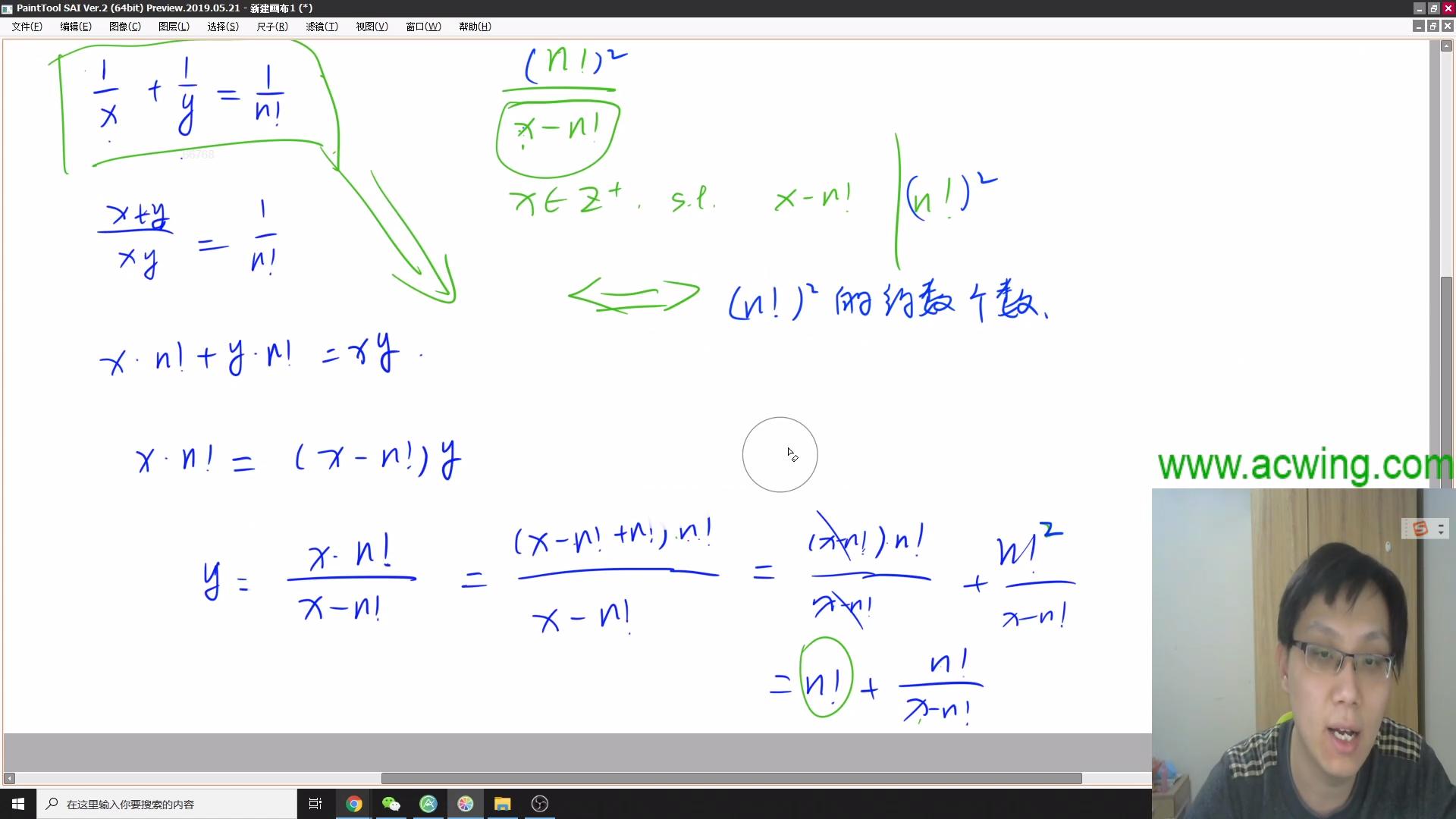
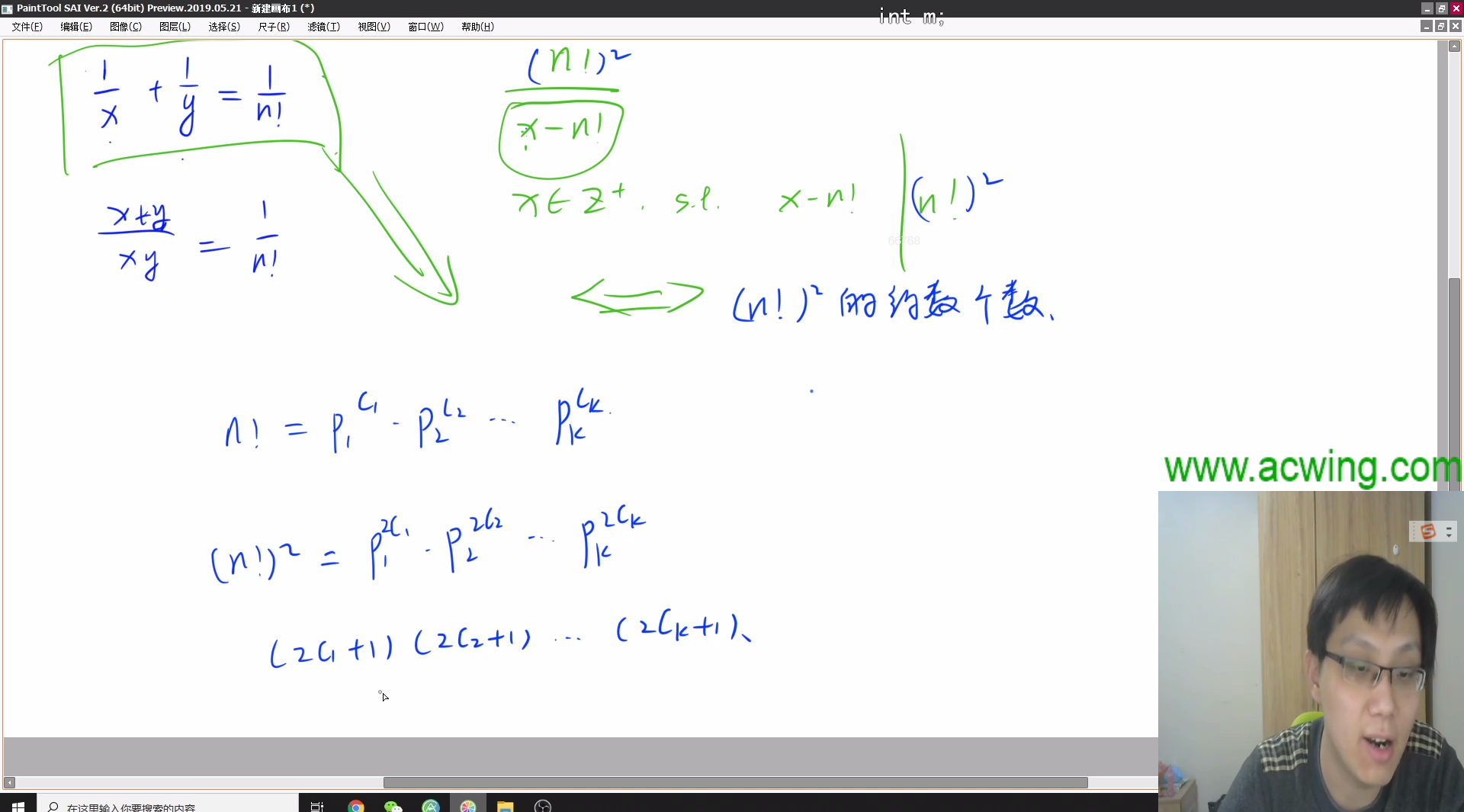
给定一个整数 n，求有多少正整数数对 (x,y) 满足 1x+1y=1n!。

输入格式
一个整数 n。

输出格式
一个整数，表示满足条件的数对数量。

答案对 109+7 取模。

数据范围
1≤n≤106
输入样例：
2
输出样例：
3
样例解释
共有三个数对 (x,y) 满足条件，分别是 (3,6),(4,4),(6,3)。


代码：

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10, mod = 1e9 + 7;

int primes[N], cnt;
bool st[N];

void init(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main()
{
    int n;
    cin >> n;

    init(n);

    int res = 1;
    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        int s = 0;
        for (int j = n; j; j /= p) s += j / p;
        res = (LL)res * (2 * s + 1) % mod;
    }

    cout << res << endl;


    return 0;
}

（4）反素数
对于任何正整数 x，其约数的个数记作 g(x)，例如 g(1)=1、g(6)=4。

如果某个正整数 x 满足：对于任意的小于 x 的正整数 i，都有 g(x)>g(i)，则称 x 为反素数。

例如，整数 1，2，4，6 等都是反素数。

现在给定一个数 N，请求出不超过 N 的最大的反素数。

输入格式
一个正整数 N。

输出格式
一个整数，表示不超过 N 的最大反素数。

数据范围
1≤N≤2∗109
输入样例：
1000
输出样例：
840
难度：中等
时/空限制：1s / 64MB
总通过数：2682
总尝试数：4298
来源：《算法竞赛进阶指南》, HAOI2007
算法标签

代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

using namespace std;

int n;

/*
第一个参数：代表第几个质数因子
第二个参数：代表第几个质数因子最大是有多少几个
第三个参数：代表此时的数是多少
第四个参数：代表第几个质数因子有几个
*/
int maxd;   //最大的约数个数
int number; //此时这个数是多少
typedef long long LL;

int primes[9] = {2, 3, 5, 7, 11, 13, 17, 19, 23};

void dfs(int u, int last, int p, int s)
{
    if(s>maxd||s==maxd&&p<number)
    {
        maxd=s;
        number=p;
    }
    if(u==9)return;

    for(int i=1;i<=last;i++)
    {
        if((LL)p*primes[u]>n)break;
        p*=primes[u];
        dfs(u+1,i,p,s*(i+1));
    }
}

int main()
{
    cin>>n;
    dfs(0,30,1,1);
    cout<<number;
    cout<<maxd; //约数个数最多的数有1600  2的三十一次方-1内
    return 0;
}

（5）约数之和
给定 n 个正整数 ai，请你输出这些数的乘积的约数之和，答案对 109+7 取模。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出一个整数，表示所给正整数的乘积的约数之和，答案需对 109+7 取模。

数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：
3
2
6
8
输出样例：
252
难度：简单
时/空限制：1s / 64MB
总通过数：10590
总尝试数：17211
来源：模板题
算法标签
代码

#include<iostream>
#include<map>
#include<vector>
#include<algorithm>

using namespace std;
typedef long long ll;

const int N = 110, mod = 1e9 + 7;
int main()
{
        map<int, int> p;
        int k;
        scanf("%d",&k);
        for(int i=2;i<=k/i;i++)
        {
            while(k%i==0)
            {
                k/=i;
                p[i]++;
                }
        }
          if (k > 1) p[k] ++ ;

    ll res = 1;
    for(map<int,int>::iterator q= p.begin();q!=p.end();q++)
    {
        ll a=q->first,b=q->second;
        ll t= 1;
        while(b--)t=(t * a + 1) % mod;
        res = res * t % mod;
    }
        cout << res << endl;

    return 0;
}

(6)最大公约数
给定 n 对正整数 ai,bi，请你求出每对数的最大公约数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数对 ai,bi。

输出格式
输出共 n 行，每行输出一个整数对的最大公约数。

数据范围
1≤n≤105,
1≤ai,bi≤2×109
输入样例：
2
3 6
4 6
输出样例：
3
2
代码

#include<iostream>
using namespace std;

int gcb(int a,int b)
{
    return b?gcb(b,a%b):a;
}
int main()
{
    int n;
    scanf("%d",&n);
    int a,b;
    while(n--)
    {
        scanf("%d%d",&a,&b);
        printf("%d\n",gcb(a,b));
    }
    return 0;
}

(7)Hankson的趣味题
Hanks 博士是 BT（Bio-Tech，生物技术）领域的知名专家，他的儿子名叫 Hankson。

现在，刚刚放学回家的 Hankson 正在思考一个有趣的问题。

今天在课堂上，老师讲解了如何求两个正整数 c1 和 c2 的最大公约数和最小公倍数。

现在 Hankson 认为自己已经熟练地掌握了这些知识，他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”，这个问题是这样的：

已知正整数 a0,a1,b0,b1，设某未知正整数 x 满足：

x 和 a0 的最大公约数是 a1；
x 和 b0 的最小公倍数是 b1。
Hankson 的“逆问题”就是求出满足条件的正整数 x。

但稍加思索之后，他发现这样的 x 并不唯一，甚至可能不存在。

因此他转而开始考虑如何求解满足条件的 x 的个数。

请你帮助他编程求解这个问题。

输入格式
输入第一行为一个正整数 n，表示有 n 组输入数据。

接下来的 n 行每行一组输入数据，为四个正整数 a0，a1，b0，b1，每两个整数之间用一个空格隔开。

输入数据保证 a0 能被 a1 整除，b1 能被 b0 整除。

输出格式
输出共 n 行。

每组输入数据的输出结果占一行，为一个整数。

对于每组数据：若不存在这样的 x，请输出 0；

若存在这样的 x，请输出满足条件的 x 的个数；

数据范围
1≤n≤2000,
1≤a0,a1,b0,b1≤2∗109
输入样例：
2
41 1 96 288
95 1 37 1776
输出样例：
6
2
难度：中等
时/空限制：0.3s / 64MB
总通过数：2180
总尝试数：6341
来源：《算法竞赛进阶指南》, NOIP2009提高组
算法标签
代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>

using namespace std;

typedef long long LL;
const int N = 50010;

int primes[N],cnt;
struct Factor
{
    int p, s;   //每个质数,分别出现几次

}factor[10];int fcnt;

bool st[N];
int dividor[1601], dcnt;

void init(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!st[i])primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)break;
        }
    }
}

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

void dfs(int u,int p)
{
    if(u==fcnt)
    {
        dividor[dcnt++]=p;
        return ;
    }
    for(int i=0;i<=factor[u].s;i++)
    {
        dfs(u+1,p);
        p*=factor[u].p;
    }
}

int main()
{
    init(N-1);
    int n;
    cin>>n;
    while(n--)
    {
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        fcnt=0;     //有那几个质数
        int t = d;  //将d分解质因数，求它的所有约数
        for(int i=0;primes[i]<=t/primes[i];i++)
        {
            int p=primes[i];
            if(t%p==0)
            {
                int s=0;
                while(t%p==0)
                {
                    s++;
                    t/=p;
                }
                factor[fcnt++]={p,s};
            }
        }
        if (t > 1) factor[fcnt ++ ] = {t, 1};

        dcnt=0; //约数个数
        dfs(0,1);
        int res = 0;
        for (int i = 0; i < dcnt; i ++ )
        {
            int x = dividor[i];
            if (gcd(a, x) == b && (LL)c * x / gcd(c, x) == d) res ++ ;
        }

        cout << res << endl;
    }
    return 0;
}

最小公倍数=两数的乘积/最大公约(因)数
（8）三个数的最小公倍数
链接：https://ac.nowcoder.com/acm/contest/26791/D
来源：牛客网

题目描述
小饼干有次过河发现河边有三种载客量分别为a,b,c的船，小饼干来了兴致，他想知道至少有多少人才能不管选哪种船都能刚好坐满没有剩余(只选择一条船）。小饼干算不出来，请你告诉他答案。
输入描述:
输入三个整数a,b,c。（1<=a,b,c<=1000000）
输出描述:
输出一个整数表示答案。
示例1
输入
复制
1 2 3
输出
复制
6
代码：

#include<iostream>
#include<algorithm>

using namespace std;

typedef long long ll;

ll gcb(ll a,ll b)
{
    return b?gcb(b,a%b):a;
}

int main()
{
    ll a,b,c;
    cin>>a>>b>>c;
    ll t=a*b/gcb(a,b);    //a，b的最小公倍数
    ll q=t*c/gcb(t,c);    //a，b的最小公倍数与c的最小公倍数
    cout<<q;

}

(9)聪明的燕姿
城市中人们总是拿着号码牌，不停寻找，不断匹配，可是谁也不知道自己等的那个人是谁。

可是燕姿不一样，燕姿知道自己等的人是谁，因为燕姿数学学得好！

燕姿发现了一个神奇的算法：假设自己的号码牌上写着数字 S，那么自己等的人手上的号码牌数字的所有正约数之和必定等于 S。

所以燕姿总是拿着号码牌在地铁和人海找数字（喂！这样真的靠谱吗）。

可是她忙着唱《绿光》，想拜托你写一个程序能够快速地找到所有自己等的人。

输入格式
输入包含 k 组数据。

对于每组数据，输入包含一个号码牌 S。

输出格式
对于每组数据，输出有两行。

第一行包含一个整数 m，表示有 m 个等的人。

第二行包含相应的 m 个数，表示所有等的人的号码牌。

注意：你输出的号码牌必须按照升序排列。

数据范围
1≤k≤100,
1≤S≤2×109
输入样例：
42
输出样例：
3
20 26 41

代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 50000;

int primes[N], cnt;
bool st[N];

int ans[N], len;

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

bool is_prime(int x)
{
    if (x < N) return !st[x];
    for (int i = 0; primes[i] <= x / primes[i]; i ++ )
        if (x % primes[i] == 0)
            return false;
    return true;
}
// 第一个参数: 上一个用到的质数下标是多少
// 第二个参数：当前这个数是多少
// 第三个参数：当前剩余的s
void dfs(int last, int prod, int s)
{
    if (s == 1)
    {
        ans[len ++ ] = prod;
        return;
    }

    if (s - 1 > (last < 0 ? 1 : primes[last]) && is_prime(s - 1))
        ans[len ++ ] = prod * (s - 1);

    for (int i = last + 1; primes[i] <= s / primes[i]; i ++ )
    {
        int p = primes[i];
        for (int j = 1 + p, t = p; j <= s; t *= p, j += t)
            if (s % j == 0)
                dfs(i, prod * t, s / j);
    }
}

int main()
{
    get_primes(N - 1);

    int s;
    while (cin >> s)
    {
        len = 0;
        dfs(-1, 1, s);

        cout << len << endl;
        if (len)
        {
            sort(ans, ans + len);
            for (int i = 0; i < len; i ++ ) cout << ans[i] << ' ';
            cout << endl;
        }
    }

    return 0;
}