K-D Tree
这东西是我入坑 ICPC 不久就听说过的数据结构,但是一直没去学 QAQ,终于在昨天去学了它。还是挺好理解的,而且也有用武之地。
目录
简介
建树过程
性质
操作
例题
简介
K-D Tree(KDT , k-Dimension Tree) 是一种可以 高效处理 $k$ 维空间信息 的数据结构。更具体地说,它是维护了 $k$ 维空间 $n$ 个点的数据结构,而且它是一棵平衡树。
建树过程
由于二维的形式是竞赛中最常见而且便于讲解,故以二维的情况为例。所以下面构建的都是 2-D Tree。
先使用一个具体的例子来模拟建树的过程:
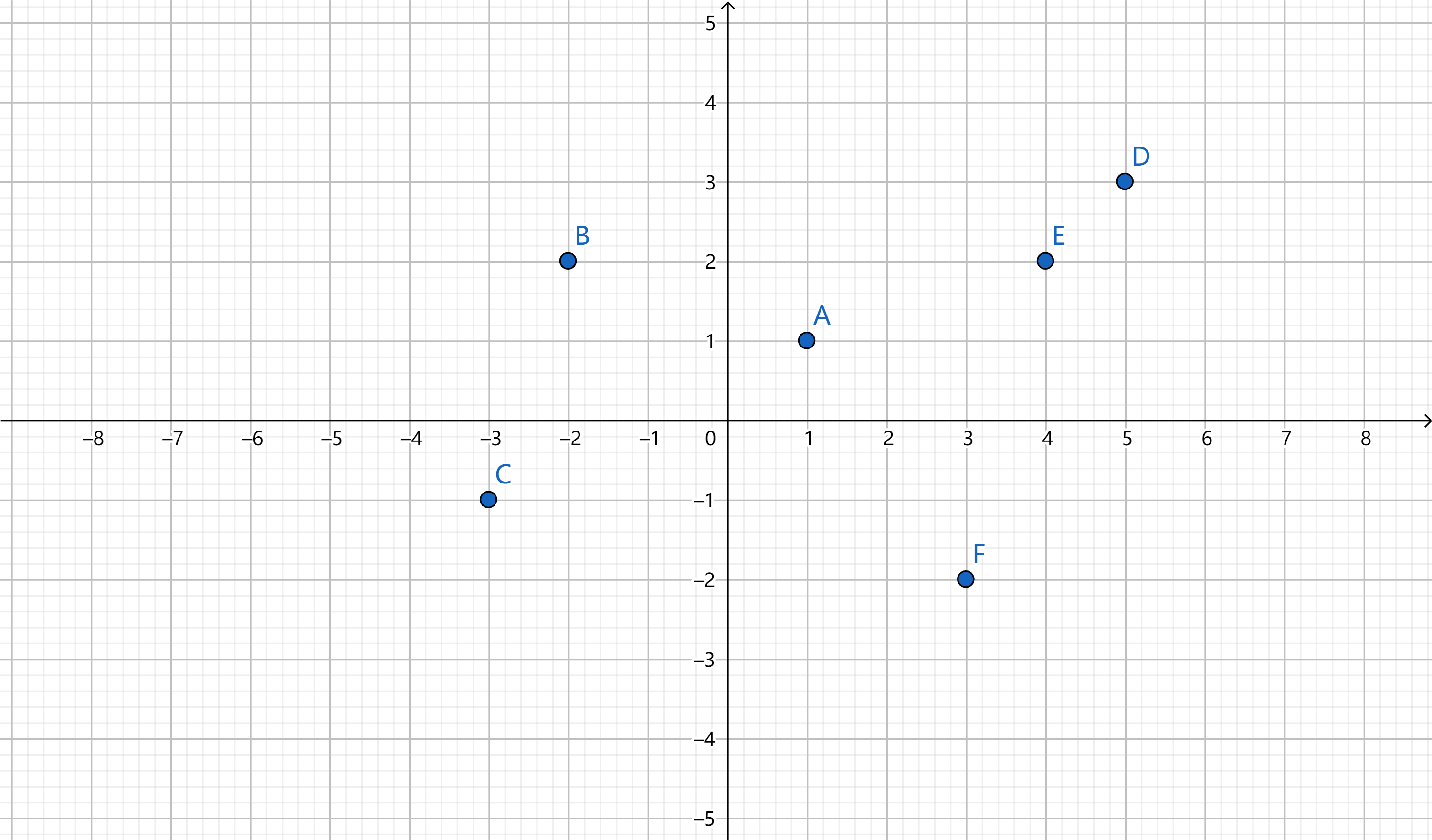
现在如图给出一个点集,接下来开始用这个点集来构建 2-D Tree。
首先,我们以 $x$ 轴坐标(即第一维坐标)为关键字,选取中位数所对应的点为根节点,这里也就是 $A$ 点。
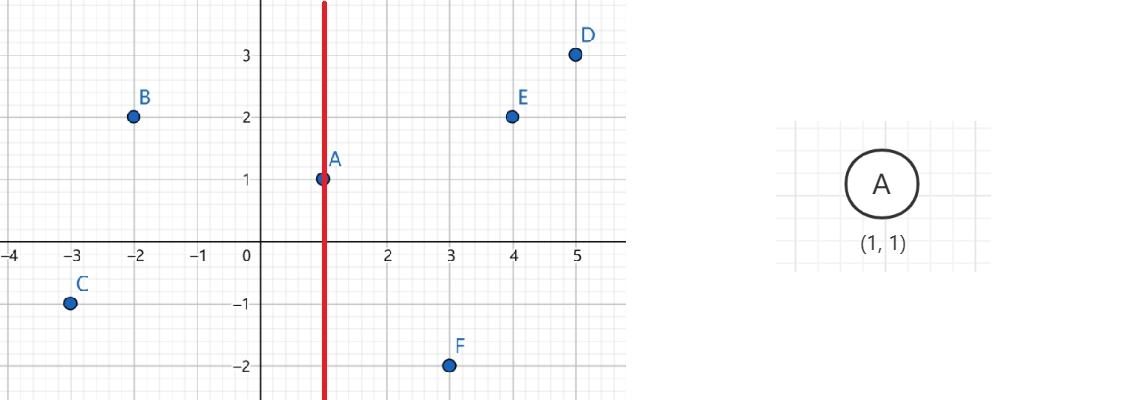
类似地,以 $y$ 轴坐标(即第二维坐标)为关键字,选取中位数所对应的点为根节点,这里也就是 $C$ 和 $E$ 点。
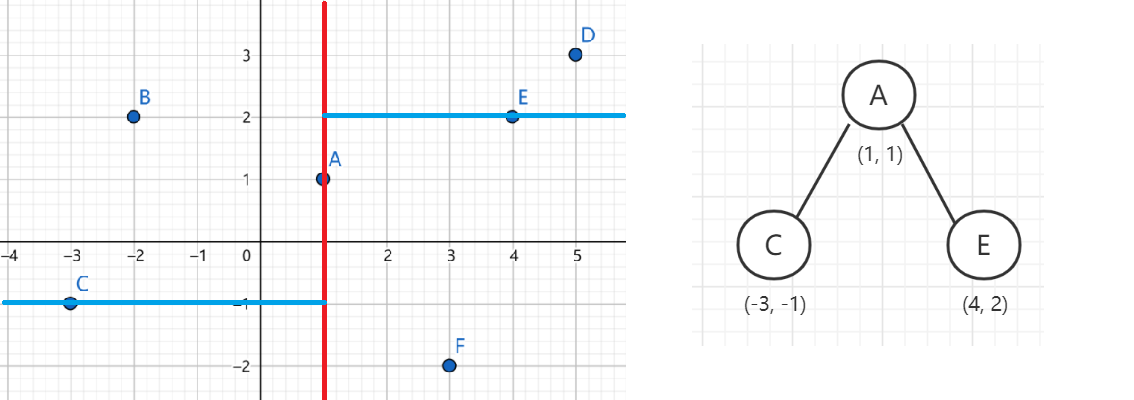
与上面类似,再以 $x$ 轴坐标(即第一维坐标)为关键字继续构建:
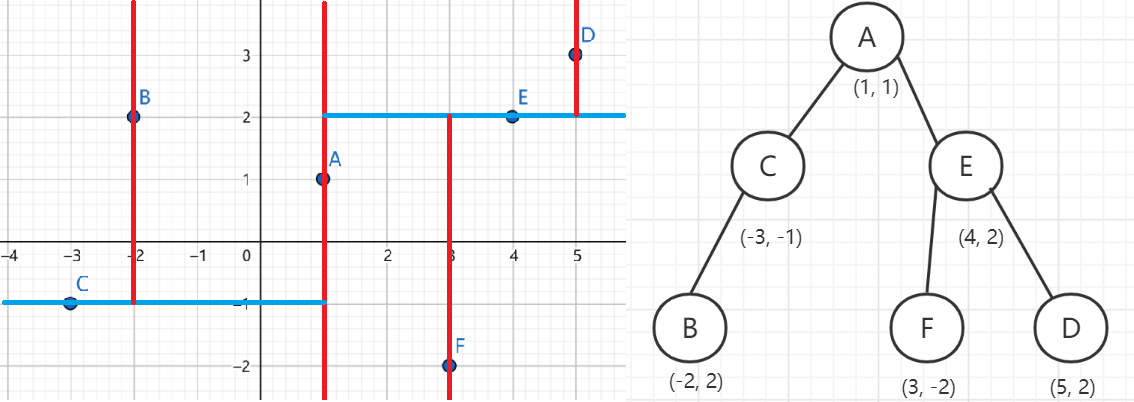
至此,所给出来的点集已经通过一棵二叉树维护了起来。
总结一下建树的过程:
-
以当前的关键字选取中位数所对应的点作为当前子树的根节点。
-
交替地选择不同维度为关键字(如果是 $k$ 维的坐标系那么假设先前选了第 $x$ 维,下一维就是 $x\%k+1$
-
将根节点向左右儿子连边。
性质
- 树的每一层都是按同一个关键字划分。(从上面的建树过程可以明显地看出)
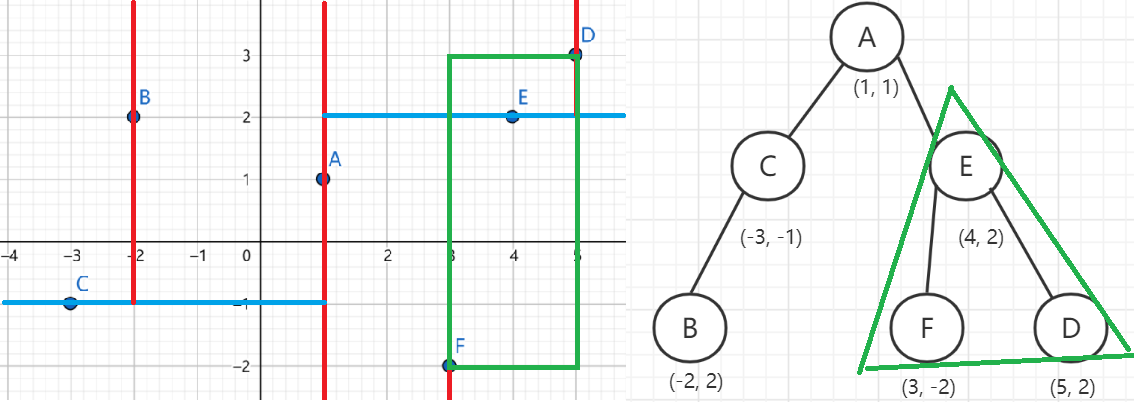
- 树的一棵子树可以划分出一个矩形(二维)。比如下面的 $D,E,F$,只要我们将每个点的坐标维护起来,那么矩形的左下端点就是所有点 $x,y$ 坐标的最小值,右上端点就是所有点 $x,y$ 坐标的最大值。
操作
接下来说一下 K-D Tree 的关键操作。
$\texttt{insert}$
也就是插入操作,和普通的二叉搜索树类似,从根节点开始比较,决定向左子树还是右子树移动,最后走到需要插入的位置。
$\texttt{rebuild}$
即重构操作。
显然,上面的插入操作并不能够保证我们的树高为 $logN$,所以我们需要进行专门的操作来维持树高,换句话说,我们要保证这棵二叉搜索树为平衡树。
怎么保证平衡呢?由上面的性质 $1$ 可知我们不能对树进行旋转,那么可以利用替罪羊树的思想:重构。引入重构常数 $\alpha$,在执行插入操作后,如果发现当前的子树的根节点的左子树或右子树的大小占整棵子树的大小超过 $\alpha$,那么我们就进行重构。
上面说到 K-D Tree 类似于二叉搜索树,因此可以通过它的中序遍历得到一个序列,我们利用这个序列进行重构就可以了。
$\texttt{query}$ 操作因情况而异,故于例题介绍。
例题
例 1:
传送门:
https://www.luogu.com.cn/problem/P4148
分析
操作 $1$ 就是 $\texttt{insert}$,只不过带了点权。
操作 $2$ 是对矩形进行询问,由上面所说的性质 $2$,K-D Tree 的子树正好可以划分出一个矩形,因此我们可以采取类似于线段树区间查询的做法:
- 从根节点出发开始查询。
- 如果当前子树所对应的矩形和查询的矩形没有交集,返回 $0$。
- 如果被当前子树所对应的矩形被查询的矩形包含,直接返回当前子树的权值和 $sum$。
- 否则向左右子树递归继续询问。
代码
#include<bits/stdc++.h>
using namespace std;
#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
inline void read(int &x){
int s=0; x=1;
char ch=getchar();
while(ch<'0' || ch>'9') {if(ch=='-')x=-1;ch=getchar();}
while(ch>='0' && ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
x*=s;
}
const int N=5e5+5;
struct Point{
int x[2], w;
};
struct Node{
int l, r;
Point P;
int L[2], R[2], sum, sz;
#define ls tr[u].l
#define rs tr[u].r
}tr[N];
int n;
int idx, root;
int buf[N], tot;
int add(){
if(!tot) return ++idx;
return buf[tot--];
}
void pushup(int u){
auto &L=tr[ls], &R=tr[rs];
tr[u].sum=tr[u].P.w+L.sum+R.sum, tr[u].sz=L.sz+R.sz+1;
rep(i,0,1){
tr[u].L[i]=min(tr[u].P.x[i], min(L.L[i], R.L[i]));
tr[u].R[i]=max(tr[u].P.x[i], max(L.R[i], R.R[i]));
}
}
const double Al=0.72;
Point pt[N];
void getSeq(int u, int cnt){
if(ls) getSeq(ls, cnt);
buf[++tot]=u, pt[tr[ls].sz+1+cnt]=tr[u].P;
if(rs) getSeq(rs, cnt+tr[ls].sz+1);
}
int rebuild(int l, int r, int k){
if(l>r) return 0;
int mid=l+r>>1;
int u=add();
nth_element(pt+l, pt+mid, pt+r+1, [&](Point a, Point b){
return a.x[k]<b.x[k];
});
tr[u].P=pt[mid];
ls=rebuild(l, mid-1, k^1), rs=rebuild(mid+1, r, k^1);
pushup(u);
return u;
}
void maintain(int &u, int k){
if(tr[u].sz*Al<tr[ls].sz || tr[u].sz*Al<tr[rs].sz)
getSeq(u, 0), u=rebuild(1, tot, k);
}
void insert(int &u, Point p, int k){
if(!u){
u=add();
tr[u].l=tr[u].r=0;
tr[u].P=p, pushup(u);
return;
}
if(p.x[k]<=tr[u].P.x[k]) insert(ls, p, k^1);
else insert(rs, p, k^1);
pushup(u);
maintain(u, k);
}
bool In(Node t, int x1, int y1, int x2, int y2){
return t.L[0]>=x1 && t.R[0]<=x2 && t.L[1]>=y1 && t.R[1]<=y2;
}
bool In(Point p, int x1, int y1, int x2, int y2){
return p.x[0]>=x1 && p.x[0]<=x2 && p.x[1]>=y1 && p.x[1]<=y2;
}
bool Out(Node t, int x1, int y1, int x2, int y2){
return t.R[0]<x1 || t.L[0]>x2 || t.R[1]<y1 || t.L[1]>y2;
}
int query(int u, int x1, int y1, int x2, int y2){
if(In(tr[u], x1, y1, x2, y2)) return tr[u].sum;
if(Out(tr[u], x1, y1, x2, y2)) return 0;
int res=0;
if(In(tr[u].P, x1, y1, x2, y2)) res+=tr[u].P.w;
res+=query(ls, x1, y1, x2, y2)+query(rs, x1, y1, x2, y2);
return res;
}
int main(){
cin>>n;
// init
tr[0].L[0]=tr[0].L[1]=N+5;
tr[0].R[0]=tr[0].R[1]=-1;
int res=0, op;
while(cin>>op, op!=3){
if(op==1){
int x, y, k; read(x), read(y), read(k);
insert(root, {x^res, y^res, k^res}, 0);
}
else{
int x1, y1, x2, y2; read(x1), read(y1), read(x2), read(y2);
cout<<(res=query(root, x1^res, y1^res, x2^res, y2^res))<<endl;
}
}
return 0;
}
例 2:
传送门:
https://www.acwing.com/problem/content/256/
https://www.luogu.com.cn/problem/P4169
(注意两个 OJ 的数据有差异)
分析
操作 $1$ 就是 $\texttt{insert}$。
操作 $2$ 我们采取搜索剪枝的方法:
- 从根节点出发询问,记现在查询到 $u$ 点了。
- 用 $u$ 点和查询点的距离更新答案。
- 求查询点与 $u$ 点的左右子树(分别对应两个矩形)的期望距离(我将其称为估价函数),也就是这个点到矩形的最小曼哈顿距离。并决定是否向该子树递归。
因为用到这样的搜索了,复杂度是 $O(能过)$,但是实际运行效果非常不错,我的代码在洛谷可以到最优解的第二页,而且最优解的前几名大多是用 K-D Tree 写的;同时,在 acwing 的运行时是 $5628 ms$,而选取几份使用 $cdq$ 分治的却都在 $10000 ms$ 左右。
// Problem: 天使玩偶
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/description/256/
// Memory Limit: 256 MB
// Time Limit: 7000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#include<bits/stdc++.h>
using namespace std;
namespace IO{
int f; char c;
template<typename T> inline void read(T &v){
v = 0; f = 1; c = getchar();
while(!isdigit(c)) { if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)) { v = (v << 3) + (v << 1) + (int)(c - '0'); c = getchar(); }
v *= f;
return;
}
template<typename T> inline void write(T k){
if(k < 0) { putchar('-'); k = -k; }
if(k > 9) write(k / 10);
putchar((char)(k % 10 + '0'));
return;
}
inline int Read() { int v; read(v); return v; }
inline void Write(int v, char ed = '\n') { write(v); putchar(ed); return; }
}
#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
using IO::read;
using IO::Write;
const int N=1e6+5, INF=0x3f3f3f3f;
struct Point{
int x[2];
};
struct Node{
int l, r;
Point P;
int L[2], R[2], sz;
#define ls tr[u].l
#define rs tr[u].r
}tr[N];
int n, m;
int idx, root;
int buf[N], tot;
int add(){
if(!tot) return ++idx;
return buf[tot--];
}
void pushup(int u){
auto &L=tr[ls], &R=tr[rs];
tr[u].sz=L.sz+R.sz+1;
rep(i,0,1){
tr[u].L[i]=min(tr[u].P.x[i], min(L.L[i], R.L[i]));
tr[u].R[i]=max(tr[u].P.x[i], max(L.R[i], R.R[i]));
}
}
const double Al=0.75;
Point pt[N];
void getSeq(int u, int cnt){
if(ls) getSeq(ls, cnt);
buf[++tot]=u, pt[tr[ls].sz+1+cnt]=tr[u].P;
if(rs) getSeq(rs, cnt+tr[ls].sz+1);
}
int rebuild(int l, int r, int k){
if(l>r) return 0;
int mid=l+r>>1;
int u=add();
nth_element(pt+l, pt+mid, pt+r+1, [&](Point a, Point b){
return a.x[k]<b.x[k];
});
tr[u].P=pt[mid];
ls=rebuild(l, mid-1, k^1), rs=rebuild(mid+1, r, k^1);
pushup(u);
return u;
}
void maintain(int &u, int k){
if(tr[u].sz*Al<tr[ls].sz || tr[u].sz*Al<tr[rs].sz)
getSeq(u, 0), u=rebuild(1, tot, k);
}
void insert(int &u, Point p, int k){
if(!u){
u=add();
tr[u].l=tr[u].r=0;
tr[u].P=p, pushup(u);
return;
}
if(p.x[k]<=tr[u].P.x[k]) insert(ls, p, k^1);
else insert(rs, p, k^1);
pushup(u);
maintain(u, k);
}
int dis(Point a, Point b){
return abs(a.x[0]-b.x[0])+abs(a.x[1]-b.x[1]);
}
int H(Node t, Point p){
int x=p.x[0], y=p.x[1];
return max(0, t.L[0]-x)+max(0, t.L[1]-y)+max(0, x-t.R[0])+max(0, y-t.R[1]);
}
int res;
void query(int u, Point p){
if(!u) return;
res=min(res, dis(tr[u].P, p));
int LV=INF, RV=INF;
if(ls) LV=H(tr[ls], p);
if(rs) RV=H(tr[rs], p);
if(LV<RV){
if(LV<res) query(ls, p);
if(RV<res) query(rs, p);
}
else{
if(RV<res) query(rs, p);
if(LV<res) query(ls, p);
}
}
int main(){
cin>>n>>m;
// init
tr[0].L[0]=tr[0].L[1]=N+5;
tr[0].R[0]=tr[0].R[1]=-1;
rep(i,1,n){
int x, y; read(x), read(y);
pt[i]={x, y};
}
root=rebuild(1, n, 0);
rep(i,1,m){
int op, x, y; read(op), read(x), read(y);
if(op==1) insert(root, {x, y}, 0);
else{
res=INF;
query(root, {x, y});
Write(res);
}
}
return 0;
}


佬想问下单次查询的时间复杂度和维持平衡的时间复杂度
指第一题
查询复杂度是 $O(\sqrt N)$,维持平衡可以发现其实本质就是替罪羊树的操作,均摊 $O(logN)$