（1）递归实现排列型枚举
把 1∼n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式
一个整数 n。

输出格式
按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围
1≤n≤9
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

const int N =10;
bool st[N];
int path[N];
int n;
int m;

void dfs(int u)
{
      if (u > n)  // 边界
    {
        m--;
        if(m==0)
        {
            for (int i = 1; i <= n; i ++ ) printf("%d ", path[i]); // 打印方案
        }
        puts("");
        return;
    }
    for(int i=1;i<=n;i++)
    {
        if(!st[i])
        {
            path[u]=i;
            st[i]=true;
            dfs(u+1);

            path[u]=0;
            st[i]=false;
        }
    }
}


int main()
{
    scanf("%d%d",&n,&m);
    dfs(1);
    return 0;
}

(1.1)递归实现排列类型枚举 II
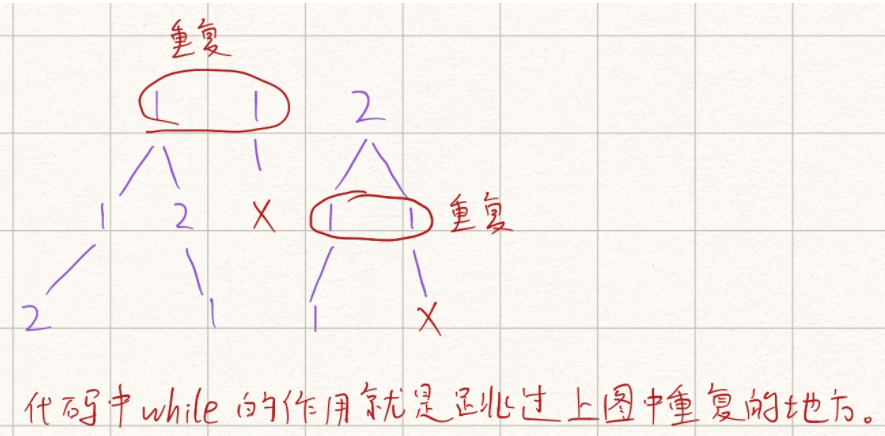
给定一个长度为 n 的可包含重复数字的序列，请你求出其所有不重复的全排列。

输入格式
第一行包含整数 n。

第二行包含 n 个整数。

输出格式
输出所有的不同排列，每种排列占一行。

在确定每种排列的输出顺序时，第一个数较小的先输出，第一个数相同时，第二个数较小的先输出，以此类推。

数据范围
1≤n≤9,
数组中包含的元素的取值范围 [1,9]
输入样例：
3
1 1 2
输出样例：
1 1 2
1 2 1
2 1 1
难度：简单
时/空限制：1s / 64MB
总通过数：836
总尝试数：1786
来源：AcWing
算法标签

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 11;
int a[N];
int nums[N];
bool st[N];
int n;

void dfs(int u)
{
    if(u==n)
    {
        for(int i=0;i<n;i++)cout<<nums[i]<<" ";
        cout<<endl;
        return ;
    }

    for(int i=0;i<n;i++)
    {
        if(!st[i])
        {
            st[i]=true;
            nums[u]=a[i];
            dfs(u+1);
            st[i]=false;
            while(i+1<n&&a[i+1]==a[i])i++; //同一层
        }

    }
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)cin>>a[i];

    sort(a,a+n);

    dfs(0);

}

(2)递归实现指数型枚举
从 1∼n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式
输入一个整数 n。

输出格式
每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 1 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围
1≤n≤15
输入样例：
3
输出样例：

3
2
2 3
1
1 3
1 2
1 2 3
代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>

using namespace std;

const int N =16;
int n;
int f[N];
vector<vector<int>> ways;
void dfs(int u)
{
    if(u>n)
    {
        vector<int> way;
        for(int i=1;i<=n;i++)
        {
            if(f[i]==1)
            {
                way.push_back(i);
            }
        }
        ways.push_back(way);
        return;
    }
    f[u]=2;
    dfs(u+1);
    f[u]=0;

    f[u]=1;
    dfs(u+1);
    f[u]=0;
}

int main()
{
    scanf("%d",&n);
    dfs(1);
    for(int i=0;i<ways.size();i++)
    {
        for(int j=0;j<ways[i].size();j++)
        {
            printf("%d ",ways[i][j]);
        }
        printf("\n");
    }
    return 0;
}

（3）递归实现组合型枚举

从 1∼n 这 n 个整数中随机选出 m 个，输出所有可能的选择方案。

输入格式
两个整数 n,m ,在同一行用空格隔开。

输出格式
按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

数据范围
n>0 ,
0≤m≤n ,
n+(n−m)≤25
输入样例：
5 3
输出样例：
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
思考题：如果要求使用非递归方法，该怎么做呢？

难度：简单
时/空限制：5s / 256MB
总通过数：17859
总尝试数：25521
来源：《算法竞赛进阶指南》
算法标签
代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 30;

int n, m;
int way[N];

void dfs(int u, int start)
{
    if (u + n - start < m) return;  // 剪枝 剩下的数不足m个，直接剪掉 已经选了u-1个 还可以选n-start+1个
    if (u > m)
    {
        for (int i = 1; i <= m; i ++ ) printf("%d ", way[i]);
        puts("");
        return;
    }

    for (int i = start; i <= n; i ++ )
    {
        way[u] = i;
        dfs(u + 1, i + 1);
        way[u] = 0; // 恢复现场,可要可不要
    }
}

int main()
{
    scanf("%d%d", &n, &m);

    dfs(1, 1);

    return 0;
}

（4）n-皇后问题
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

1_597ec77c49-8-queens.png

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式
共一行，包含整数 n。

输出格式
每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围
1≤n≤9
输入样例：
4
输出样例：
.Q..
…Q
Q…
..Q.

..Q.
Q…
…Q
.Q..

代码：

#include <iostream>
using namespace std;
const int N = 20; 

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u) {
    // u == n 表示已经搜了n行，故输出这条路径
    if (u == n) {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   // 等价于cout << g[i] << endl;
        puts("");  // 换行
        return;
    }

    //对n个位置按行搜索
    for (int i = 0; i < n; i ++ )
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        // udg[n - u + i]，+n是为了保证下标非负
        if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
            g[u][i] = '.';

        }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}   

总结：对角线 dg[u+i]dg[u+i]，反对角线udg[n−u+i]udg[n−u+i]中的下标 u+iu+i和 n−u+in−u+i 表示的是截距

下面分析中的(x,y)(x,y)相当于上面的(u,i)

代码：

// 不同搜索顺序 时间复杂度不同  所以搜索顺序很重要！
#include <iostream>
using namespace std;
const int N = 20;

int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索，所以加了row

// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
    // 处理超出边界的情况
    if (y == n) y = 0, x ++ ;

    if (x == n) { // x==n说明已经枚举完n^2个位置了
        if (s == n) { // s==n说明成功放上去了n个皇后
            for (int i = 0; i < n; i ++ ) puts(g[i]);
            puts("");
        }
        return;
    }

    // 分支1：放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
        g[x][y] = '.';
    }

    // 分支2：不放皇后
    dfs(x, y + 1, s);
}


int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0, 0, 0);

    return 0;
}