算法思想
$A^*$算法在应用上与双向广搜相同 — 优化状态相对较多的最小步数模型.
大致思路: 通过启发函数, 尽量只走最有可能是最短路的路径 — 通过预测每个点到终点路径的距离,
每次走预测路径最短的顶点. 这样做的好处是我们只走了距离较短的路径, 以减少遍历状态的数目.
算法流程
-
优先队列替换$bfs$的普通队列, 保存键值对
<顶点$v$, $(d(v) + f(v))$>.
其中$d(v)$: 起点到顶点$v$路径的距离(不一定是最短路径); $f(v)$: 顶点$v$到终点的估计距离.
优先队列每次取$d(v) + f(v)$最小的顶点出队. -
$v$出队后更新相邻顶点的$d$值, 更新与入队操作类似$dijkstra$算法.
-
终点出队, 算法结束.
正确性证明
前提条件
设对于顶点$u$:
-
$d(u)$: 当前路径起点到$u$的距离.
-
$g(u)$: 顶点$u$到终点的最短距离.
-
$f(u)$: 顶点$u$到终点的预测距离, 也就是之前提到的启发函数.
算法正确性前提: $0\le f(u)\le g(u)$. (在此基础上$f(u)$越接近$g(u)$越好).
证明: (反证法)
终点出队时算法结束, 找到起点到终点的最短路. 假设终点出队时, 对应距离不是最短距离.
由于出队时不是最短距离, $d_{出队}\gt d_{最优}$.
对于最短路径上的某点$u$:
$\;\;\;\;\;\;d(u) + f(u)\le d(u) + g(u) = d_{最优}\lt d_{出队}$.
而优先队列按$d + f$的最小值出队, 即$d_{出队}\le d_{最优}$.
二者矛盾.
应用条件
-
图中无负环即可. 不同于$bfs$, $A^*$可应用在权重为任意值的图上.
-
存在最短路, 即问题有解. 否则算法最终会遍历所有状态(预测值都为$+\infty$), 并且
优先队列每次操作的时间复杂度为$O(\lg(n))$, 此时$A^*$甚至比普通$bfs$时间性能还要差.
$A^\*$算法与$dijkstra$算法过程类似, $dijkstra$算法类似于所有顶点启发函数为0的$A^*$算法.
不过$A^*$算法应用场景的顶点数较多, 且只关注起点到终点的最短距离,
而$dijktra$算法考虑起点到其他任意顶点的最短路径.
简单比较几个算法的最小值确定时间:
-
$bfs$: 入队时确定顶点最小距离.
-
$dijkstra$: 出队时确定顶点最小距离.
-
$A^*$: 出队时确定终点的最小距离, 其他顶点无法保证.
最短距离的确定
$A^*$算法只能保证终点出队时最短, 其他顶点无法保证(预测终究是预测), 下面举一个实例.
假设图中边权均为1, 除起点$s$和终点$e$外, 其他顶点已表明其启发函数值:
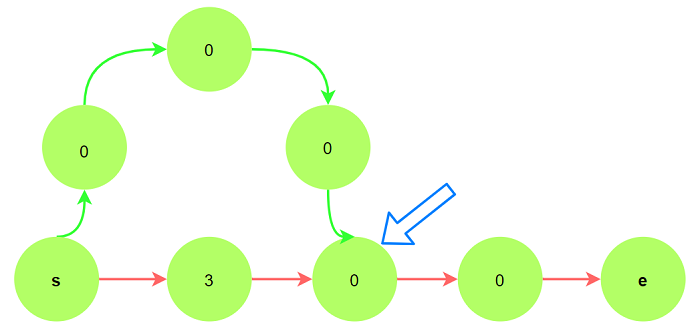
可以观察到红色路径为起点$s$到终点$e$的最短路径, 然而由于红色路径第一个顶点的启发函数值为3,
其权重为4, 按照算法步骤, 首先会将绿色路径上顶点入队 --> 出队, 直到箭头指向顶点出队, 其
出队时距离为$4$, 并非实际最小距离$3$.
那么为何算法可能首先入队出队的并非最短路径, 最后还是会找到最短路径而不是提前出队终点呢?
这是因为启发函数$f\ge 0$, 而随着顶点接近终点, 其权重中起点到顶点的真实距离占比越来越大.
对于非最短路径上的顶点到达终点的路径距离$d\gt d_{最优}$, 而最短路径上顶点的权值$d + f\le d_{最优}$,
所以算法最终还是会选择最短路径上的顶点更新后续顶点.

