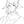图的储存主要有两种方式：
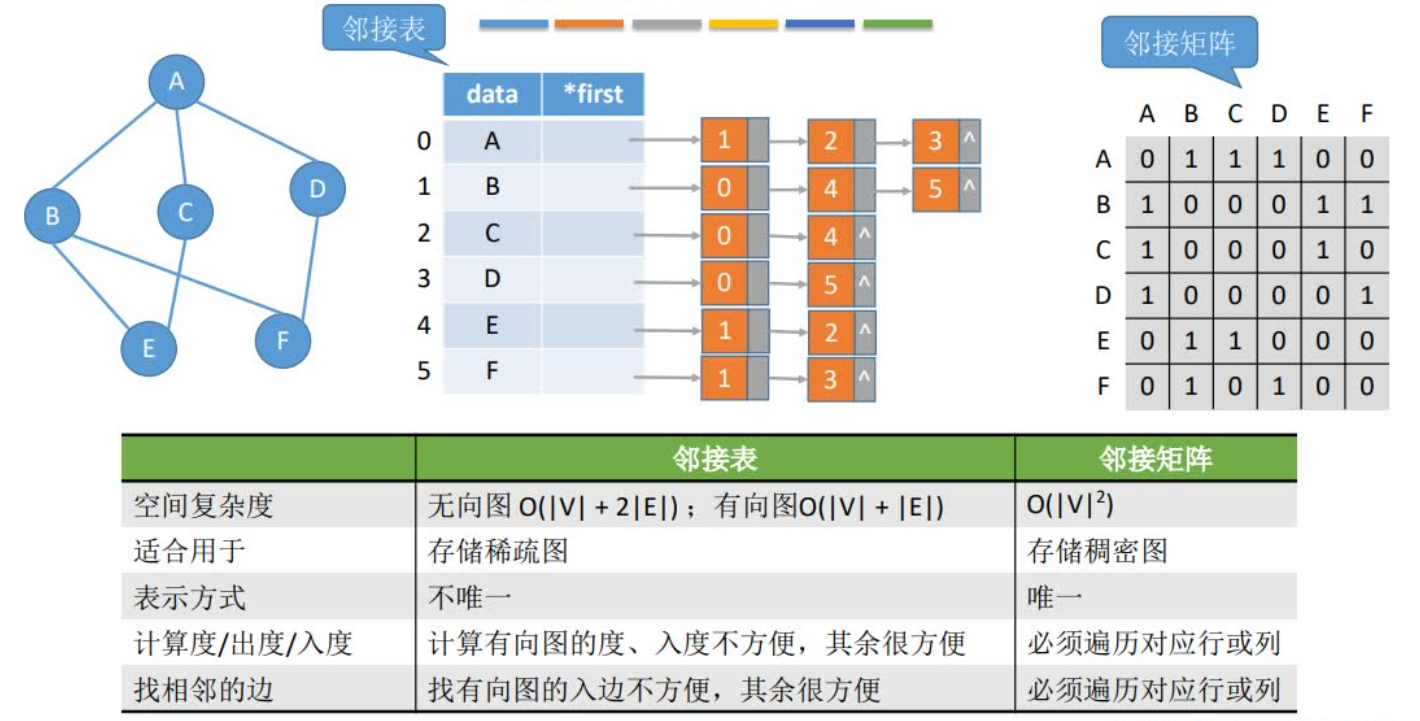
1.邻接矩阵
2.邻接表
其他的常用的还有十字链表，临界多重表
邻接矩阵
邻接矩阵的好处：
邻接矩阵是以数组的形式实现图的储存的
（1）直观、简单、好理解
（2）方便检查任意一对定点间是否存在边
（3）方便找任一顶点的所有“邻接点”（有边直接相连的顶点）
（4）方便计算任一顶点的度
邻接矩阵的局限性：时间复杂度O(n^2），空间复杂度O(n^2)
（1）浪费空间。对于稠密图还是很合算的，但是对于稀疏图（点很多而边很少）有大量无效元素。
（2）浪费时间。要确定图中有多少条边，则必须按行、按列对每个元素进行检测，所花费的时间代价很大。

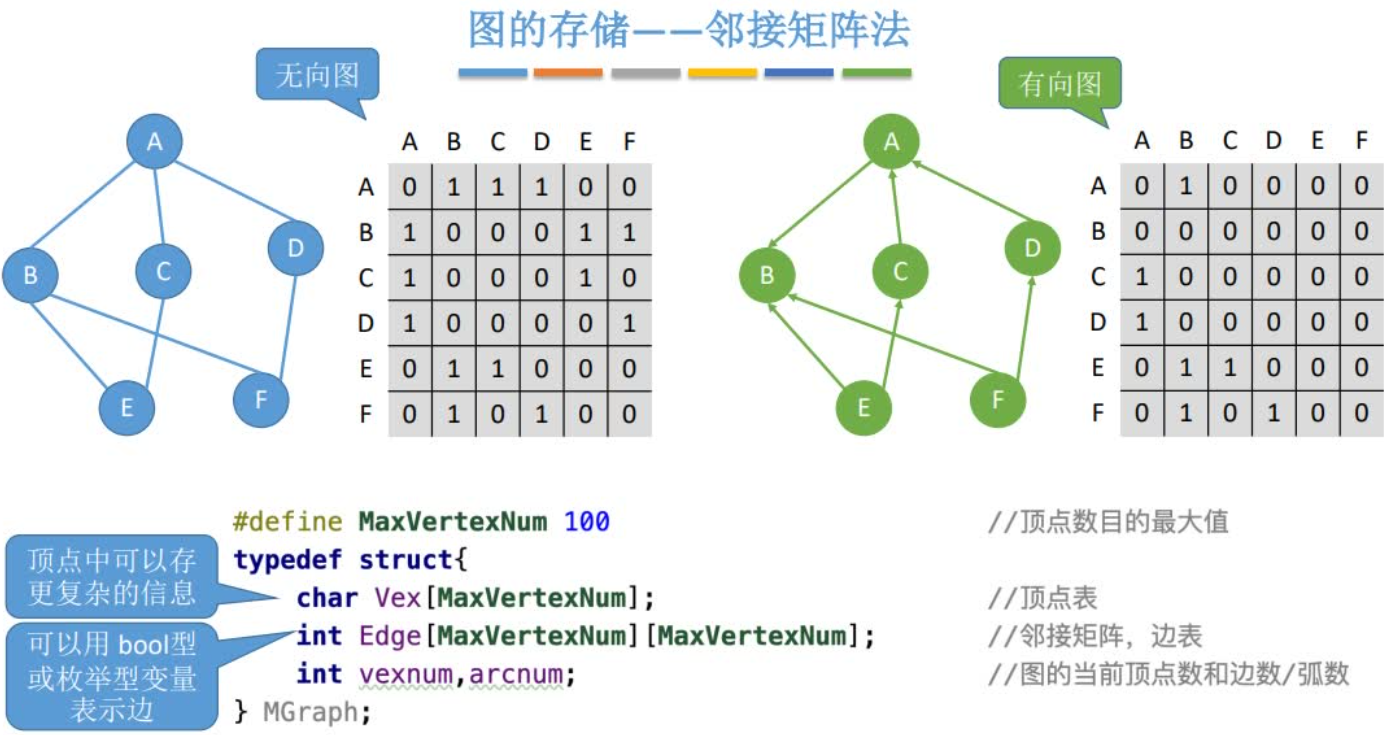
结点数为n的图G= (V,E)的邻接矩阵A是n´n的。将G的顶点编号为v1,v2,…,vn，则

第i个结点的度=第i行（或第i列）的非零元素个数
第i个结点的出度=第i行的非零元素个数
第i个结点的入度=第i列的非零元素个数
第i个结点的度=第i行、第i列的非零元素个数之和
邻接矩阵法求顶点的度/出度/入度的时间复杂度为O(|V|)

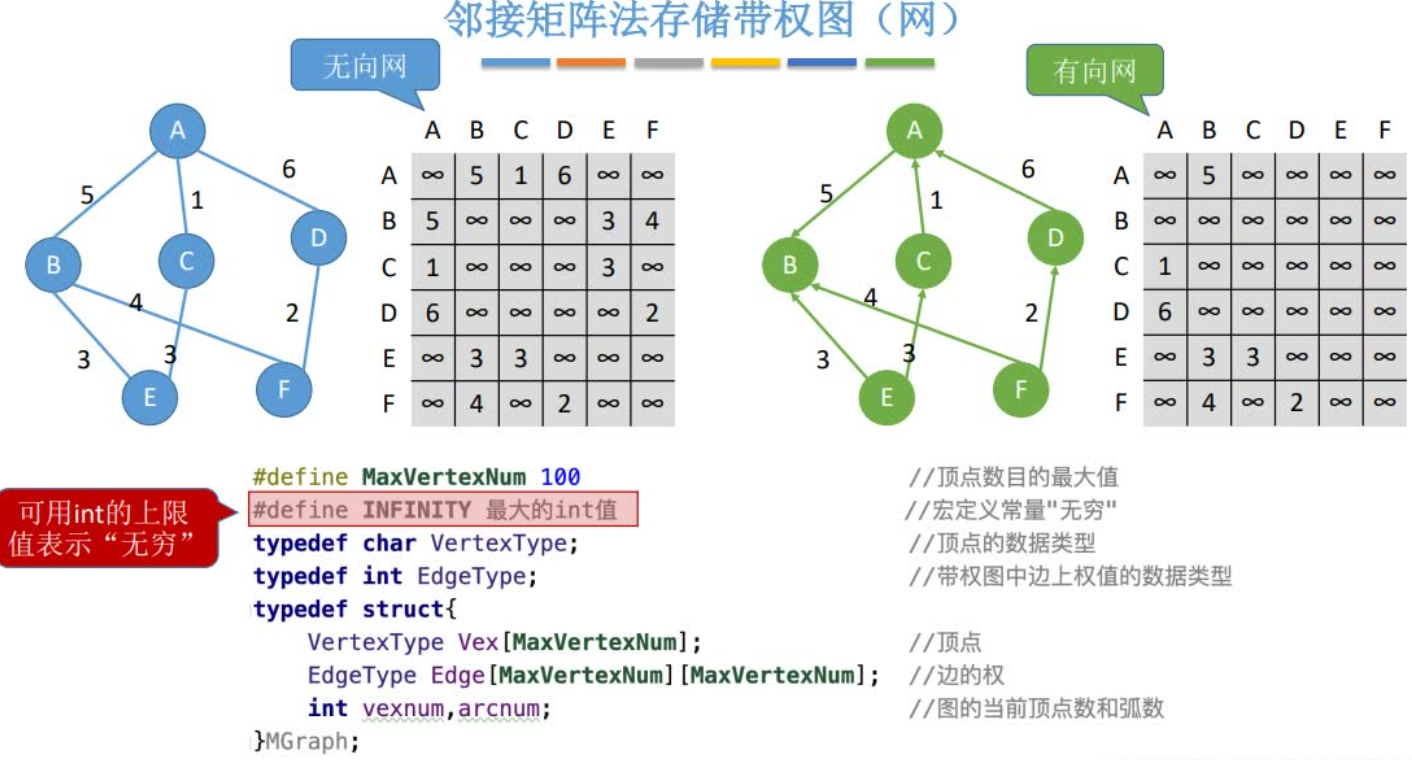
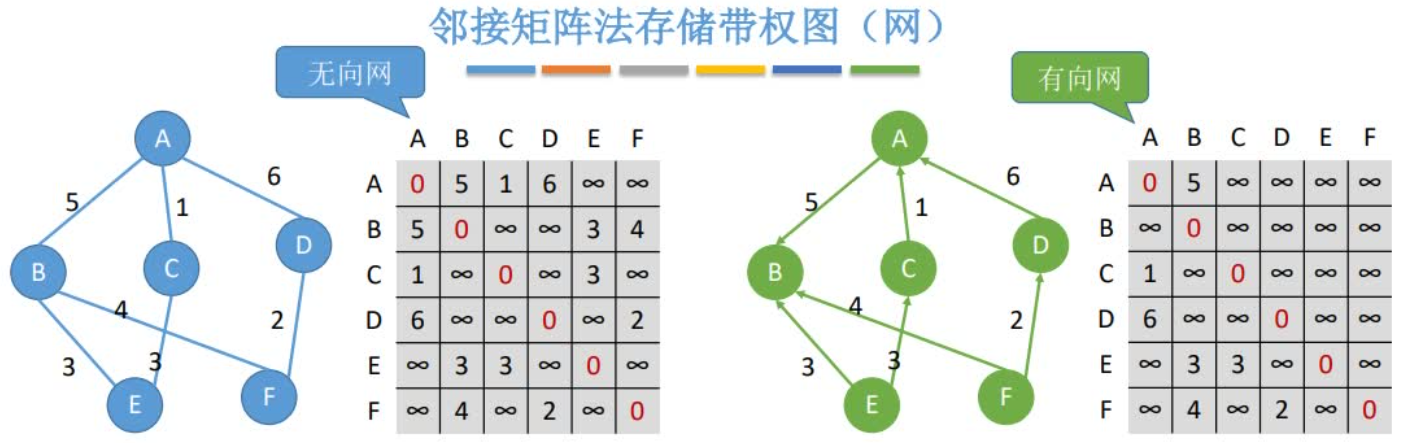
空间复杂度：O(|V|2)——只和顶点数相关，和实际的边数无关适合用于存储稠密图
无向图的邻接矩阵是对称矩阵，可以压缩存储（只存储上三角区/下三角区）


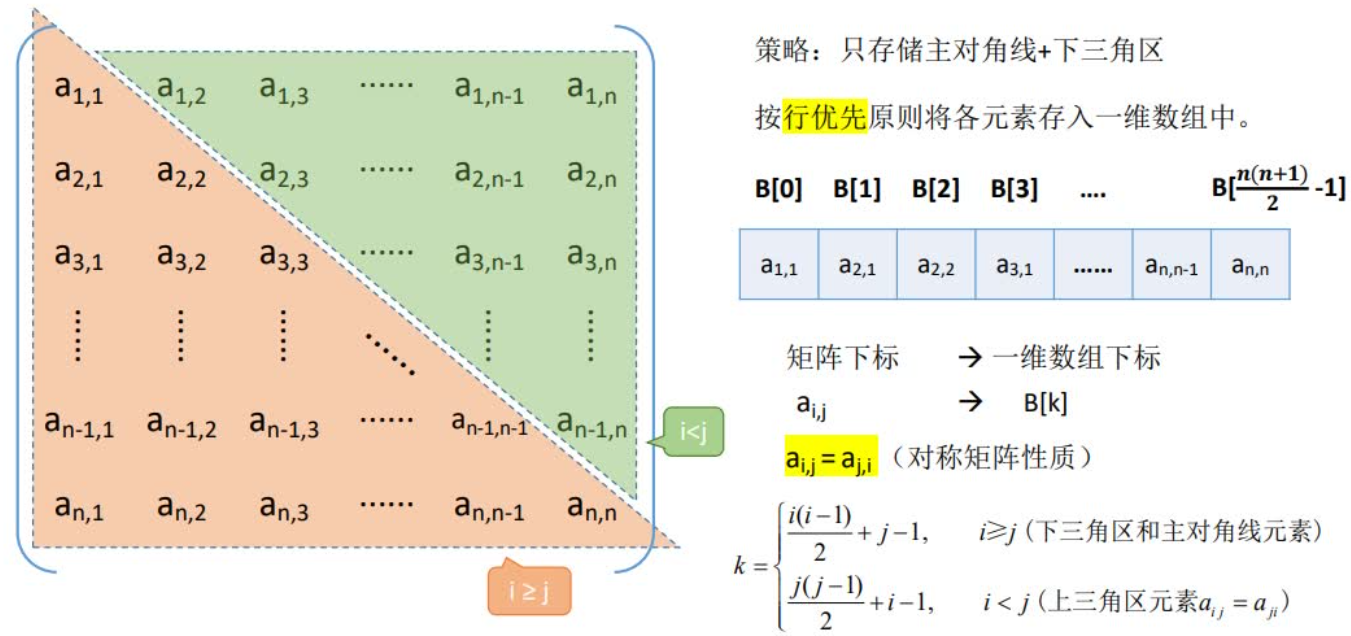
性质

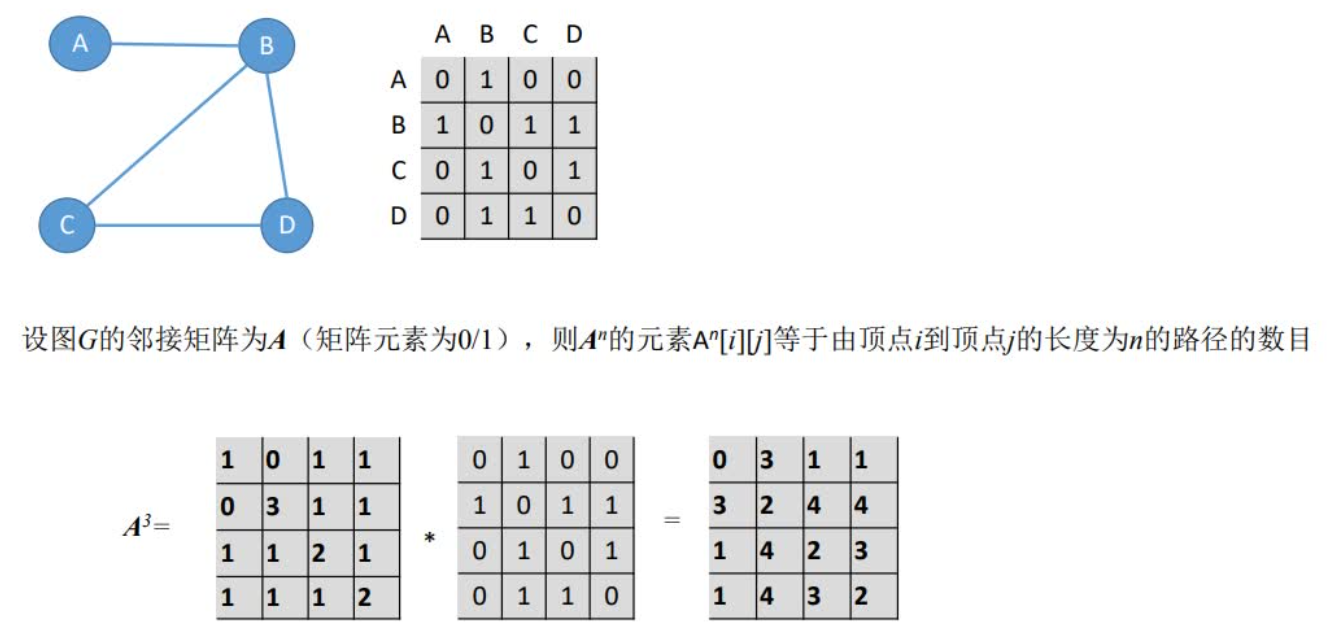
邻接表

图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法

在邻接表中，对图中每个顶点建立一个单链表，第i个单链表中的节点表示依附于顶点i的边（对有向图是以顶点i为尾的边）。每个单链表上附设一个表头节点。


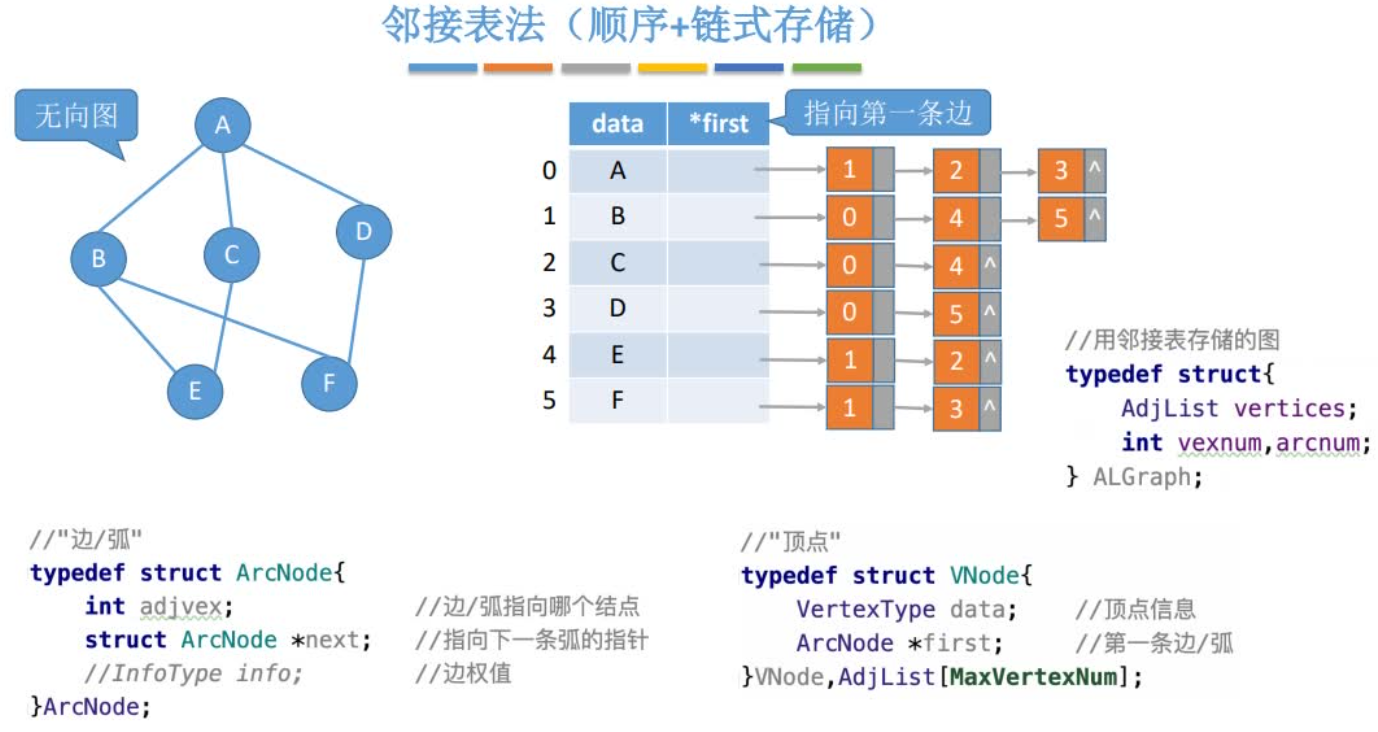
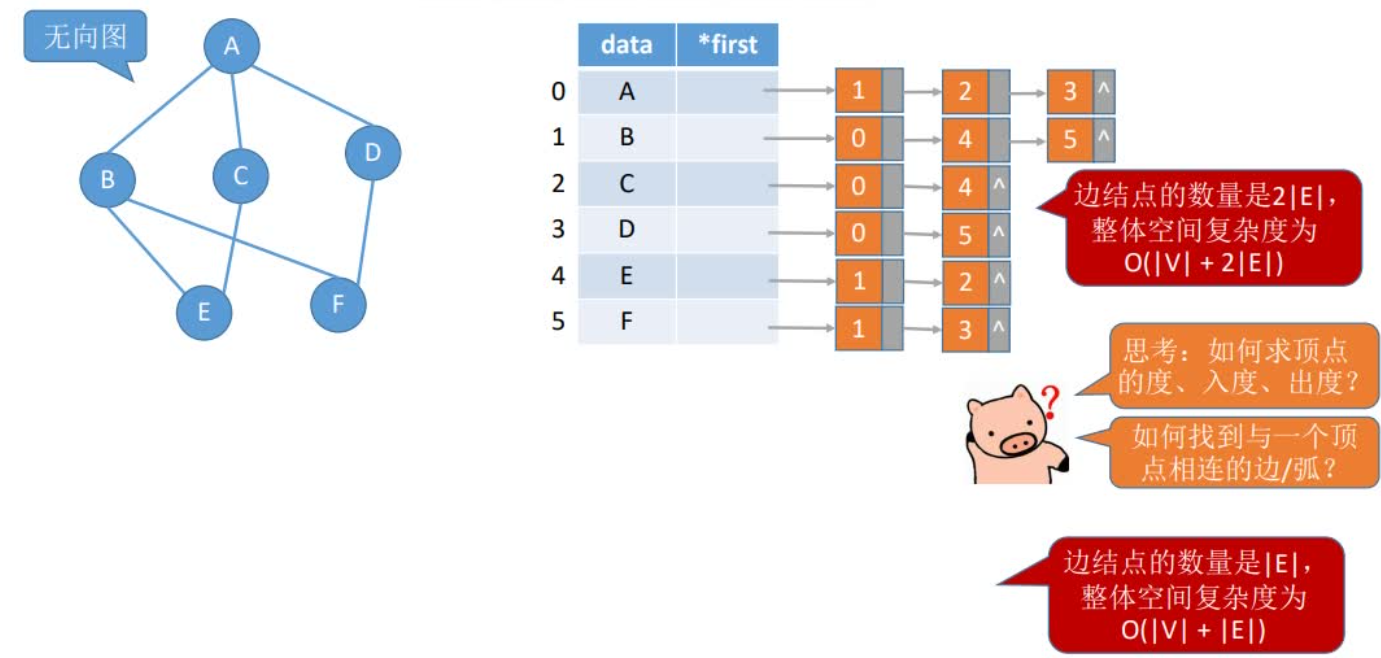
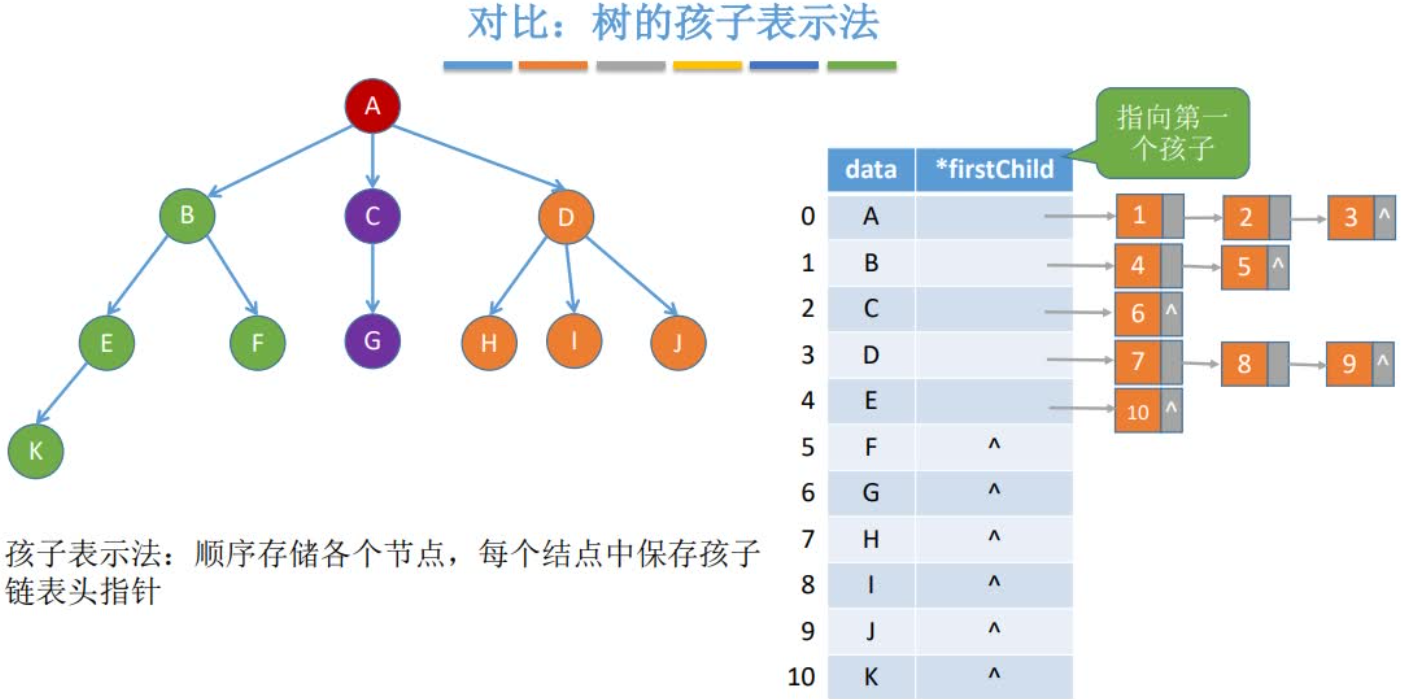
对比：树的孩子表示法


邻接表的特点

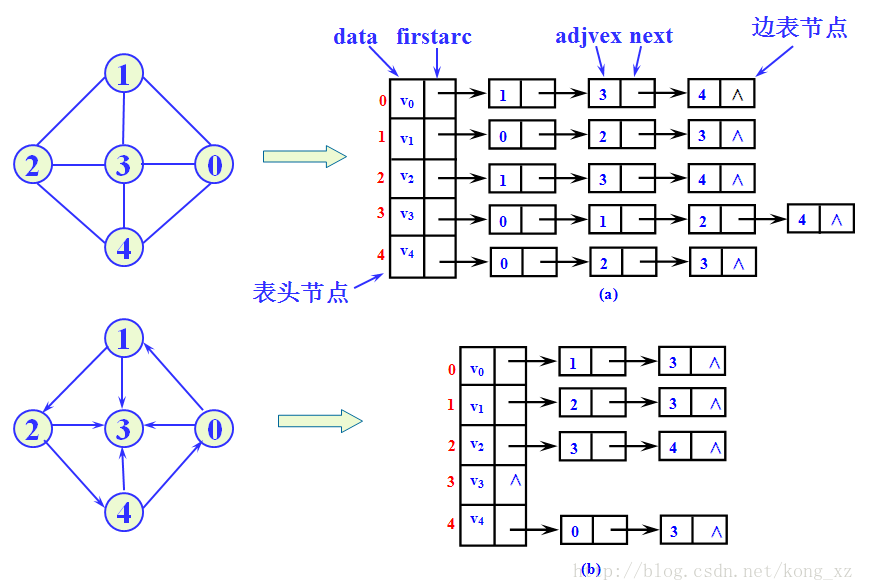
（1）邻接表表示不唯一。这是因为在每个顶点对应的单链表中，各边节点的链接次序可以是任意的，取决于建立邻接表的算法以及边的输入次序。
（2）对于有n个顶点和e条边的无向图，其邻接表有n个顶点节点和2e个边节点。显然，在总的边数小于n(n-1)/2的情况下，邻接表比邻接矩阵要节省空间。
（3）对于无向图，邻接表的顶点i对应的第i个链表的边节点数目正好是顶点i的度。
（4）对于有向图，邻接表的顶点i对应的第i个链表的边节点数目仅仅是顶点i的出度。其入度为邻接表中所有adjvex域值为i的边节点数目。