(1) Floyd求最短路
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
接下来 k 行,每行包含两个整数 x,y,表示询问点 x 到点 y 的最短距离。
输出格式
共 k 行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出 impossible。
数据范围
1≤n≤200,
1≤k≤n2
1≤m≤20000,
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出样例:
impossible
1
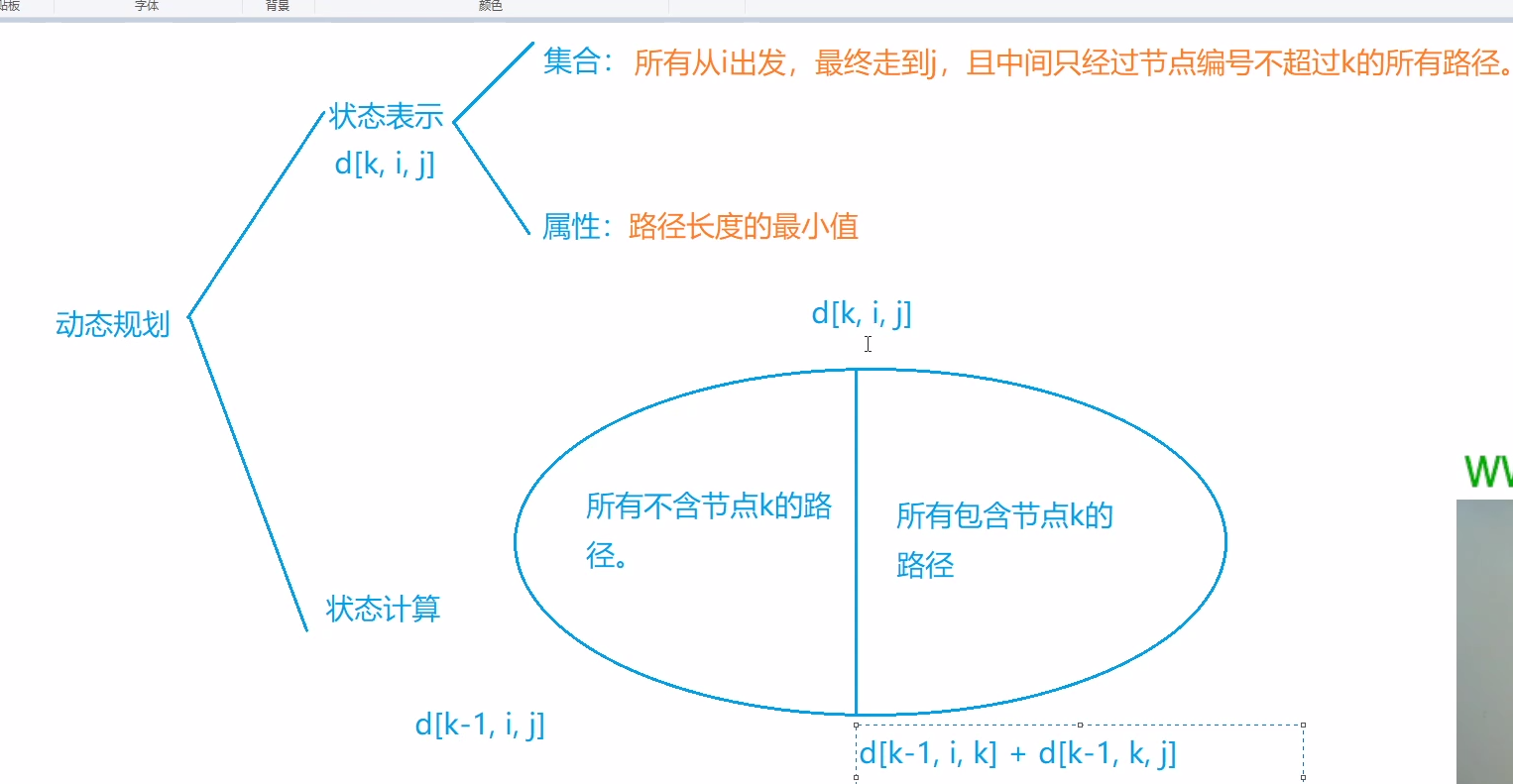
f[i, j, k]表示从i走到j的路径上除i和j点外只经过1到k的点的所有路径的最短距离。那么f[i, j, k] = min(f[i, j, k - 1), f[i, k, k - 1] + f[k, j, k - 1]。
因此在计算第k层的f[i, j]的时候必须先将第k - 1层的所有状态计算出来,所以需要把k放在最外层。
代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 210, INF = 1e9;
int n, m, Q;
int d[N][N];
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main()
{
scanf("%d%d%d", &n, &m, &Q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = min(d[a][b], c);
}
floyd();
while (Q -- )
{
int a, b;
scanf("%d%d", &a, &b);
int t = d[a][b];
if (t > INF / 2) puts("impossible");
else printf("%d\n", t);
}
return 0;
}
(2) 信使
战争时期,前线有 n 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。
信使负责在哨所之间传递信息,当然,这是要花费一定时间的(以天为单位)。
指挥部设在第一个哨所。
当指挥部下达一个命令后,指挥部就派出若干个信使向与指挥部相连的哨所送信。
当一个哨所接到信后,这个哨所内的信使们也以同样的方式向其他哨所送信。信在一个哨所内停留的时间可以忽略不计。
直至所有 n 个哨所全部接到命令后,送信才算成功。
因为准备充足,每个哨所内都安排了足够的信使(如果一个哨所与其他 k 个哨所有通信联系的话,这个哨所内至少会配备 k 个信使)。
现在总指挥请你编一个程序,计算出完成整个送信过程最短需要多少时间。
输入格式
第 1 行有两个整数 n 和 m,中间用 1 个空格隔开,分别表示有 n 个哨所和 m 条通信线路。
第 2 至 m+1 行:每行三个整数 i、j、k,中间用 1 个空格隔开,表示第 i 个和第 j 个哨所之间存在 双向 通信线路,且这条线路要花费 k 天。
输出格式
一个整数,表示完成整个送信过程的最短时间。
如果不是所有的哨所都能收到信,就输出-1。
数据范围
1≤n≤100,
1≤m≤200,
1≤k≤1000
输入样例:
4 4
1 2 4
2 3 7
2 4 1
3 4 6
输出样例:
11
代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, INF = 1e9;
int n, m, Q;
int d[N][N];
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
while(m--){
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = d[b][a]= min(d[a][b], c);
}
floyd();
int res = 0;
for (int i = 1; i <= n; i ++ )
if (d[1][i] == INF)
{
res = -1;
break;
}
else res = max(res, d[1][i]);
cout << res << endl;
return 0;
}
总结:n比较小,故可用
(3)牛的旅行
农民John的农场里有很多牧区,有的路径连接一些特定的牧区。
一片所有连通的牧区称为一个牧场。
但是就目前而言,你能看到至少有两个牧区不连通。
现在,John想在农场里添加一条路径(注意,恰好一条)。
一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。
考虑如下的两个牧场,每一个牧区都有自己的坐标:
1.png
图 1 是有 5 个牧区的牧场,牧区用“*”表示,路径用直线表示。
图 1 所示的牧场的直径大约是 12.07106, 最远的两个牧区是 A 和 E,它们之间的最短路径是 A-B-E。
图 2 是另一个牧场。
这两个牧场都在John的农场上。
John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的牧场有最小的直径。
注意,如果两条路径中途相交,我们不认为它们是连通的。
只有两条路径在同一个牧区相交,我们才认为它们是连通的。
现在请你编程找出一条连接两个不同牧场的路径,使得连上这条路径后,所有牧场(生成的新牧场和原有牧场)中直径最大的牧场的直径尽可能小。
输出这个直径最小可能值。
输入格式
第 1 行:一个整数 N, 表示牧区数;
第 2 到 N+1 行:每行两个整数 X,Y, 表示 N 个牧区的坐标。每个牧区的坐标都是不一样的。
第 N+2 行到第 2*N+1 行:每行包括 N 个数字 ( 0或1 ) 表示一个对称邻接矩阵。
例如,题目描述中的两个牧场的矩阵描述如下:
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
输入数据中至少包括两个不连通的牧区。
输出格式
只有一行,包括一个实数,表示所求答案。
数字保留六位小数。
数据范围
1≤N≤150,
0≤X,Y≤105
输入样例:
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
输出样例:
22.071068

代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define x first
#define y second
using namespace std;
const int N = 200;
typedef pair<double,double> PDD;
const double INF = 1e20;
int n;
PDD q[N];
double d[N][N];
double maxd[N];
char g[N][N];
double get_distance(PDD a,PDD b)
{
double dx = a.x - b.x;
double dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
int main()
{
cin >> n;
for(int i=0;i<n;i++)cin>>q[i].x>>q[i].y;
for(int i=0;i<n;i++)cin>>g[i];
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
if (i == j) d[i][j] = 0;
else if (g[i][j] == '1') d[i][j] = get_distance(q[i], q[j]);
else d[i][j] = INF;
for(int k=0;k<n;k++)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
}
}
double r1=0;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(d[i][j]<INF/2)
{
maxd[i]=max(maxd[i],d[i][j]);
}
}
r1=max(r1,maxd[i]);
}
double r2=INF;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(d[i][j]>INF/2)
{
r2=min(r2,maxd[i]+maxd[j]+get_distance(q[i], q[j]));
}
}
}
printf("%.6lf",max(r1,r2));
return 0;
}
(4)排序
给定 n 个变量和 m 个不等式。其中 n 小于等于 26,变量分别用前 n 的大写英文字母表示。
不等式之间具有传递性,即若 A>B 且 B>C,则 A>C。
请从前往后遍历每对关系,每次遍历时判断:
如果能够确定全部关系且无矛盾,则结束循环,输出确定的次序;
如果发生矛盾,则结束循环,输出有矛盾;
如果循环结束时没有发生上述两种情况,则输出无定解。
输入格式
输入包含多组测试数据。
每组测试数据,第一行包含两个整数 n 和 m。
接下来 m 行,每行包含一个不等式,不等式全部为小于关系。
当输入一行 0 0 时,表示输入终止。
输出格式
每组数据输出一个占一行的结果。
结果可能为下列三种之一:
如果可以确定两两之间的关系,则输出 “Sorted sequence determined after t relations: yyy…y.”,其中’t’指迭代次数,’yyy…y’是指升序排列的所有变量。
如果有矛盾,则输出: “Inconsistency found after t relations.”,其中’t’指迭代次数。
如果没有矛盾,且不能确定两两之间的关系,则输出 “Sorted sequence cannot be determined.”。
数据范围
2≤n≤26,变量只可能为大写字母 A∼Z。
输入样例1:
4 6
A<B
A<C
B<C
C<D
B<D
A<B
3 2
A<B
B<A
26 1
A<Z
0 0
输出样例1:
Sorted sequence determined after 4 relations: ABCD.
Inconsistency found after 2 relations.
Sorted sequence cannot be determined.
输入样例2:
6 6
A<F
B<D
C<E
F<D
D<E
E<F
0 0
输出样例2:
Inconsistency found after 6 relations.
输入样例3:
5 5
A<B
B<C
C<D
D<E
E<A
0 0
输出样例3:
Sorted sequence determined after 4 relations: ABCDE.
代码
传递闭包 O(mn3)O(mn3)
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 26;
int n, m;
bool g[N][N], d[N][N];
bool st[N];
void floyd()
{
memcpy(d, g, sizeof d);
for (int k = 0; k < n; k ++ )
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
d[i][j] |= d[i][k] && d[k][j];
}
int check()
{
for (int i = 0; i < n; i ++ )
if (d[i][i])
return 2;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < i; j ++ )
if (!d[i][j] && !d[j][i])
return 0;
return 1;
}
char get_min()
{
for (int i = 0; i < n; i ++ )
if (!st[i])
{
bool flag = true;
for (int j = 0; j < n; j ++ )
if (!st[j] && d[j][i])
{
flag = false;
break;
}
if (flag)
{
st[i] = true;
return 'A' + i;
}
}
}
int main()
{
while (cin >> n >> m, n || m)
{
memset(g, 0, sizeof g);
int type = 0, t;
for (int i = 1; i <= m; i ++ )
{
char str[5];
cin >> str;
int a = str[0] - 'A', b = str[2] - 'A';
if (!type)
{
g[a][b] = 1;
floyd();
type = check();
if (type) t = i;
}
}
if (!type) puts("Sorted sequence cannot be determined.");
else if (type == 2) printf("Inconsistency found after %d relations.\n", t);
else
{
memset(st, 0, sizeof st);
printf("Sorted sequence determined after %d relations: ", t);
for (int i = 0; i < n; i ++ ) printf("%c", get_min());
printf(".\n");
}
}
return 0;
}
增量算法 O(mn2)O(mn2)
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 26;
int n, m;
bool d[N][N];
bool st[N];
int check()
{
for (int i = 0; i < n; i ++ )
if (d[i][i])
return 2;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < i; j ++ )
if (!d[i][j] && !d[j][i])
return 0;
return 1;
}
char get_min()
{
for (int i = 0; i < n; i ++ )
if (!st[i])
{
bool flag = true;
for (int j = 0; j < n; j ++ )
if (!st[j] && d[j][i])
{
flag = false;
break;
}
if (flag)
{
st[i] = true;
return 'A' + i;
}
}
}
int main()
{
while (cin >> n >> m, n || m)
{
memset(d, 0, sizeof d);
int type = 0, t;
for (int i = 1; i <= m; i ++ )
{
char str[5];
cin >> str;
int a = str[0] - 'A', b = str[2] - 'A';
if (!type)
{
d[a][b] = 1;
for (int x = 0; x < n; x ++ )
{
if (d[x][a]) d[x][b] = 1;
if (d[b][x]) d[a][x] = 1;
for (int y = 0; y < n; y ++ )
if (d[x][a] && d[b][y])
d[x][y] = 1;
}
type = check();
if (type) t = i;
}
}
if (!type) puts("Sorted sequence cannot be determined.");
else if (type == 2) printf("Inconsistency found after %d relations.\n", t);
else
{
memset(st, 0, sizeof st);
printf("Sorted sequence determined after %d relations: ", t);
for (int i = 0; i < n; i ++ ) printf("%c", get_min());
printf(".\n");
}
}
return 0;
}
**只需要把能更新的更新就行,不需要重新做一遍floyd,提高效率**

