概念
连通图的⽣生成树定义:
所谓⼀个连通图的⽣成树是一个极小的连通子图,它含有图中全部的n个顶点,但只足以
构成一颗树的n-1条边.
定义解读:
满⾜以下3个条件则为连通图的生成树:
1.图是连通图;
2.图中包含了了N个顶点;
3.图中边的数量量等于N-1条边.
最小⽣成树: 把构成连通网的最⼩代价的生成树称为最⼩⽣成树。

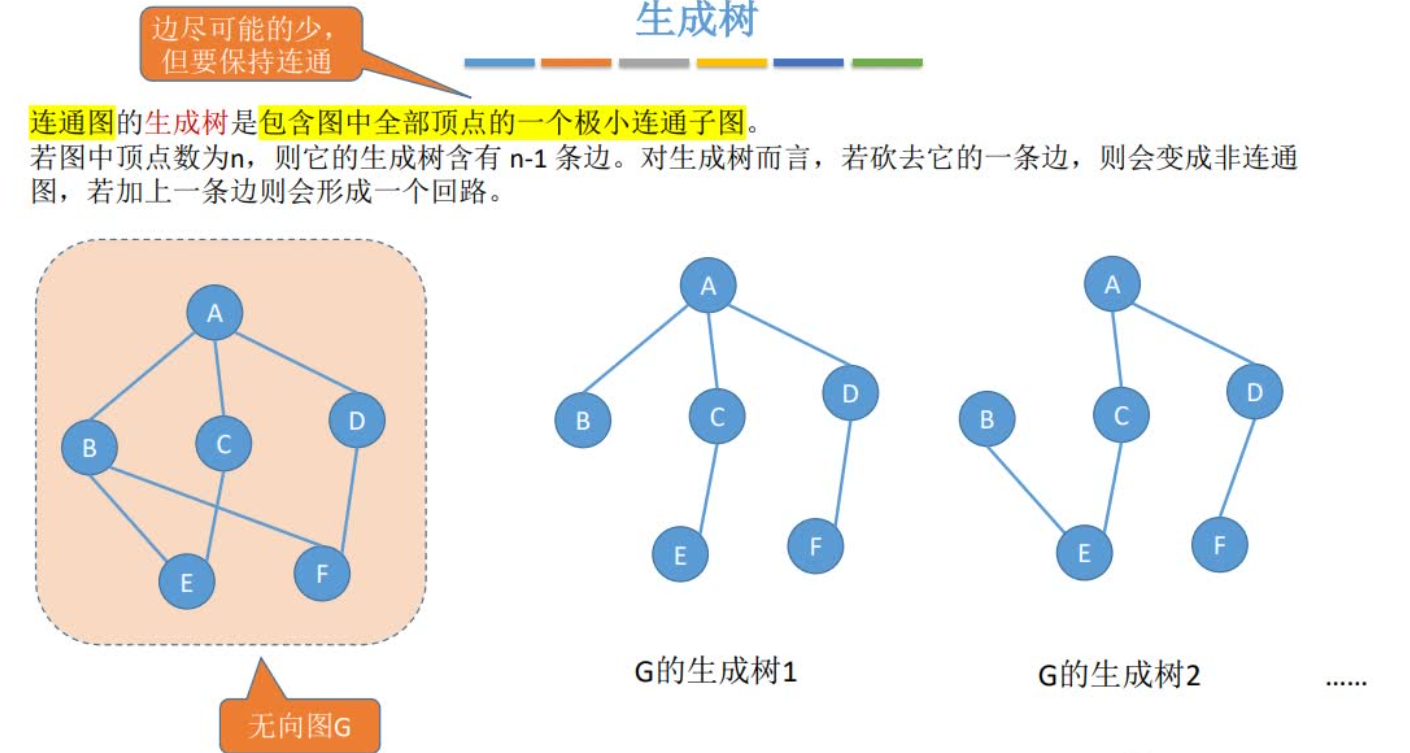
广度优先生成树

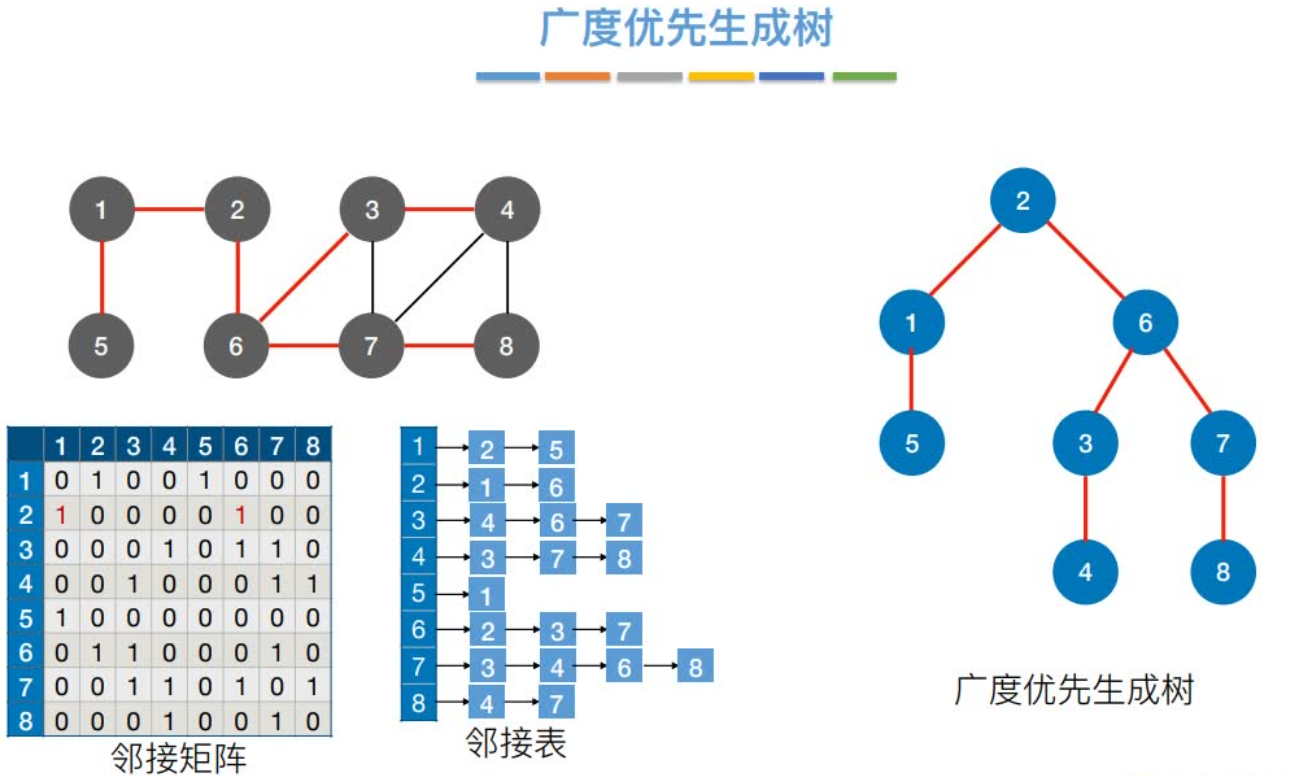
深度优先生成树

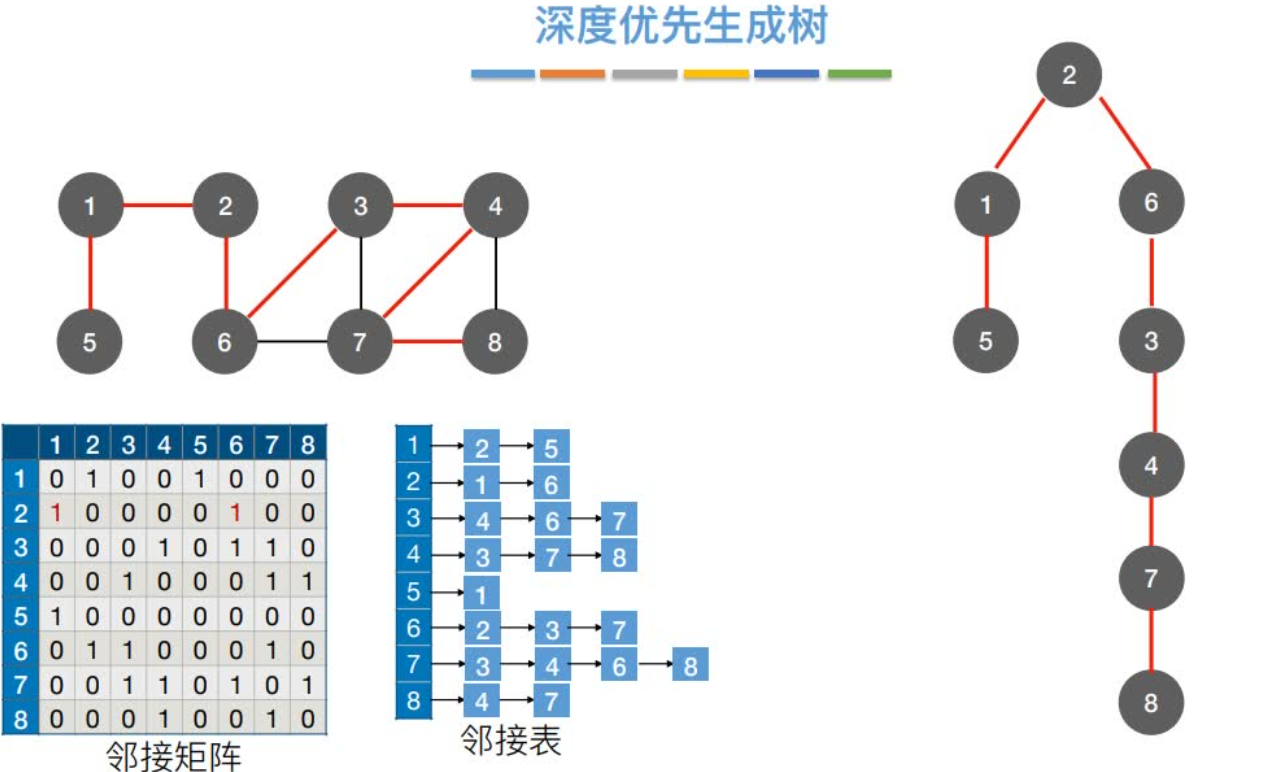
最⼩⽣成树（最⼩代价树）


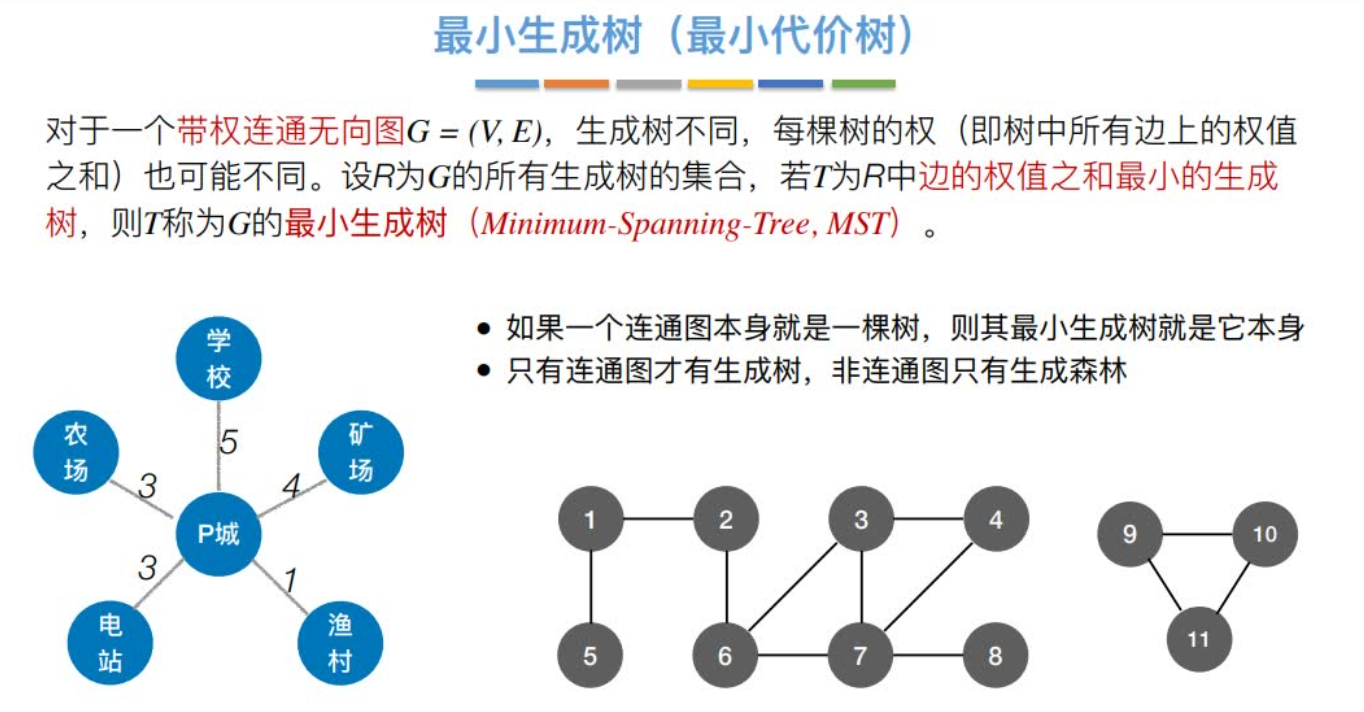
对于⼀个带权连通⽆向图
G = (V, E)，⽣成树不同，每棵树的权（即树中所有边上的权值之和）也可能不同。设R为G的所有⽣成树的集合，若T为R边的权值之和最⼩的⽣成树，则T称为G的最⼩⽣成树（Minimum-Spanning-Tree, MST）。
•最⼩⽣成树可能有多个，但边的权值之和总是唯⼀且最⼩的
•最⼩⽣成树的边数 = 顶点数 - 1。砍掉⼀条则不连通，增加⼀条边则会出现回路
•如果⼀个连通图本身就是⼀棵树，则其最⼩⽣成树就是它本身
•只有连通图才有⽣成树，⾮连通图只有⽣成森林
Prim 算法（普⾥姆）
Prim算法（普⾥姆）：从某⼀个顶点开始构建⽣成树；每次将代价最⼩的新顶点纳⼊⽣成树，直到所有顶点都纳⼊为⽌。
算法思路以及步骤
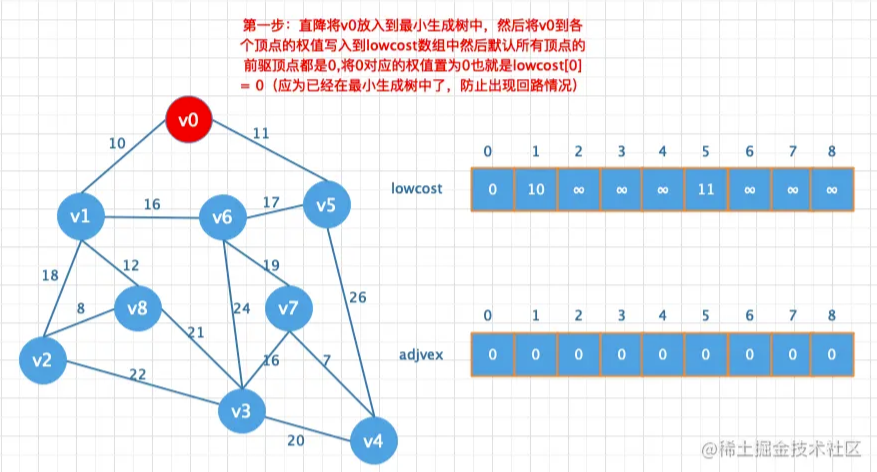
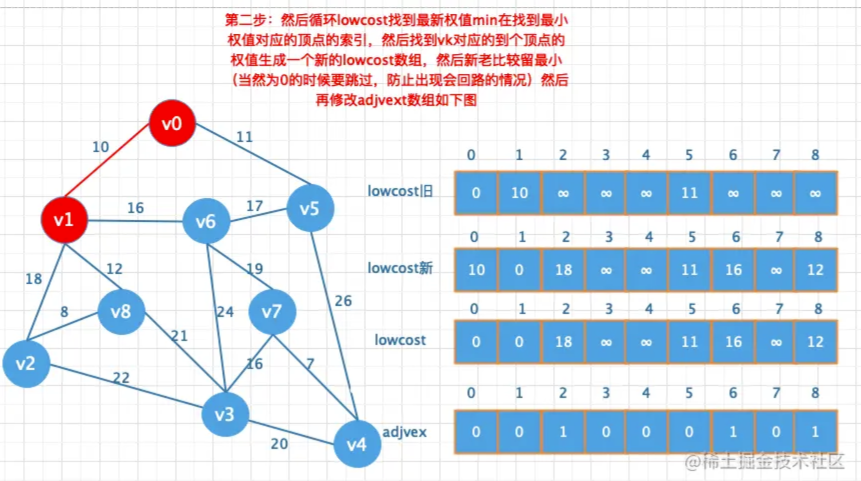
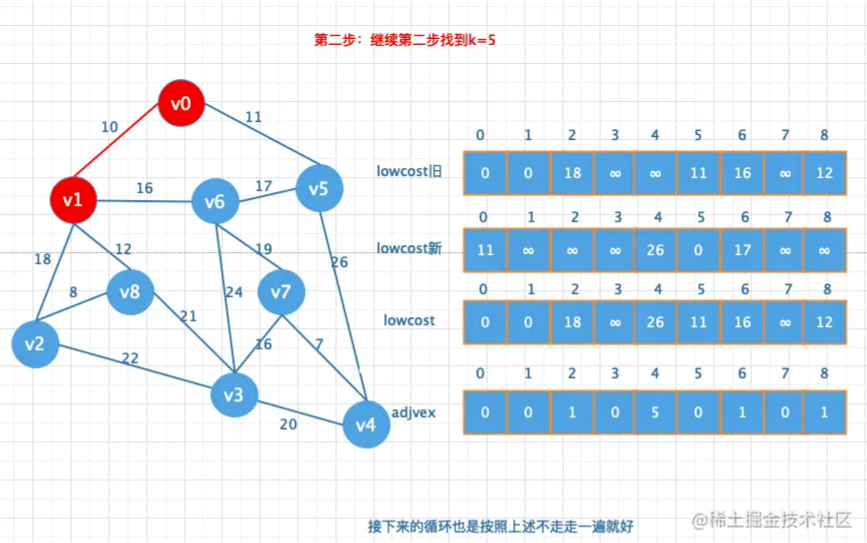
大概的思路就是循环一个一个找，先找到v0到所有结点的前置记录下来，如果不能直接到达的权值设置为无穷大，这时候可以将0这个位置的下标j记为0 表示0位置这个顶点已经加入到最小生成树中了，然后遍历lowcost数组找到权值最小的顶点索引，再将该顶点对应到每个顶点的权值（已经加入到最小生成树的顶点除外）和lowcost数组中的前置进行对比如果更小更新lowcost数组的值然后再更新adjvex数组的值(如果是连通图的话冲一个顶点出发循环（顶点个数）次数，刚好吧图整个都遍历了一遍)
步骤：
1.创建两个数组lowcost和adjvex数组，lowcost用于存储权值，adjvex用来存储当前顶点的前驱顶点索引
2.遍历所有顶点，并将对应的权值和索引写入到对应的数组
3.最后的到的adjvex索引数组就是得出的最小生成树
图解



Kruskal 算法（克鲁斯卡尔）
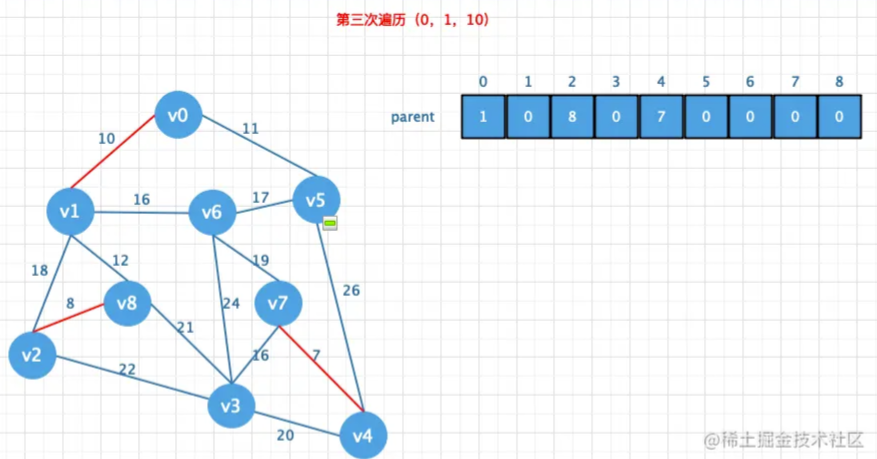
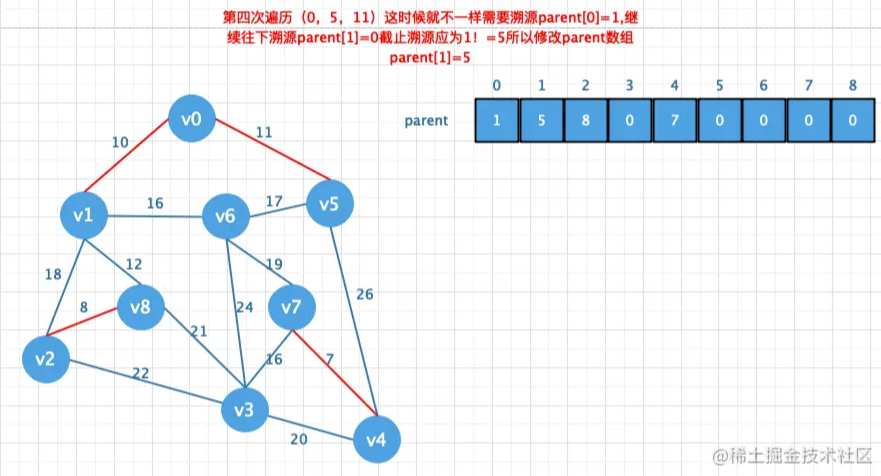
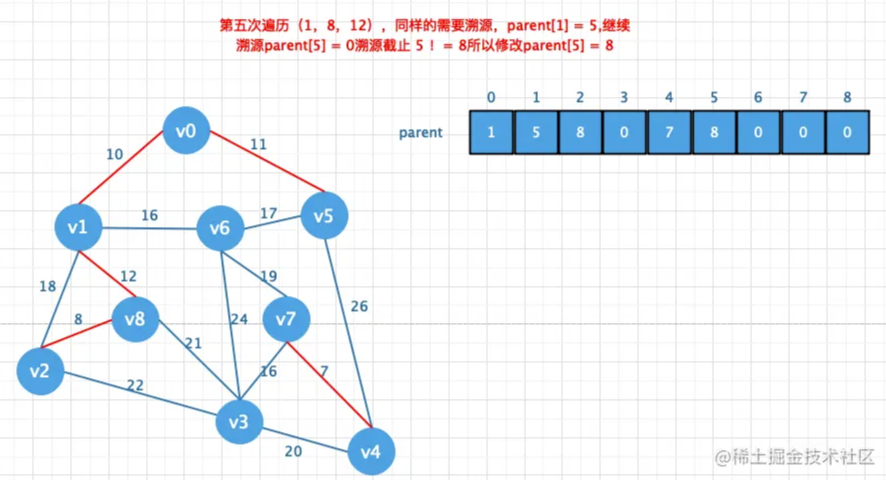
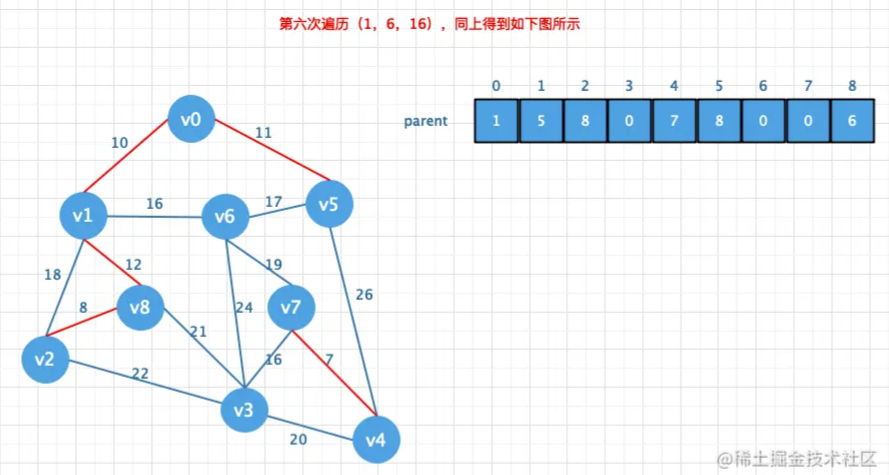
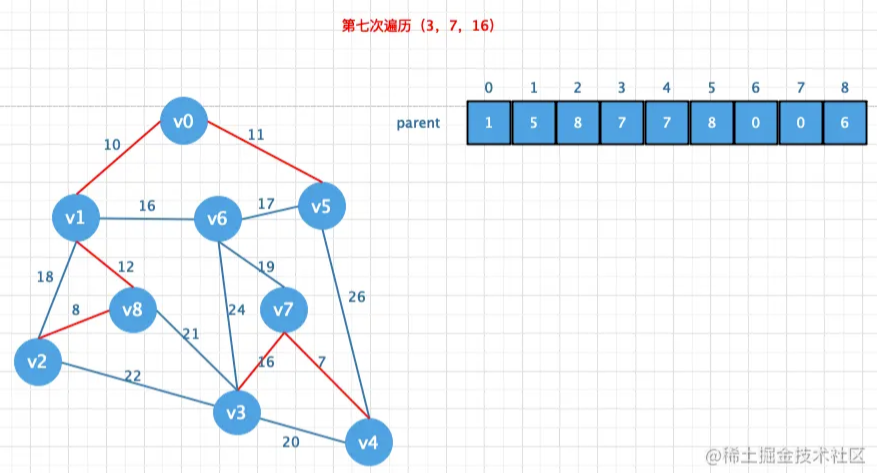
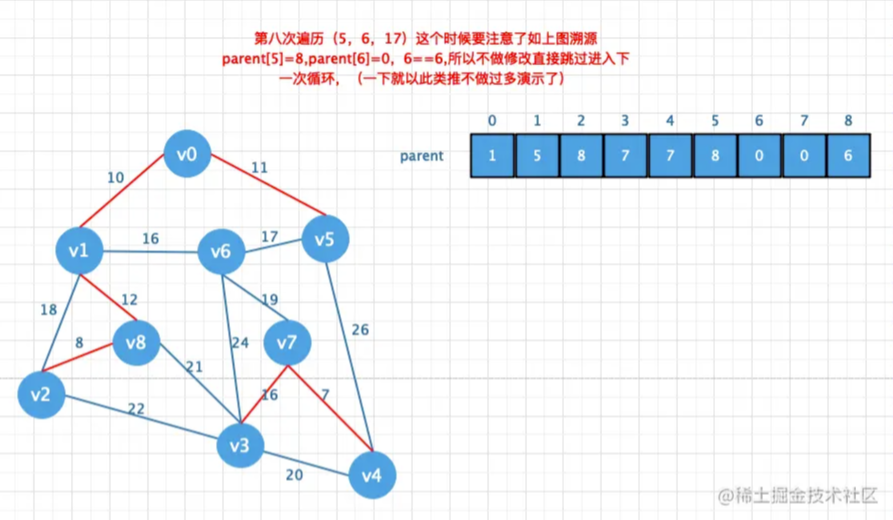
Kruskal算法：每次选择⼀条权值最⼩的边，使这条边的两头连通（原本已经连通的就不选）直到所有结点都连通
算法思路
首先要将邻接矩阵转换成边表数组，然后将边表数组的权值冲小到大排列，
然后再创建一个parent数组用来存放结点的父节点,然后遍历所有的边，通过parent
数组找到对应的对应边的链接信息避免闭环问题.如果不存在闭环则添加到最小生
成树中（也就是将对应的值存储在parent数组中）
这个算法的精髓就是按照边表顺序从小到大一个边一个边的组合。只要组合成了一个生成树
那这时候的生成树就是最小生成树
图解










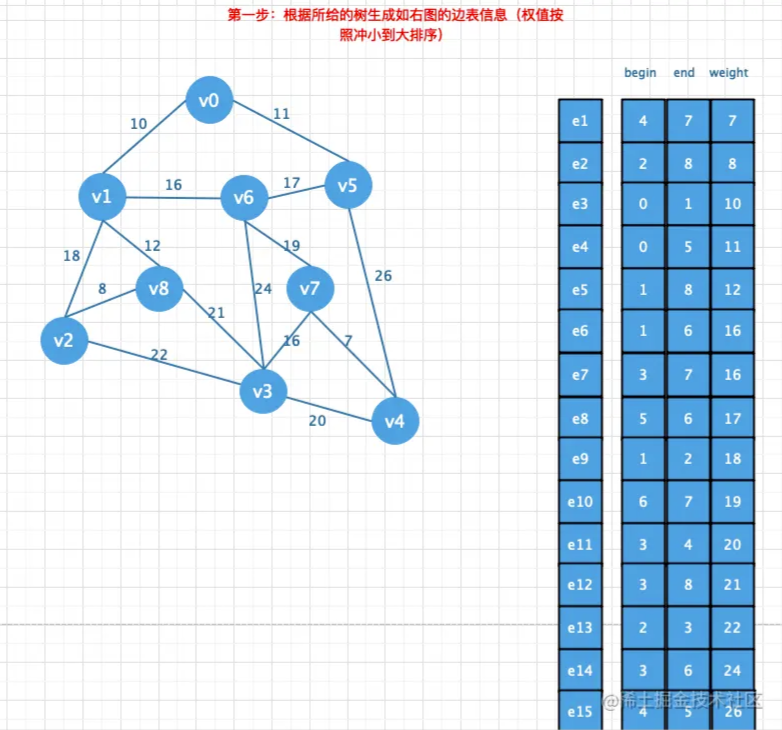
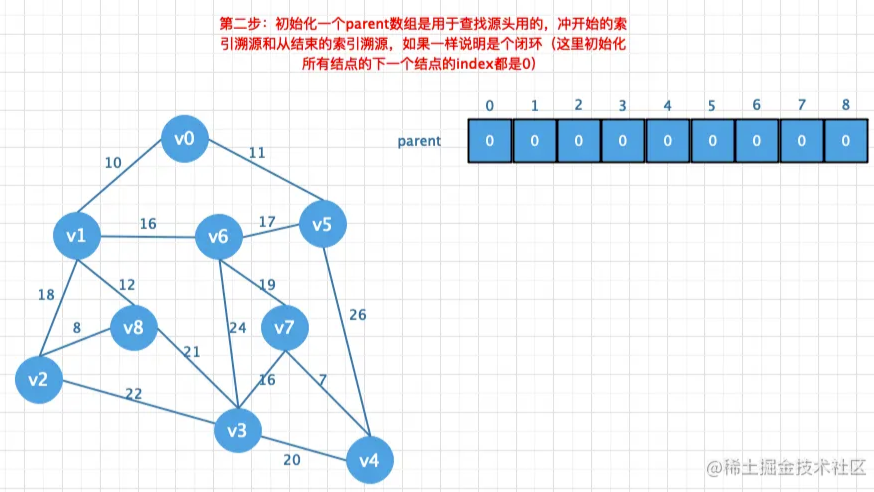
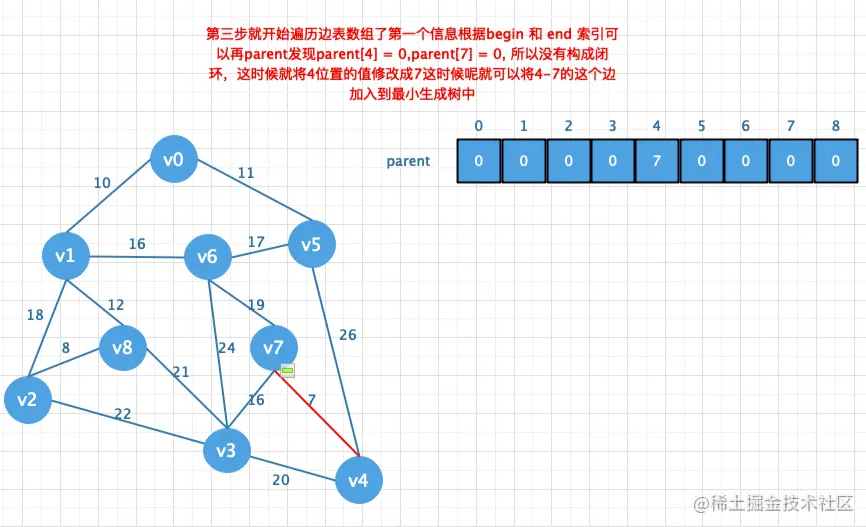
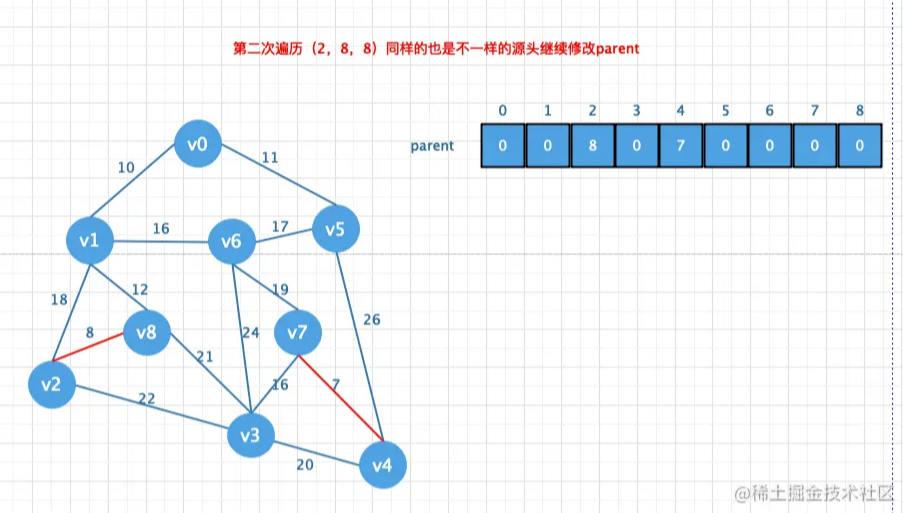
对比

代码实现参考
https://blog.csdn.net/m0_46202433/article/details/106614431