动态规划专题

$1.$ 前言

提醒！作者曾经对动态规划理解有误，如果您曾经被误导，我道歉。

$DP$ 的核心思想是用集合来表示一类方案，然后从集合的独立参数来考虑状态之间的递推关系。

所有DP问题都可以从集合角度来解释。一般的DP问题都是在有限集合内求最值或求个数，极个别的DP问题会在无限集合内求最值，此时先将无限集想办法缩小到有限集即可

$2.$ 原理

动态规划 将 待求解问题 分解成若干个 子问题，先求解子问题，然后由这些子问题的解扩展为 原问题的解，是一种 多阶段决策问题。

阶段是不同的子问题，状态是子问题的答案。

决策是什么 根据的是状态，集合的属性 是指 动态规划中状态的属性。

在实际问题中，阶段是子问题的求解过程，完成了 前一阶段的计算 之后才会执行 下一阶段的计算。

所以阶段 不能转移，能转移的是状态，而转移的方式叫 决策。

阶段没有值，只有状态有值，所以$f$数组里存的都是状态。

阶段存在的意义是便于写出转移方程。

定义状态技巧

结合模型 来辨认，这需要从模型的最本质特征来看。

对于难以表示子问题的题目，考虑用 记忆化搜索 转移。

状态的设计必须要能计算出答案，如果有多维信息，可能就要开多维数组。

它必须可以表示所有子问题的答案，如果改变某数据子问题会有变化，状态设计就要加入这类数据。

这主要是 从最后一步决策来分析。

我们可以将产生后效性的东西放入状态中，

比如说在乌龟棋中，当前用掉的牌可能导致之后没有牌用，不符合子结构最优。

如果你只是设计为用了几个牌/开四格数组，则无法通过下标表示不同子结构的情况。

这告诉我们，导致后效性的值，一定是用 下标 表示。

朴素想法是设计阶段为走到那个点且用了什么牌。

部分题目会出现状态难以转移，但又不属于上面三种情况。

这就要用 状态机思想，其本质就是将 阶段分化，达到简化目的。

一般来说，你能将阶段拆成几部分，就加几格（维）数组。

拆分的方法是找到子问题间有什么关系时会转移、以及会转移到哪几个不同的阶段。

或者说提取其中的独立参数。

通常这几格数组的作用有

1.从实际情况出发，对参数进行细分。

2.从实际情况出发，维护不同类型且可相互转移的信息。

3.可以完全维护状态数组转移的条件或信息。

化简状态技巧

表示等价法（状态信息间可以互相表示）

贪心法（$LIS$）

$hash$ 预处理法（拒绝挨个比较，我们要直接跳）

状态压缩法

更换费用法（背包）

数学化简法（背包）

状态转移要点

动态规划的转移是空间上从小往大、时间上从短往长转移。

记忆化搜索是将原问题拆成子问题后解决并融合出答案。

状态转移前一定要找到 初态，这通常是它 最初转移的层数。

对于错误的层数，我们要初始化避免转移（部分题目可以不初始化）

比起美观的表示，更重要的是考虑下标边界值的程序，不能因为某些层不被答案需要就不转移了。

记忆化搜索 的 边界 通常要看它的 参数（描述的问题大小）。

在方案数类型的计算中，

要先确认转移（合并）时要用的是 加法原理（并列） 还是 乘法原理（递进）。

状态转移优化

找出数据的性质，运用 优化模型。

观察方程的概况，联系化简。

找出状态的共同点，用数组维护，即对于有 相同参数的状态 可以提出来用新数组维护。

$3.$ 整理

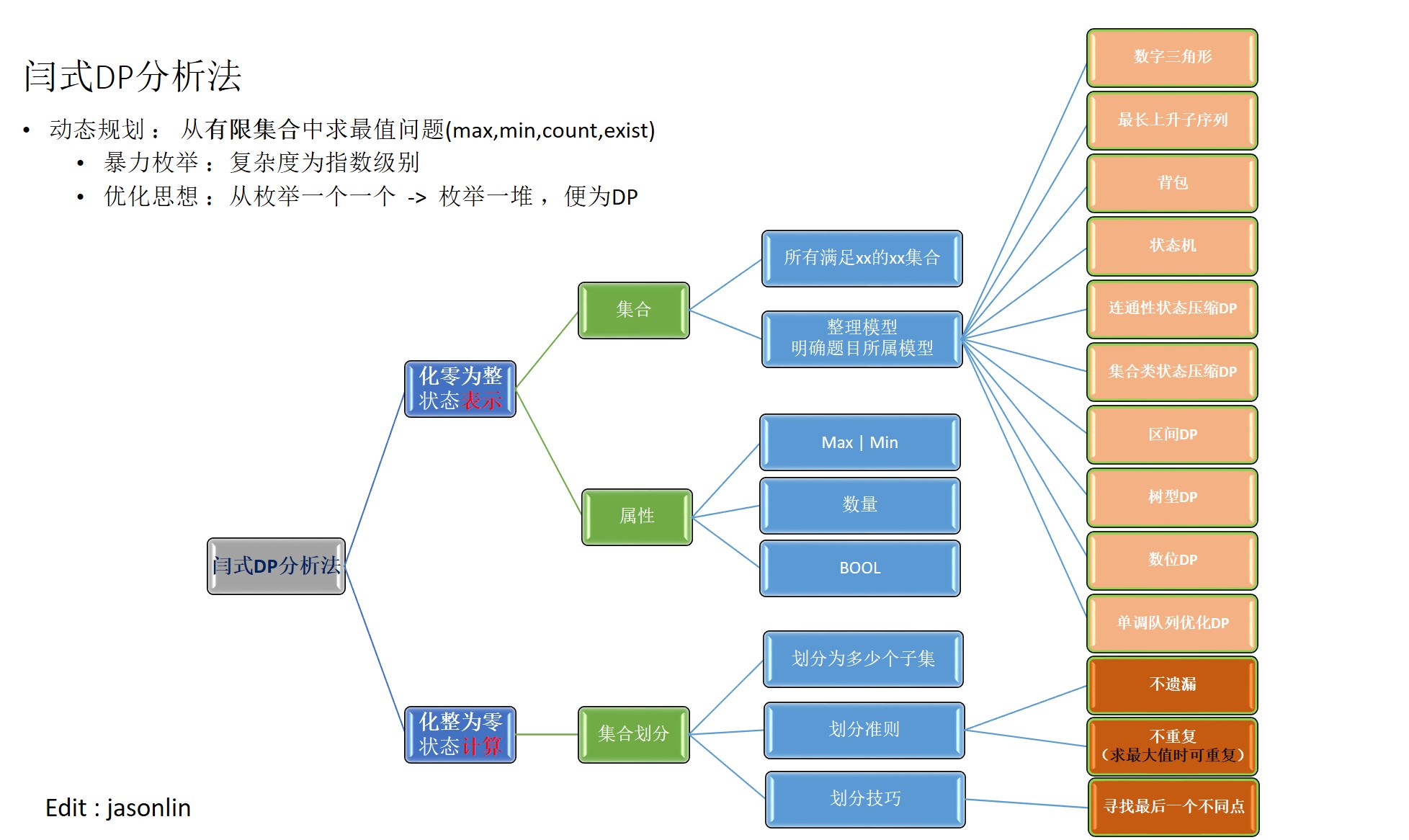
解释一下集合划分那一版块的几个要点，顺带进行修正。

• 求最大最小值时都可以重复

• 分析法刻画的是从哪些状态转移

$4.$ 无限集

我们上面的分析都有一个 隐形的要求，即 无论阶段还是状态 都必须是 有限的。

也就是在 有限集合 中求最值问题，若 集合是无限的，则需要我们对其进行 贪心 或 数学确认上界。

贪心+数学证明：【例题 1】分级

数学：【例题 2】货币系统

$5.$ 滚动数组

根据上文，我们知道 动态规划的阶段 之间满足 无后效性，

因此我们不需要 储存 所有的阶段，而只需要 储存 与 当前阶段 有关联的阶段，

这可以用 动态存储 的方式进行优化。

$6.$ 单调性

常见的单调性优化有四种 二分优化、倍增优化、单调队列优化、平衡树优化。

其中 二分、倍增优化 要求数据一定满足 单调性。

而 单调队列、平衡树优化 则可以自主建立 单调性。

单调队列 可维护 区间最值 、单顺序的区间最差 等信息。

单调栈 可维护 所有连续上升、下降子序列的位置与长度。