大家好哇,我又来学数据结构了。
参考资料:
前置芝士:
-
线段树(废话)
-
动态开点
-
亿点树上问题基础
线段树合并
顾名思义,我们要把两颗线段树合并在一起,如图
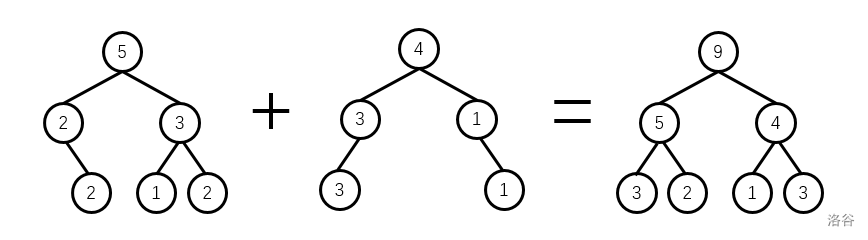
(假设我们要维护的是权值和的信息,维护其他信息只需要稍作更改)
实现起来很简单,我们只需要把对应位置相加起来就行了。
//稍微改了下马蜂(
void merge(int &x,int y) {
if(!x||!y) x|=y;
else {
tre[x].val+=tre[y].val;
merge(ls(x),ls(y));
merge(rs(x),rs(y));
}
}
为了节省空间不开新点,直接将 y 树合并到 x 树上,但这样做的前提是在之后的操作中,y 树不会再出现。因为我们直接合并的话,x 和 y 树是共用一个结点的,如果对其中一棵树有更改,会对另一棵树有影响。因此,如果 y 树合并后还会再出现,建议新开点存合并后的树。
有人问,这两次递归都调用了,时间复杂度不是 $O(n)$ 的嘛?
不是的,是 $O(\log n)$,证法有点玄学,窝不会(
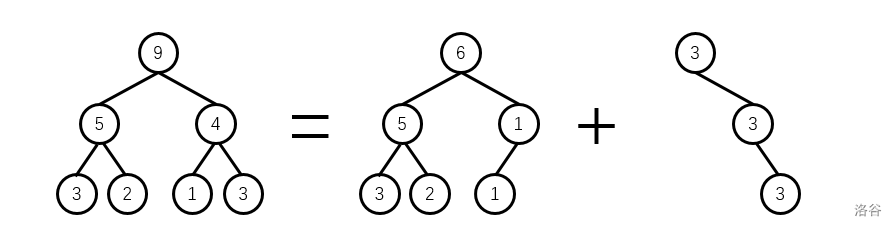
线段树分裂
顾名思义,就是合并反过来操作。线段树的分裂,有按权值分裂和按区间分裂(怎么一股 fhq 的味道),这里依次讲解。
按权值分裂(按 $k$ 小分裂)
void split(int x,int &y,int k) {//x为原(子)树,分裂后为前k小的树,y为剩下的树
y=++cnt;int val=tre[ls(x)].val;
if(k>v) split(rs(x),rs(y),k-v);
else swap(rs(x),rs(y));
if(k<v) split(ls(x),ls(y),k);
tre[y].val=tre[x].val-k;
tre[x].val=k;
}
这里我们分情况讨论:($v$ 为左子树的权值/大小)
-
当 $v<k$ 时,左子树给 $x$ 不用处理,直接分裂右子树。
-
当 $v\ge k$ 时,右边归 $y$ ,
swap一下就行。 -
当 $v>k$ 时,还需要递归左边。
最后将权值赋值一下就行。
按区间分裂
很简单,像普通线段树一样,把区间剖出来就行了。
inline void pushup(int p) {tre[p].val=tre[ls(p)].val+tre[rs(p)].val;}
int split(int &p,int l,int r,int L,int R) {//l,r为原(子)树区间,L,R为剖出来的区间
int now=++cnt;
if(L<=l&&r<=R) {
tre[now]=tre[p];
p=0;return now;
}
int mid=l+r>>1;
if(L<=mid) ls(now)=split(ls(p),l,mid,L,R);
if(R>mid) rs(now)=split(rs(p),mid+1,r,L,R);
pushup(p);pushup(now);
return now;
}
如果原树区间被覆盖,则直接搞出来就行,把原树置为 $0$。
否则按普通线段树一样递归,记得更新信息。

