历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

搜索算法学习笔记

作者：

RuntimeErr , 2022-02-09 21:48:44 , 所有人可见 , 阅读 328

3

3

此笔记始于 $2021.4.3$，蒟蒻在 $AcWing$ 学习搜索算法（QAQ没有打广告啊）

不得不说，搜索和图论绝对是考场上极大概率会出的考点，之后学习图论时会增加图论学习笔记。

$BFS$ 特点

求最小：这个不用说了吧
基于迭代：相比于 $DFS$ 来说不会爆栈

所以当遇到一个问题同时可以用 $BFS$ 和 $DFS$ 求解的时候，当然是优先选择 $BFS$ 。

$Flood\ Fill$ 模型

模型介绍：

所谓 $FloodFill$ ，顾名思义，洪水覆盖，具体什么意思呢，可以理解成连通块问题，或是您在 $Minecraft$ 的平地上放一桶水（，水不会流到障碍物，而是向四周的平地继续扩散。

$Flood\ Fill$ 不一定只是基于 $BFS$，但最好要选择 $BFS$，因为我上面说过了，$DFS$ 可能会导致爆栈。

那么它有什么作用呢？它的作用就是在线性时间复杂度内找到某个点所在连通块

话不多说，上例题：P1596 [USACO10OCT]Lake Counting S

$Description$：

农夫约翰有一片 $N\times M$ 的矩形土地。

最近，由于降雨的原因，部分土地被水淹没了。

现在用一个字符矩阵来表示他的土地。

每个单元格内，如果包含雨水，则用 ”$W$” 表示，如果不含雨水，则用”.”表示。

现在，约翰想知道他的土地中形成了多少片池塘。

每组相连的积水单元格集合可以看作是一片池塘。

每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。

请你输出共有多少片池塘，即矩阵中共有多少片相连的 ”$W$” 块。

$Solution:$

这道题是 $Flood\ Fill$ 算法的典型应用。我们可以逐行扫描整个字符矩阵，当找到一处有水的土地，且还没有被标记（即覆盖）时，从这个点开始做 $Flood\ Fill$ ：标记其所在的整个连通块并增加答案。也可以这么说：我们在一片茫茫大海上航行，当我们发现一片新大陆时，我们把整个大陆都探索一遍，再继续寻找其他大陆，直到全世界都走了个遍。这也是 $Flood\ Fill$ 的核心思想。

是不是很简单呢，这里直接给出代码：

$Code:$

#include<cstdio>
#include<queue>
using namespace std;
const int N=110;
typedef pair<int,int> p;
#define mp(x,y) make_pair(x,y)
#define x first
#define y second

int n,m,ans,f[8][2]={{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
bool vis[N][N];
queue<p>q;

void bfs(int i,int j){//标记连通块操作，代码不难理解
    q.push(mp(i,j));
    vis[i][j]=true;
    while(!q.empty()){
        p tmp=q.front();q.pop();
        int xx,yy;
        for(int i=0;i<8;++i){
            xx=tmp.x+f[i][0],yy=tmp.y+f[i][1];
            if(xx<=0||xx>n||yy<=0||yy>m||vis[xx][yy])continue;
            vis[xx][yy]=true;
            q.push(mp(xx,yy));
        }
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            char t;scanf(" %c",&t);
            vis[i][j]=t=='.';//不用搜的提前标记
        }
    }
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            if(!vis[i][j]){//如果有没发现的新大陆
                ++ans;//答案增加
                bfs(i,j);//标记整个连通块
            }
        }
    }
    printf("%d",ans);
    return 0;
}

再来看一道例题 P1457 [USACO2.1]城堡 The Castle

$Description$：

    1   2   3   4   5   6   7  
   #############################
 1 #   |   #   |   #   |   |   #
   #####---#####---#---#####---#
 2 #   #   |   #   #   #   #   #
   #---#####---#####---#####---#
 3 #   |   |   #   #   #   #   #
   #---#########---#####---#---#
 4 #   #   |   |   |   |   #   #
   #############################
           (图 1)

   #  = Wall   
   |  = No wall
   -  = No wall

   方向：上北下南左西右东。

如图是一个城堡的地形图。

请你编写一个程序，计算城堡一共有多少房间，最大的房间有多大，移除一面墙能得到的最大的房间的大小，移除哪面墙可以得到面积最大的新房间。

城堡被分割成 $m\times n$ 个方格区域，每个方格区域可以有 $0-4$ 面墙。

注意：墙体厚度忽略不计，选择最佳的墙来推倒。有多解时选最靠西的，仍然有多解时选最靠南的。同一格子北边的墙比东边的墙更优先。

$Solution:$

先来解释一下样例吧，如图

我们可以找出，一共有 $5$ 个房间，最大的房间面积为 $9$ ，移去箭头所指的那面墙，可以使 $2$ 个房间合为一个新房间，且比移去其他墙所形成的房间都大。

这道题难就难在输入，每一个单位的数字告诉我们这个单位的东西南北是否有墙存在。每个数字是由以下四个整数中的任意个加起来的。

$1:$ 在西面有墙

$2:$ 在北面有墙

$4:$ 在东面有墙

$8:$ 在南面有墙

即若输入是 $11$，$11=1+2+8$，则代表这个格子西、北、东都有墙。

我们发现，代表墙的四个数都是 $2^k$，所以直接二进制枚举就行了，用 $0,1,2,3$ 分别表示西、北、东、南（即 $2^k$ 的 $k$）。

前两问很简单，房间个数就是连通块个数，最大面积也可以在 $BFS$ 的时候计算，主要是后两问，我们把前后两问单独拿出来计算。

我们在前两问的 $BFS$ 中可以预处理出每个点所在的连通块，和所在连通块的大小，那么回答完前两个问题后再枚举一遍整个矩阵，找到有墙且墙两边的房间不属于同一连通块的位置，比较两边连通块大小的和和当前答案即可。

！！！注意细节——“有多解时选最靠西的，仍然有多解时选最靠南的。同一格子北边的墙比东边的墙更优先”，枚举时注意顺序。

$Code:$

#include<cstdio>
#include<queue>
#include<iostream>
using namespace std;

const int N=55;
typedef pair<int,int> p;
#define mp(x,y) make_pair(x,y)
#define x first
#define y second

int n,m;
int cnt,ans1,ans2,ansx,ansy;char direction;//连通块个数，最大面积，推掉一面墙的最大面积，墙的方位 
int map[N][N],f[4][2]={{0,-1},{-1,0},{0,1},{1,0}};//西，北，东，南（注意顺序）
int vis[N][N],area[N*N];//记录所在连通块,每个连通块面积 
queue<p> q;

void bfs(int i,int j){
    q.push(mp(i,j));vis[i][j]=cnt;
    while(!q.empty()){
        p tmp=q.front();q.pop();
        ++area[cnt];
        for(int i=0;i<4;++i){//2进制枚举
            if(((map[tmp.x][tmp.y]>>i)&1)==0){//如果没有墙（优先级害人啊QAQ）
                int xx=tmp.x+f[i][0],yy=tmp.y+f[i][1];
                if(xx<=0||xx>n||yy<=0||yy>m||vis[xx][yy])continue;
                vis[xx][yy]=cnt;
                q.push(mp(xx,yy));
            }
        }
    }
}

int main(){
    scanf("%d%d",&m,&n);//注意输入是m,n 
    for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&map[i][j]);

    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            if(!vis[i][j]){
                ++cnt;bfs(i,j);
                ans1=max(ans1,area[cnt]);
            }
        }
    }
    printf("%d\n%d\n",cnt,ans1);

    for(int j=1;j<=m;++j){
        for(int i=n;i;--i){//"有多解时选最靠西的，仍然有多解时选最靠南的"
            for(int k=1;k<=2;++k){//枚举北、东两个方向 ,"同一格子北边的墙比东边的墙更优先"
                if((map[i][j]>>k)&1){//如果有墙 
                    int xx=i+f[k][0],yy=j+f[k][1];
                    if(xx<=0||xx>n||yy<=0||yy>m)continue;
                    int sum=area[vis[i][j]]+area[vis[xx][yy]];//加上两个连通块的面积，相同连通块后面判断 
                    if(vis[i][j]^vis[xx][yy]&&sum>ans2){
                        ans2=sum,ansx=i,ansy=j;
                        direction=k==1?'N':'E';
                    }
                }
            }
        }
    }
    printf("%d\n%d %d %c",ans2,ansx,ansy,direction);
    return 0;
}

练习：

P3456 [POI2007]GRZ-Ridges and Valleys

CF510B Fox And Two Dots

最短路模型

模型介绍

这名字不显而易见？不用我讲了呢。我们知道，$BFS$ 有一个很好的性质，就是当所有边的权值都相等的情况下，$BFS$ 第一次搜到某个点的路径就是从源点到这个点的单源最短路径。

那就上例题吧 1076. 迷宫问题（洛谷上找不到相同的题，只好直接放了QAQ，如果有记得告诉我题号啊）

$Description:$

给定一个 n×n 的二维数组，如下所示：

int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

};

它表示一个迷宫，其中的 $1$ 表示墙壁，$0$ 表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

输出从左上角到右下角的最短路线，如果答案不唯一，输出任意一条路径均可。

按顺序，每行输出一个路径中经过的单元格的坐标，左上角坐标为 $(0,0)$，右下角坐标为 $(n-1,n-1)$。

数据保证至少存在一条从左上角走到右下角的路径。

$Solution:$

这用 $BFS$ 显然很好写：我们可以记录一个 $pre[i][j]$ 数组，这个数组是 $pair$ 类型的，干什么用呢？记录一个点是从哪个点搜到的，最后得出答案的时候我们可以得到从终点到起点的一条路径，最后反向输出即可。

小 $trick:$ 我们不妨从终点开始搜回起点，最后把路径“逆序”输出就好了啊。

$Code:$

#include<cstdio>
#include<queue>
using namespace std;

const int N=1e3+10;
typedef pair<int,int> p;
#define mp(x,y) make_pair(x,y)
#define x first
#define y second

int n,map[N][N];bool vis[N][N];
int f[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
p pre[N][N];
queue<p> q;

void bfs(){
    pre[n][n].x=pre[n][n].y=0;//这个是待会输出的终止条件 
    q.push(mp(n,n));//从终点搜回起点
    vis[n][n]=true;
    while(!q.empty()){
        p tmp=q.front();q.pop();
        for(int i=0;i<4;++i){
            int xx=tmp.x+f[i][0],yy=tmp.y+f[i][1];
            if(xx<=0||xx>n||yy<=0||yy>n||vis[xx][yy]||map[xx][yy])continue;
            pre[xx][yy]=tmp;//加入路径 
            vis[xx][yy]=true;
            q.push(mp(xx,yy));
        }
    }
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i){
        for(int j=1;j<=n;++j){
            scanf("%d",&map[i][j]);
        }
    }
    bfs();
    //“逆序”输出 
    puts("0 0");
    p tmp=pre[1][1];
    while(tmp.x&&tmp.y){
        printf("%d %d\n",tmp.x-1,tmp.y-1);//由于我这里是1~n所以要-1 
        tmp=pre[tmp.x][tmp.y];
    }
    return 0;
}

再来看第二道例题 188. 武士风度的牛

$Description:$

农民 $John$ 有很多牛，他想交易其中一头被 $Don$ 称为 $The\ Knight$ 的牛。

这头牛有一个独一无二的超能力，在农场里像 $Knight$ 一样地跳（就是我们熟悉的象棋中马的走法）。

虽然这头神奇的牛不能跳到树上和石头上，但是它可以在牧场上随意跳，我们把牧场用一个 $x,y$ 的坐标图来表示。

这头神奇的牛像其它牛一样喜欢吃草，给你一张地图，上面标注了 $The\ Knight$ 的开始位置，树、灌木、石头以及其它障碍的位置，除此之外还有一捆草。

现在你的任务是，确定 $The\ Knight$ 要想吃到草，至少需要跳多少次。

$The \ Knight$ 的位置用 $K$ 来标记，障碍的位置用 $*$ 来标记，草的位置用 $H$ 来标记。

这里有一个地图的例子：

             11 | . . . . . . . . . .
             10 | . . . . * . . . . . 
              9 | . . . . . . . . . . 
              8 | . . . * . * . . . . 
              7 | . . . . . . . * . . 
              6 | . . * . . * . . . H 
              5 | * . . . . . . . . . 
              4 | . . . * . . . * . . 
              3 | . K . . . . . . . . 
              2 | . . . * . . . . . * 
              1 | . . * . . . . * . . 
              0 ----------------------
                0 1 2 3 4 5 6 7 8 9 10

The Knight 可以按照下图中的 $A,B,C,D…$ 这条路径用 $5$ 次跳到草的地方（有可能其它路线的长度也是 $5$）：

             11 | . . . . . . . . . .
             10 | . . . . * . . . . .
              9 | . . . . . . . . . .
              8 | . . . * . * . . . .
              7 | . . . . . . . * . .
              6 | . . * . . * . . . F<
              5 | * . B . . . . . . .
              4 | . . . * C . . * E .
              3 | .>A . . . . D . . .
              2 | . . . * . . . . . *
              1 | . . * . . . . * . .
              0 ----------------------
                0 1 2 3 4 5 6 7 8 9 10

$Solution:$

这道题除了行走方式不同外都相同，还记得我们上面说的性质嘛，边权相同时，一个点在 $BFS$ 中第一次被搜到的路径一定就是单源最短路径，那么问题就解决啦。

$Code:$

#include<cstdio>
#include<cstdlib>
#include<queue>
using namespace std;

const int N=200;
typedef pair<int,int> p;
#define mp(x,y) make_pair(x,y)
#define x first
#define y second

int r,c,sx,sy,fx,fy;
char map[N][N];
int cnt[N][N];
int f[8][2]={{-2,-1},{-2,1},{-1,2},{1,2},{2,-1},{2,1},{1,-2},{-1,-2}};
queue<p> q;

void bfs(){
    q.push(mp(sx,sy));
    cnt[sx][sy]=1;
    while(!q.empty()){
        p tmp=q.front();q.pop();
        for(int i=0;i<8;++i){
            int xx=tmp.x+f[i][0],yy=tmp.y+f[i][1];
            if(xx<=0||xx>r||yy<=0||yy>c||map[xx][yy]=='*'||cnt[xx][yy])continue;
            cnt[xx][yy]=cnt[tmp.x][tmp.y]+1;
            if(xx==fx&&yy==fy){
                printf("%d",cnt[xx][yy]-1);
                exit(0);//新学的好东西，可以直接结束进程
            }
            q.push(mp(xx,yy));
        }
    }
}

int main(){
    scanf("%d%d",&c,&r);//注意输入
    for(int i=1;i<=r;++i){
        for(int j=1;j<=c;++j){
            scanf(" %c",&map[i][j]);
            if(map[i][j]=='K')sx=i,sy=j;
            if(map[i][j]=='H')fx=i,fy=j;
        }
    }
    bfs();
    return 0;
}

练习:

P1588 [USACO07OPEN]Catch That Cow S

P2199 最后的迷宫

多源 $BFS:$

我们知道，一般的 $BFS$ 都是在同一张图里，对图里的状态做出改变。但有时候，我们需要把整张图作为一个状态，通过这个状态变成另一张图，问最小需要多少步数变成目标状态。也就是说我们要维护的信息由局部变成了整体，这就需要我们的多源 $BFS$。

我们来开启例题 173. 矩阵距离

$Description:$

给定一个 $N$ 行 $M$ 列的 $01$ 矩阵 $A$，$A[i][j]$ 与 $A[k][l]$ 之间的曼哈顿距离定义为：

$$dist(A[i][j],A[k][l])=|i-k|+|j-l|$$

输出一个 $N$ 行 $M$ 列的整数矩阵 $B$，其中：

$$B[i][j]=min_{1≤x≤N,1≤y≤M,A[x][y]=1}dist(A[i][j],A[x][y])$$

简单点说，就是求矩阵中所有位置到离这个位置最近的值为 $1$ 的位置的距离。

$Solution:$

还是利用我们所知的 $BFS$ 的性质：边权相同时，从起点搜起，第一次搜到某个点的路径就是到这个点的单源最短路径。

先来想一下朴素做法：

我们从每个 $1$ 开始做 $BFS$ ，然后每遍历到一个点就保留最小值，这个复杂度显然是会炸掉的（大概是 $O(n^4)$），我们要想想怎么去优化这个做法。

想一想图论里是怎么做的，假如我们要求一个点离它最近的起点的最短距离（注意：这跟多源 $BFS$ 还是有区别的），我们可以把这个问题转化为单源最短路径：我们可以建一个超级源点，这个源点向每一个起点连一条权值为 $0$ 的边，那么从一个点到离它最近的起点的最短路径，就可以转化为从这个点到超级源点的最短路径，所以直接从这个超级源点跑最短路就行了。

那么我们在 $BFS$
里面也可以使用这种思想，只不过我们不需要建超级源点，在这道题里面我们可以把每一个 $1$ 的位置初始化成 $0$ ，再添加到队列里面，然后我们按照普通的最短路模型去跑就行了。

就行了。

为甚么这样是正确的呢？

我们需要证明两个性质：

两段性：就是说，我们最多（因为初始状态都是一样的所以只有一段）可以把 $BFS$ 的队列分成两个有相同值的段，若左边的那一段是 $x$，则右边的一定是 $x+1$。

$Proof:$

从初始状态出发，初始状态都是 $0$ ，则显然我们取出队头遍历之后插回队尾的一定是 $1$。再依此类推，假若我们队头取出的是 $x$ ,则遍历之后插入队尾的一定是 $x+1$。故两段性成立。

单调性：也就是说队列里的值是满足单调性的，由前面的两段性很好推出。

通过这两个性质，我们可以证明出每个结点出队的时候，所存的一定是最短距离。

$Proof:$

首先，初始化的时候显然存的是最短距离。我们可以用反证法：假设之前出队的点最小值已经确定了，那么当前队头元素的最小值也确定了；如果没有确定，那么队列后面必然存在一个元素，它通过遍历可以得到当前队头的这个元素，但又根据单调性，后面的这个元素值一定大于等于前面元素的值，加上每条边权都是 $1$，所以后面这个元素走一圈回到队头这个元素的距离显然一定大于队头元素所存的距离，因此队头元素一定存的是最小值。

所以这个做法是正确的，这样我们也解释了一开始的那个性质为什么成立。

$Code:$

#include<cstdio>
#include<queue>
using namespace std;

const int N=1010;
typedef pair<int,int> p;
#define mp(x,y) make_pair(x,y)
#define x first
#define y second

int n,m;
int g[N][N],dist[N][N];
int f[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
bool vis[N][N];
queue<p> q;

void bfs(){
    while(!q.empty()){
        p tmp=q.front();q.pop();
        for(int i=0;i<4;++i){
            int xx=tmp.x+f[i][0],yy=tmp.y+f[i][1];
            if(xx<=0||xx>n||yy<=0||yy>m||vis[xx][yy])continue;
            dist[xx][yy]=dist[tmp.x][tmp.y]+1;
            vis[xx][yy]=true;
            q.emplace(mp(xx,yy));
        }
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            scanf("%1d",&g[i][j]);
            if(g[i][j]){
                q.emplace(mp(i,j));//又是个新东西，等价于push
                vis[i][j]=true;
            }
        }
    }
    bfs();
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            printf("%d ",dist[i][j]);
        }
        puts("");
    }
    return 0;
}

双端队列 $BFS:$

有的时候，我们要维护最小值，不一定要从队尾插入，也可以从队头插入以更好地求解答案，所以我们需要拿一个双端队列来维护 $BFS$。

例题：P4667 [BalticOI 2011 Day1]Switch the Lamp On

$Description:$

有一种正方形的电路元件，在它的两组相对顶点中，有一组会用导线连接起来，另一组则不会。有 $N\times M$ 个这样的元件，你想将其排列成 $N$ 行，每行 $M$ 个。电源连接到板的左上角。灯连接到板的右下角。只有在电源和灯之间有一条电线连接的情况下，灯才会亮着。为了打开灯，任何数量的电路元件都可以转动 $90\degree$（两个方向）。

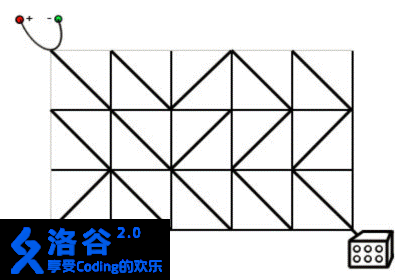
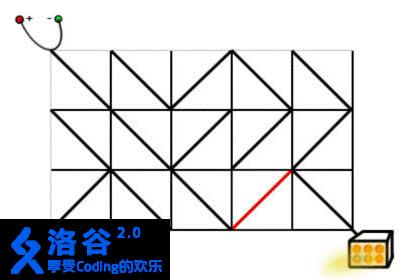
在上面的图片中，灯是关着的。如果右边的第二列的任何一个电路元件被旋转 $90\degree$，电源和灯都会连接，灯被打开。现在请你编写一个程序，求出最小需要多少旋转多少电路元件。

$Solution:$

这道题可以理解成从左上走到右下的最短路问题，如果可以直接走的话边权就为 $0$，如果要旋转后才能走的话边权就为 $1$。也就是说，我们要在这样一个边权只有 $0$ 或 $1$ 两种情况的无向图中走最短路。

先来看看无解的情况吧，我们来看下面这张图：

上面圈红色的点是无论如何都到不了的，我们可以从中找一下性质，我们可以发现，到不了的点其横纵坐标和都为奇数，到的了的点和都为偶数，所以可以靠这个性质判断是否有解。

我们前面说到的 $BFS$ 的性质是在边权都一样的情况的，然而这道题边权有两种，我们该怎么处理呢？（当然这道题用 $Dijkstra$ 是可以过的）

这就需要我们的双端队列 $BFS$ 了，在 $BFS$ 的队列里面，我们要保证单调性，使得每一次从队头取出来的元素都是当前最小的，所以我们每次取出元素遍历时，遇到权值为 $0$ 的边，就把他放到队首，反之则放到队末，这样就可以保证单调性了，也说明这个做法是正确的（可以参考上面多源 $BFS$ 的单调性证明）。其余部分都与一般的 $BFS$ 是一样的。

$Code:$

#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

const int N = 501;
typedef pair<int,int> p;
#define x first
#define y second

int n,m,dis[N][N];
int f1[4][2]={{-1,-1},{-1,1},{1,-1},{1,1}};//点与点的坐标关系：左上、右上、左下、右下
int f2[4][2]={{-1,-1},{-1,0},{0,-1},{0,0}};//点与边的坐标关系：左上、右上、左下、右下
char g[N][N],edge[5]="\\//\\";//四个方向的边能顺着走的样子（多打一个‘\’是转义）
bool vis[N][N];

int bfs(){
    deque<p>q;
    memset(vis,0,sizeof vis);
    memset(dis,0x3f,sizeof dis);
    dis[0][0]=0;//注意点从(0,0)开始
    q.push_back({0,0});
    while(!q.empty()){
        p tmp=q.front();q.pop_front();
        if(tmp.x==n&&tmp.y==m)return dis[n][m];
        if(vis[tmp.x][tmp.y])continue;
        vis[tmp.x][tmp.y]=true;
        for(int i=0;i<4;++i){
            int px=tmp.x+f1[i][0],py=tmp.y+f1[i][1];//点坐标
            if(px<0||px>n||py<0||py>m)continue;
            int ex=tmp.x+f2[i][0],ey=tmp.y+f2[i][1];//边坐标
            int w=(g[ex][ey]!=edge[i]);//获得边权：需不需要旋转
            int dist=dis[tmp.x][tmp.y]+w;
            if(dist<dis[px][py]){//更新
                dis[px][py]=dist;
                if(!w)q.push_front({px,py});
                else q.push_back({px,py});
            }
        }
    }
    return 0;
}

int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;++i){
            for(int j=0;j<m;++j){
                scanf(" %c",&g[i][j]);
            }
        }
        if((n+m)&1){
            puts("NO SOLUTION");
            continue;
        }
        printf("%d\n",bfs());
    }
    return 0;
}

最小步数模型：

顾名思义，就是用来求解通过一种或几种方式，从一个状态到目标状态的最小步数，这里来看一下例题 P2730 [USACO3.2]魔板 Magic Squares

$Description:$

这是一张有 $8$ 个大小相同的格子的魔板：

1 2 3 4
8 7 6 5

我们知道魔板的每一个方格都有一种颜色。

这 $8$ 种颜色用前 $8$ 个正整数来表示。

可以用颜色的序列来表示一种魔板状态，规定从魔板的左上角开始，沿顺时针方向依次取出整数，构成一个颜色序列。

对于上图的魔板状态，我们用序列 $(1,2,3,4,5,6,7,8)$ 来表示，这是基本状态。

这里提供三种基本操作，分别用大写字母 $A$，$B$，$C$ 来表示（可以通过这些操作改变魔板的状态）：

A：交换上下两行；

B：将最右边的一列插入到最左边；

C：魔板中央对的4个数作顺时针旋转。

下面是对基本状态进行操作的示范：

对于每种可能的状态，这三种基本操作都可以使用。

你要编程计算用最少的基本操作完成基本状态到特殊状态的转换，输出基本操作序列。

$Solution:$

这类的题往往有一些特点，那就是状态的存储，一般来说，我们状态可以用哈希表来存储。在这个问题里，我们用哈希表来存每个状态是否出现过，如果没出现过就记录下这个方案。除此之外我们还要记录当前状态是由哪个状态得来的，这个相比于前面的迷宫问题比较特殊，必须从起点开始推，所以最后记录一下答案然后 $reverse$ 一下就行。

$Code:$

#include<unordered_map>//注意考场上不能用
#include<queue>
#include <iostream>
#include <cstring>
#include <algorithm>
#include<cstdio>
using namespace std;

string st,ed;
unordered_map<string,int>dist;
unordered_map<string,pair<char,string>>pre;
queue<string>q;


//对应三个操作
string A(string now){
    for(int i=0;i<=3;++i)swap(now[i],now[7-i]);
    return now;
}//1 2 3 4 5 6 7 8->8 7 6 5 4 3 2 1

string B(string now){
    string res=now;int k=0;
    res[0]=now[3];res[7]=now[4];
    for(int i=0;i<3;++i)res[++k]=now[i];
    for(int i=5;i<8;++i)res[++k]=now[i];
    return res;
}//1 2 3 4 5 6 7 8->4 1 2 3 6 7 8 5

string C(string now){
    string res=now;
    res[1]=now[6];res[2]=now[1];res[5]=now[2];res[6]=now[5];
    return res;
}//1 2 3 4 5 6 7 8->1 7 2 4 5 3 6 8


void bfs(){
    q.push(st);
    while(!q.empty()){
        string tmp=q.front();q.pop();
        //提前预处理
        string state[3];
        state[0]=A(tmp);
        state[1]=B(tmp);
        state[2]=C(tmp);

        for(int i=0;i<3;++i){
            if(!dist.count(state[i])){
                dist[state[i]]=dist[tmp]+1;
                pre[state[i]]={(char)(i+'A'),tmp};
                if(state[i]==ed){
                    return;
                }
                q.push(state[i]);
            }
        }
    }
}

int main(){
    //预处理起始和终点状态
    for(int i=1;i<=8;i++){
        int x;scanf("%d",&x);
        ed+=(char)(x+'0');
    }
    for(int i=1;i<=8;++i)st+=(char)(i+'0');

    bfs();
    printf("%d\n",dist[ed]);

    string res;
    while(ed!=st){
        res+=pre[ed].first;
        ed=pre[ed].second;
    }

    reverse(res.begin(),res.end());//逆序
    cout<<res;

    return 0;
}

先咕到这里

0 评论

App 内打开

搜索算法学习笔记

此笔记始于 $2021.4.3$，蒟蒻在 $AcWing$ 学习搜索算法 （QAQ没有打广告啊）

$BFS$ 特点

$Flood\ Fill$ 模型

模型介绍：

$Description$：

$Solution:$

$Code:$

$Description$：

$Solution:$

$Code:$

练习：

最短路模型

模型介绍

$Description:$

$Solution:$

$Code:$

$Description:$

$Solution:$

$Code:$

练习:

多源 $BFS:$

$Description:$

$Solution:$

$Proof:$

$Proof:$

$Code:$

双端队列 $BFS:$

$Description:$

$Solution:$

$Code:$

最小步数模型：

$Description:$

$Solution:$

$Code:$

0 评论

此笔记始于 $2021.4.3$，蒟蒻在 $AcWing$ 学习搜索算法（QAQ没有打广告啊）