浅谈 SPT

本篇文章参考 这篇日报

介绍

SPT，即 Shortest Path Tree，最短路径树。

如下图，我们假设源点为 1，

则由它生成的 SPT 为：

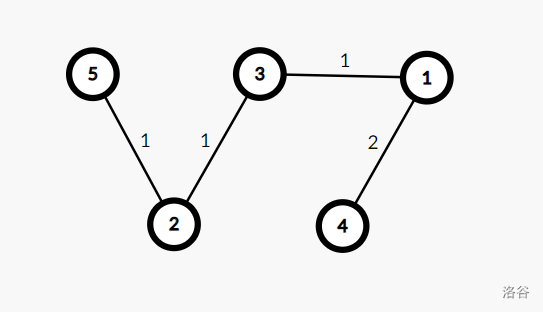
从中我们可以发现 SPT 要满足的一些性质：

• 是一颗生成树，每个点连通。
• 从根节点到树上任意一点的距离即为原图中源点到该点的最短路。

我们如何构造 SPT 呢？

我们可以用 Dijkstra、Floyd 等算法，这里我们只说用 Dijkstra 的做法。

我们记录一个数组 $pre$，$pre_i$ 表示从源点到点 $i$ 的最短路径上与 $i$ 相连的边的编号，即 $i$ 的上一条边，每次松弛时更新。

//这是松弛的代码
for(int i=h[u];i;i=ne[i]){
    int v=e[i];
    if(dis[v]>=dis[u]+w[i]){
        dis[v]=dis[u]+w[i];
        q.push((node){v,dis[v]});
        pre[v]=i;
    }
}

这里我来解释一下为什么代码中 $dis_v>=dis_u+w_i$。首先 $dis_v>dis_u+w_i$ 时显然是要更新的；当 $dis_v=dis_u+w_i$ 时，如图：

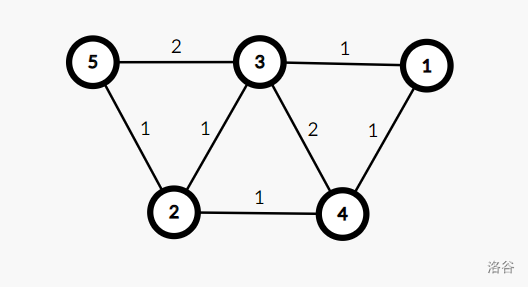
对于 $1$ 到 $5$，我们有两个路径：

1. 1->3->5

2. 1->3->2->5

它们的长度都是 $3$。但是我们来看一下两种路径下的生成树：

这是第一种：

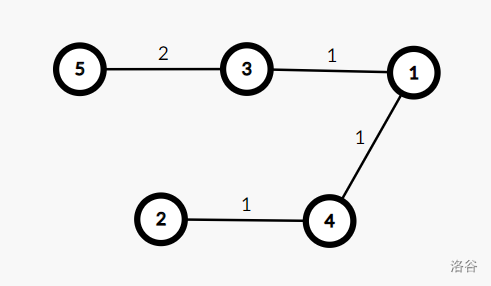
这是第二种：

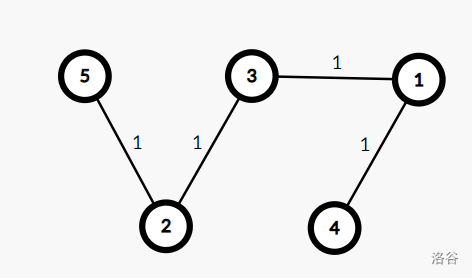
第一种的权值和为 $5$，第二种的权值和为 $4$，显然第二种才是我们要求的 SPT。从中我们可以看出，我们要使任意两点相连的边的边权尽可能小。

那为什么直接加个等于号就行了呢？这篇博客讲的很好。

还是以原图为例：

我们要扩展到 $5$，首先会扩展到 $2$ 和 $3$。由于 $dis_2 < dis_3$，根据 Dijkstra 的性质，会先扩展 $dis$ 最小的那一个，所以 $3$ 会先被扩展到。由于源点经过 $2$ 和 $3$ 到 $5$ 的路径长度相等，又 $dis_2 > dis_3$，所以 $edge_{2,5}<edge_{3,5}$。因为 $2$ 是后扩展到的，所以直接覆盖就行了。如果还有点满足这种关系也同理。

再来说说输出解。SPT 是一颗树，也就是说，从根到某一结点只有一条简单路径，只有 $n-1$ 条边。那么除根结点外，每一个结点都对应一条边，也就是它们的 $pre$。由于加的是双向边，输出的时候应为 $(pre_i+1)/2$。

tips: 不开 long long 见祖宗qwq

$Code:$

#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;

const int N=3e5+10,M=N<<1,inf=0x7f;

int n,m,s;
int h[N],e[M],ne[M],w[M],idx;
int pre[N];
long long dis[N];
bool vis[N];
struct node{
    int to;long long w;
    inline bool operator <(const node& a)const{
        return w>a.w;
    }
};
priority_queue<node>q;

inline void add(int a,int b,int c){
    e[++idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx;
}

void dij(){
    memset(dis,inf,sizeof dis);
    q.push((node){s,0});dis[s]=0;
    while(!q.empty()){
        int u=q.top().to;q.pop();
        if(vis[u])continue;
        vis[u]=true;
        for(int i=h[u];i;i=ne[i]){
            int v=e[i];
            if(dis[v]>=dis[u]+w[i]){
                dis[v]=dis[u]+w[i];
                q.push((node){v,dis[v]});
                pre[v]=i;
            }
        }
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i){
        int a,b,c;scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);add(b,a,c);
    }
    scanf("%d",&s);
    dij();
    long long sum=0;
    for(int i=1;i<=n;++i){
        if(i==s)continue;
        sum+=w[pre[i]];
    }
    printf("%lld\n",sum);
    for(int i=1;i<=n;++i)if(i!=s)printf("%d ",pre[i]+1>>1);
    return 0;
}