0.前言

最近学了一点基础的质数筛，之前一直都写的是暴力，现在打算写篇博客稍微介绍一下这些筛法。

如有错误，请各位读者不要吝惜您的宝贵建议，请一定向作者指出！也欢迎提供给作者更高级的筛法，我会找时间了解并将其写进这篇博客，谢谢各位的指导！

1.正片

朴素算法应该大家都会了，就是前言中的暴力，即试除法，枚举因数，看看被筛数是否能除得尽，是的话是合数，否则是素数。

代码如下

for(int i=2;i<=n;i++)
{
    bool f=true;
    for(int j=2;j*j<=i;j++) if(i%j == 0) {f=false; break;}
    if(f) printf("%d ",i);
}   

一个优化：枚举范围从2（因为所有正整数数都是1的倍数）到$\sqrt{n}$即可（因为如果油比$\sqrt{n}$更大的因数，那该因数一定能和之前一个比$\sqrt{n}$小的n的因数配对）。

但窝们不难发现，这种筛法是有缺陷的：对每一个数都必须从2到$\sqrt{n}$枚举，对于范围较大的题目，很有可能超时。

介绍一种较快的筛法：埃氏筛法

埃氏筛法：对于每一个合数，一定存在一个m|n,其中m是n的最小素因子。利用这一特性，对每一个素数，枚举ta的倍数，将ta们都标记成合数，之后不再理会。

代码如下

int n=100,prime[110];
for(int i=2;i<=n;i++)
    if(!prime[i])
    {
        printf("%d ",i);
        for(int j=i*i;j<=n;j+=i) prime[j]=1;
    }

一个优化：枚举范围从i$\times$i（因为2~i-1在2~i-1时已经被筛去）到
n即可。

但埃筛依然有缺陷：一个合数，比如6，会被几个不同的质数（2，3）重复标记，使我们的效率下降。

时间上更优的是欧拉筛。（欧拉怎么啥都会

欧拉筛：对于每一个合数，只用ta的最小素因子去筛，用一个数组记录素数以避免重复。

代码如下

不要吐槽我的变量名，我随便起的

for(int i=2;i<=n;i++)
{
    if(!prime[i]) {vis[++cnt]=i; printf("%d ",i);}
    for(int j=1;j<=cnt && vis[j]*i<=n;j++)
    {
        int t=vis[j];
        prime[t*i]=1;
        if(i%t == 0) break;
    }
}

实现过程：对于每一个当前数，枚举之前找到的质数，枚举当前数的素数倍，标记为合数。这样保证了每个数只被ta最小的素因子筛一次（因为大的素数会比小的素数慢找到）。

2.结束语

一次偶然的机会，窝接触了上述两种优化的算法，其实这些比较基础，但窝接触得很晚，于是想写篇博客记录下来希望煤油错误。

卡埃筛的题不多，您基本可以放心写，不过具体还是要视题目而言（万一是道毒瘤题呢）。

几道题目（dalao们肯定不屑一顾/kk）

• 模板题1

• 模板题2

• 模版题3

• 灵活运用：一道省选橙题

这篇博客就是这样了，祝大家阅读愉快，早日

$\color{black}AK IOI!$

3.update

2.27更新区间筛

模板-P1835 素数密度

摘自Krydom课件

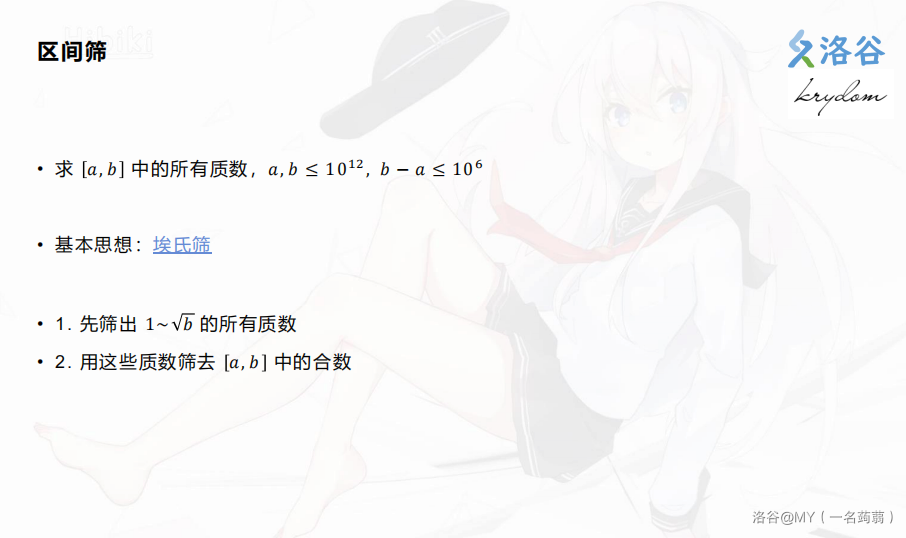
具体实现：第一步欧拉筛将质数存到数组里面，第二步注意下埃筛的倍数枚举最小从2开始。

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N=1e6+10;

long long l,r;
int p[N],tot,ans;
bool vis[N];

int main()
{
//  freopen("work.in","r",stdin); freopen("work.out","w",stdout);
    scanf("%lld%lld",&l,&r);
    int n=sqrt(r);
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]) p[++tot]=i;
        for(int j=1;j<=tot && p[j]*i<=n;j++)
        {
            vis[p[j]*i]=true;
            if(i%p[j] == 0) break;
        }
    }
    for(int i=0;i<=n;i++) vis[i]=false;
    for(int i=1,x;i<=tot;i++)
    {
        x=l/p[i]; if(x < 2) x=2;//所谓细节
        for(int j=x;j<=r/p[i];j++)
            if(j*p[i]-l >= 0) vis[j*p[i]-l]=true;
    }
    for(int i=0;i<=r-l;i++) if(!vis[i]) ans++;
    printf("%d",ans);
//  fclose(stdin); fclose(stdout);
    return 0;
}

练习

• UVA10140 Prime Distance