智障my手贱删了还是个宝宝的第一版。
学习资料
在笔记中主要对OI Wiki中的内容进行补充。
差分约束用来解决 $n$ 元一次不等式组的求解问题。
为啥可以转化成三角形不等式在图上跑
注意到每一个不等式都是形如 $x_{c_i}\ -\ x_{c^{\prime}_i}\ \le\ y_i$ 的形式。
移项得 $x_{c_i}\ \le\ y_i\ +\ x_{c^{\prime}_i}$ 。
注意到这个不等式是具有传递性的。也就是说, $x_{c^{\prime}_i}$ 也可以表示成类似 $x_{c^{\prime}_i}\ \le\ y_k\ +\ x_{c_k}$ 的形式。
由于题目中一般都会有对差分约束解集的限制,所以最终对于每一个 $x_i$ ,都满足
$$x_i\ \le\ x_j\ +\ k_j \ \le\ x_{j_1}\ +\ k_j\ + \ k_{j_1}\ \le \ …\ \le\ x_0\ +\ k_{1\ldots n}$$
其中 $x_0$ 是超级源点的点权,也就是题目给的常数, $k$ 是不等式中的常数。
对应到图上,一条不等式链对应的就是一个联通图中源点到图上任意一个点的路径。
那么因为不等式链具有传递性,如果图中这样的关系形成了环,那么这个差分约束系统无解。
于是我们要建立超级源点,确保图联通,我们才能从超级源点到达每一个点。
模板的代码
#include <cstdio>
#include <iostream>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <queue>
using namespace std;
const int N=5e3+10;
int n,m,tot,fir[N],dis[N],cnt[N];
bool in[N];
struct edge {int to,nex,w;} e[N << 1];//有超级源点
queue <int> q;
inline void add(int u,int v,int w)
{
e[++tot].to=v; e[tot].nex=fir[u];
e[tot].w=w; fir[u]=tot; return ;
}
bool spfa(int u)
{
int v;
q.push(u);
dis[0]=0; in[0]=true;
while(!q.empty())
{
u=q.front(); q.pop();
in[u]=false;
for(int i=fir[u];i;i=e[i].nex)
if(dis[v=e[i].to] > dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
cnt[v]=cnt[u]+1;
if(cnt[v] > n) return false;//加了一个点
if(!in[v]) {q.push(v); in[v]=true;}
}
}
return true;
}
int main()
{
// freopen("work.in","r",stdscanfin); freopen("work.out","w",stdout);
scanf("%d%d",&n,&m);
int u,v,w;
while(m--)
{
scanf("%d%d%d",&u,&v,&w);
add(v,u,w);
}
for(int i=1;i<=n;i++) {dis[i]=1e9; add(0,i,0);}
if(spfa(0)) for(int i=1;i<=n;i++) printf("%d ",dis[i]);
else printf("NO");
// fclose(stdin); fclose(stdout);
return 0;
}
优化:spfa判负环时建立一个 $cnt$ 数组记录从源点到每一个点的最短路上一共包含多少条边,当边数大于等于 $n$ 是则存在负环。当然可以使用记录每一个点入队次数的方法,不过这种方法一般不如以上方法快。在有需要的情况下,我们也可以同时使用这两种方法。
算法没有本质不同,这里给出核心的转化部分。
if(op == 1) add(u,v,-w);
if(op == 2) add(v,u,w);
if(op == 3) {add(u,v,0); add(v,u,0);}//相等两者必须同时满足
我打最短路为啥挂了
这题打最短路然后加上最小值并不会挂,但如果要求所有 $x_i$ 的最小值,那么直接这样做就是错的。
先来讲一下啥时候打最短路是正确的。
我们刚才讲过,一条不等式链对应的就是一个联通图中源点到图上任意一个点的路径。
这样的路径显然不止一条。
对于每一个 $x_i$ ,可能有 $x_i$ 满足
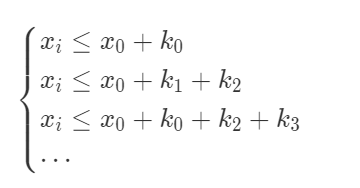
以上为举例,其中 $k$ 为边权。
那么 $x_i$ 的最大值是所有不等式右边的最小值。
也就是说,跑最短路时,我们求的是解的最大值。
同理求最小值时,不等号方向改变,我们要跑最长路。
下面这题就是典型的求最小值,跑最长路。
这题正解是tarjan+DP,但是我们想用差分约束来解决。
关于此题的几个卡常:
1. 当 $2$ 和 $4$ 操作的两个点相同时,直接判断无解
2. 建超级源点时反序建边
3. 双端队列优化
其中后面两个优化我不是很懂。希望有人能给蒟蒻解释一下。
#include <cstdio>
#include <iostream>
#include <deque>
using namespace std;
const int N=1e5+10;
int n,m,fir[N],tot,dis[N],cnt[N];
bool in[N];
struct edge {int to,nex,w;} e[N << 2];
inline void add(int u,int v,int w)
{
e[++tot].w=w; e[tot].to=v;
e[tot].nex=fir[u]; fir[u]=tot; return ;
}
bool spfa(int u)
{
deque <int> q;
int v; q.push_back(0);
while(!q.empty())
{
u=q.front(); q.pop_front(); in[u]=false;
for(int i=fir[u];i;i=e[i].nex)
if(dis[v=e[i].to] < dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
cnt[v]=cnt[u]+1;
if(cnt[v] == n+1) return false;
if(!in[v])
{
in[v]=true;
if(dis[v] > dis[q.front()]) q.push_front(v);
else q.push_back(v);
}
}
}
return true;
}
int main()
{
// freopen("work.in","r",stdin); freopen("work.out","w",stdout);
scanf("%d%d",&n,&m);
int op,u,v;
while(m--)
{
scanf("%d%d%d",&op,&u,&v);
if(u == v && (op == 2 || op == 4)) return printf("-1"),0;
if(op == 1) {add(u,v,0); add(v,u,0);}
if(op == 2) add(u,v,1);//最长路
if(op == 3) add(v,u,0);
if(op == 4) add(v,u,1);
if(op == 5) add(u,v,0);
}
for(int i=n;i>0;i--) {add(0,i,1); dis[i]=-1e9;}//最少每人一个
if(spfa(0))
{
long long ans=0;
for(int i=1;i<=n;i++) ans+=dis[i];
printf("%lld",ans);
}
else printf("-1");
// fclose(stdin); fclose(stdout);
return 0;
}
习题
需要思路可以私信作者或在评论区提出建议。

