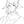弗洛伊德算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题,同时也被用于计算有向图的传递闭包。
适用范围:无负权回路即可,边权可正可负,运行一次算法即可求得任意两点间最短路。
思路
Floyd算法:求出每⼀对顶点之间的最短路径使⽤动态规划思想,将问题的求解分为多个阶段对于n个顶点的图G,求任意⼀对顶点Vi —> Vj之间的最短路径可分为如下⼏个阶段:
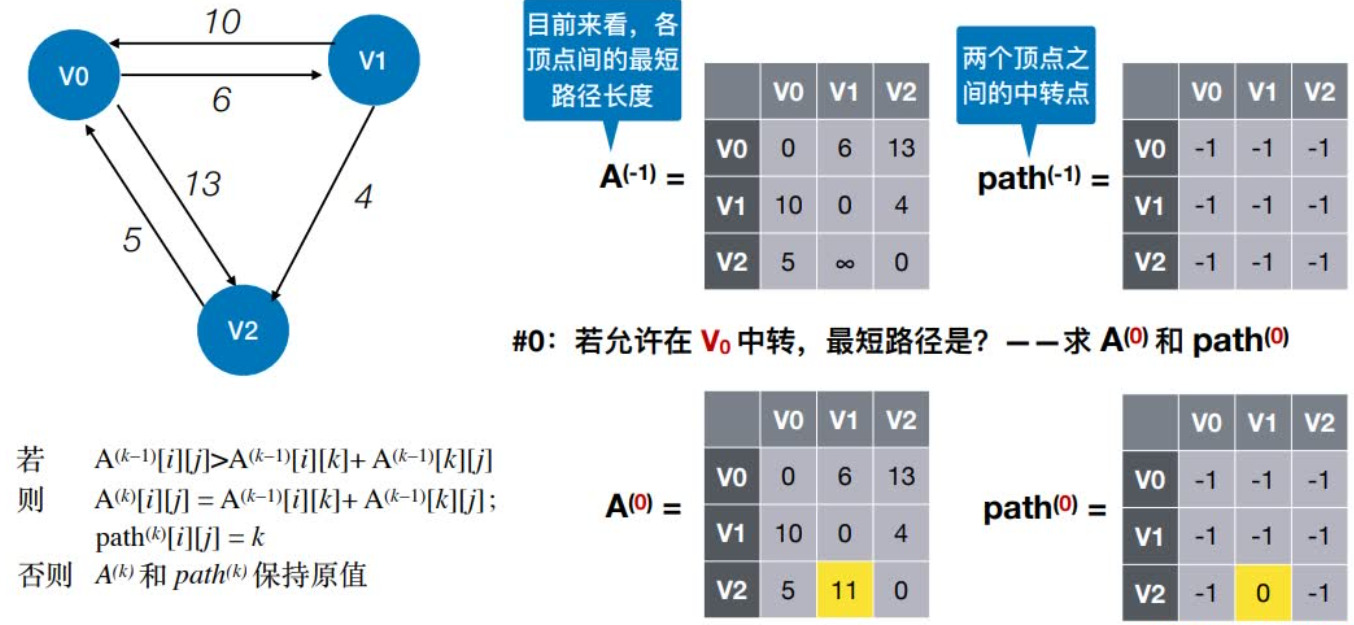
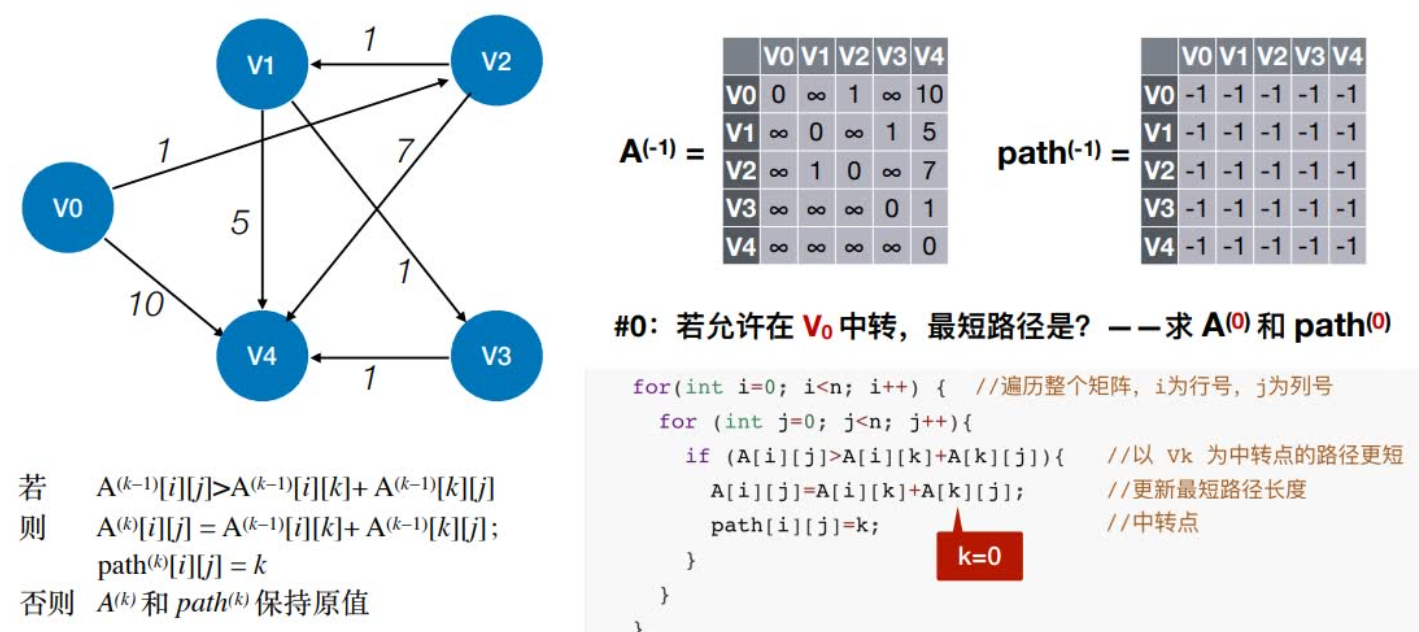
初始:不允许在其他顶点中转,最短路径是?
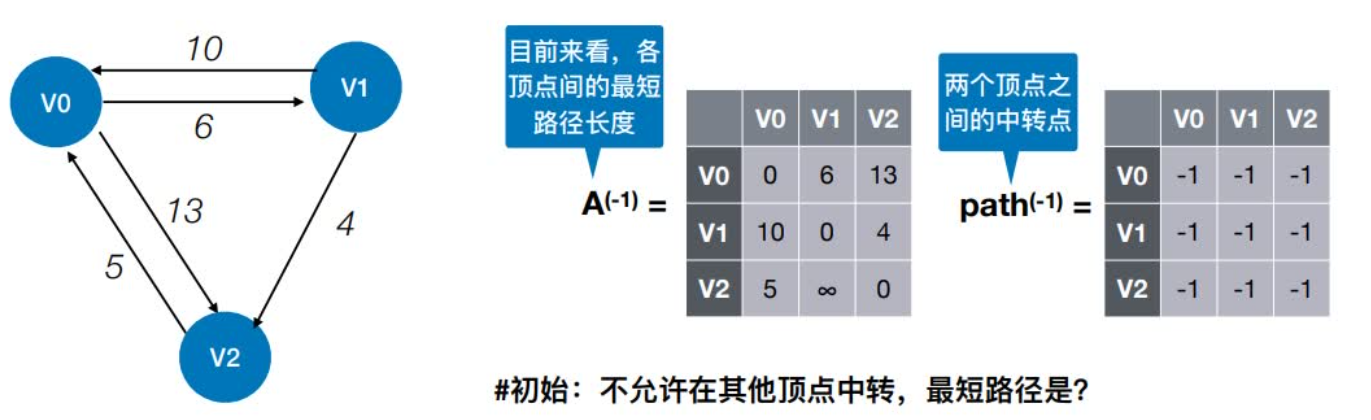
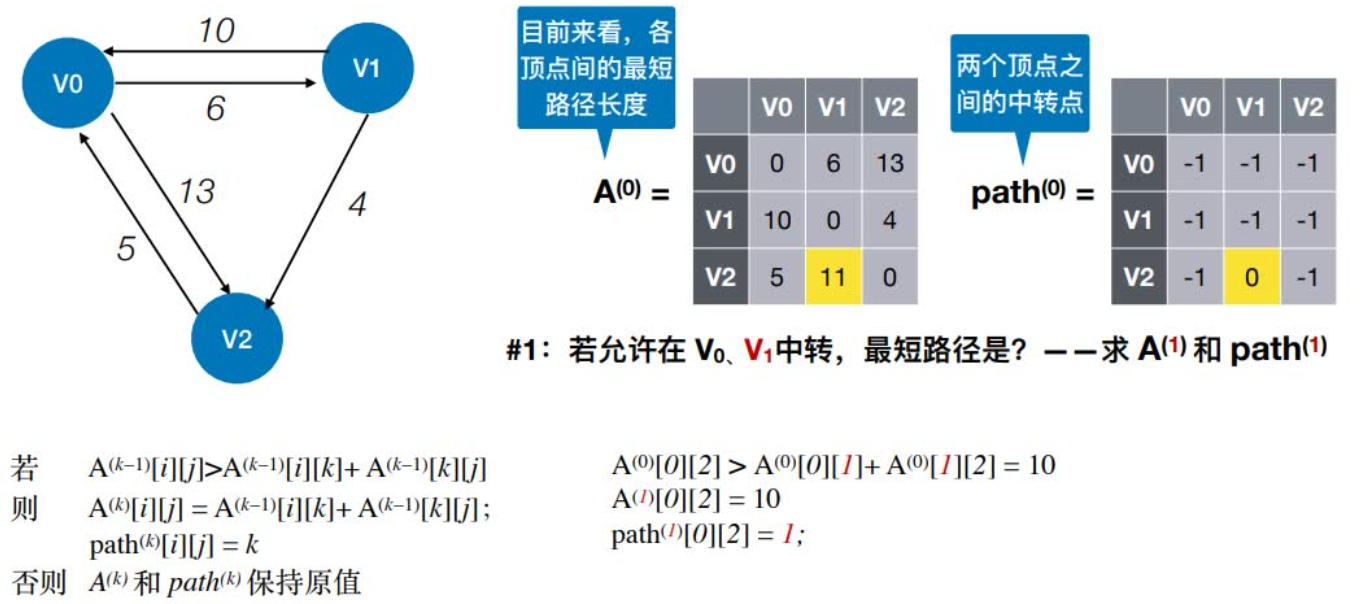
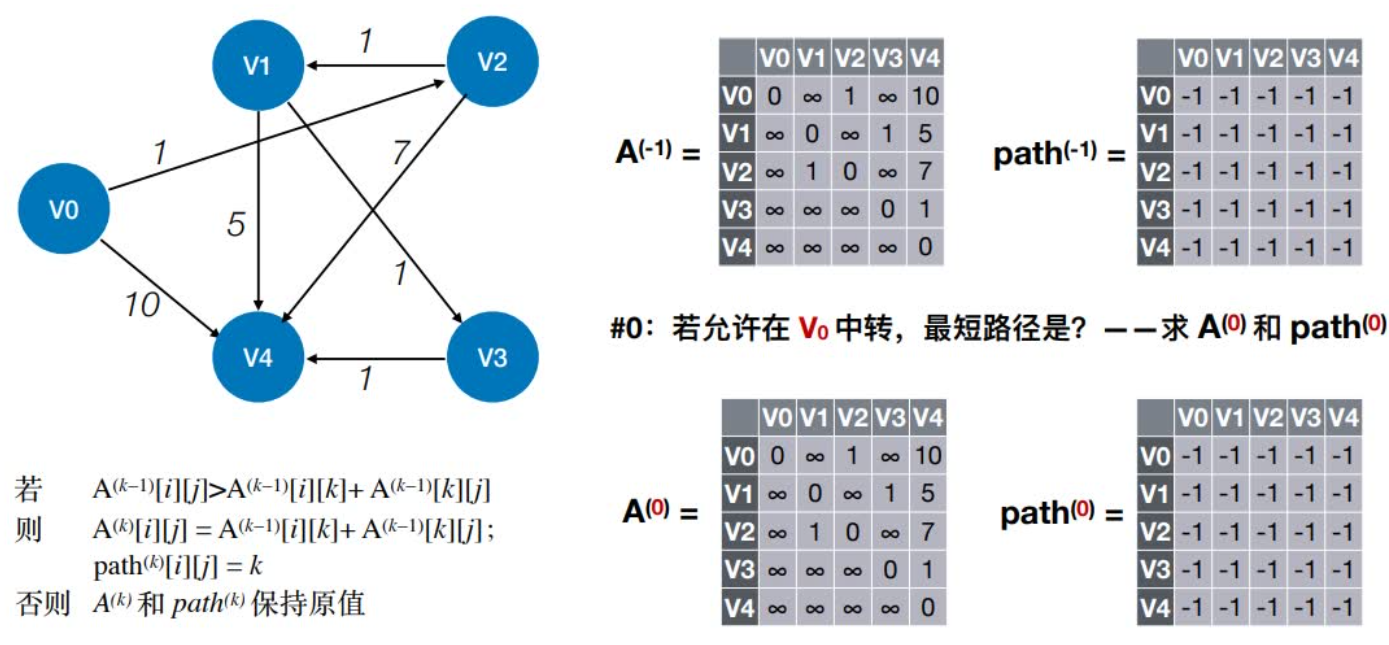
0:若允许在V0中转,最短路径是?
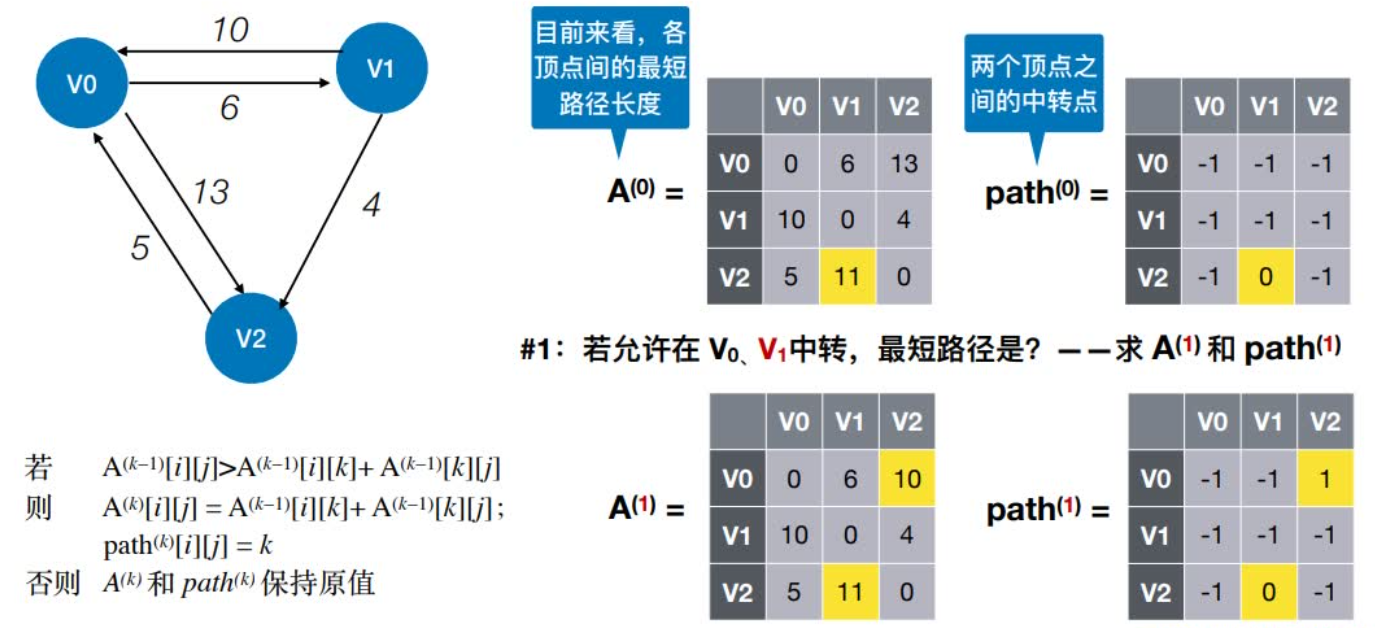
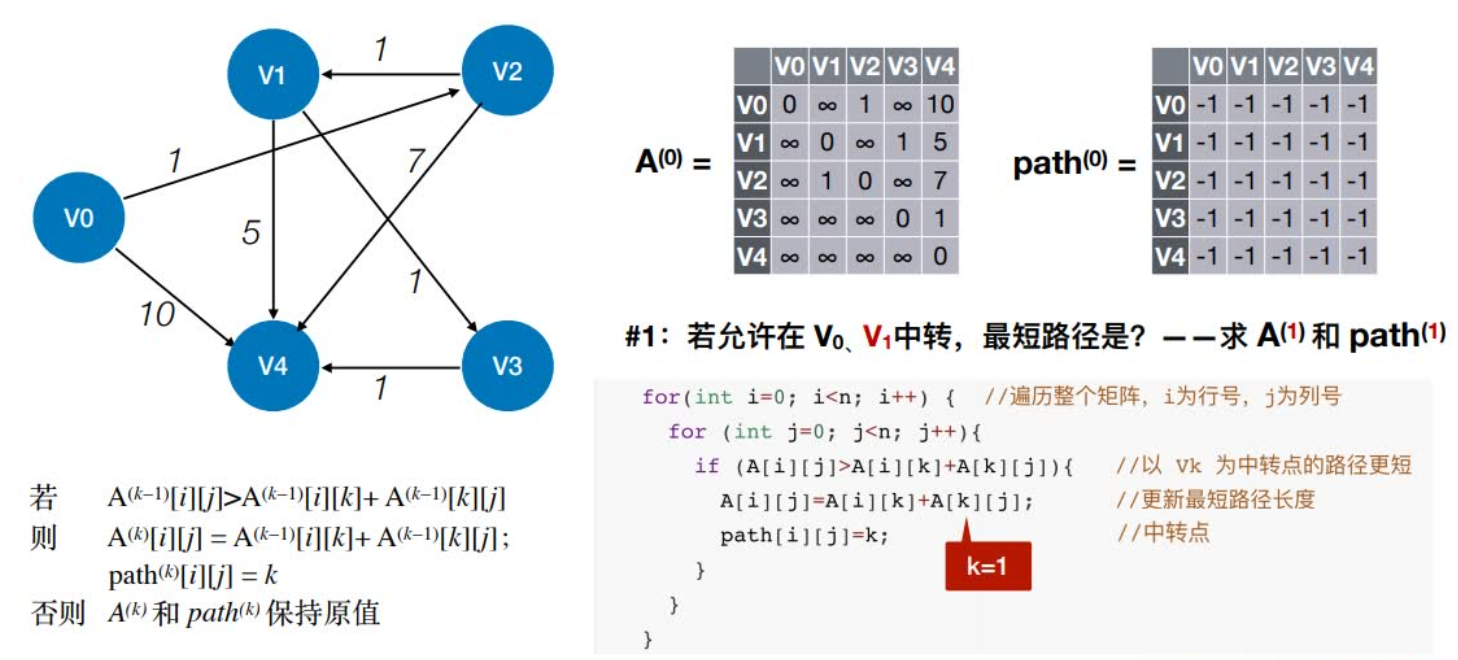
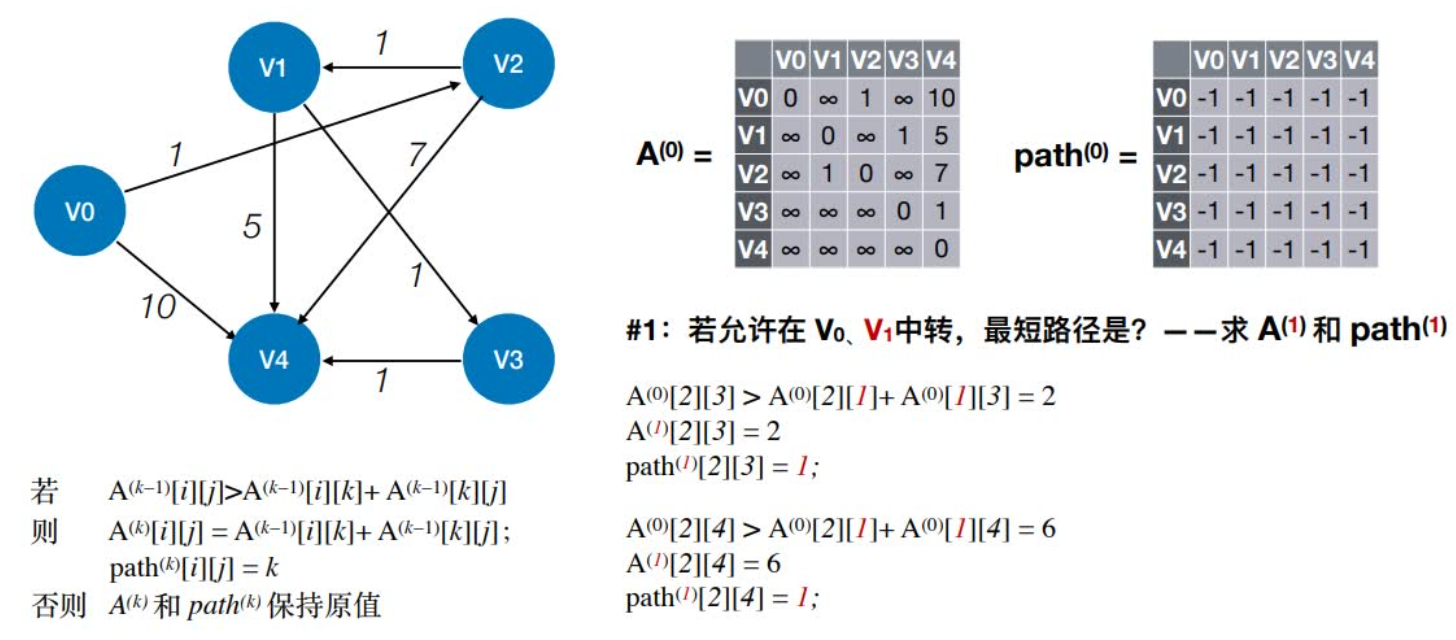
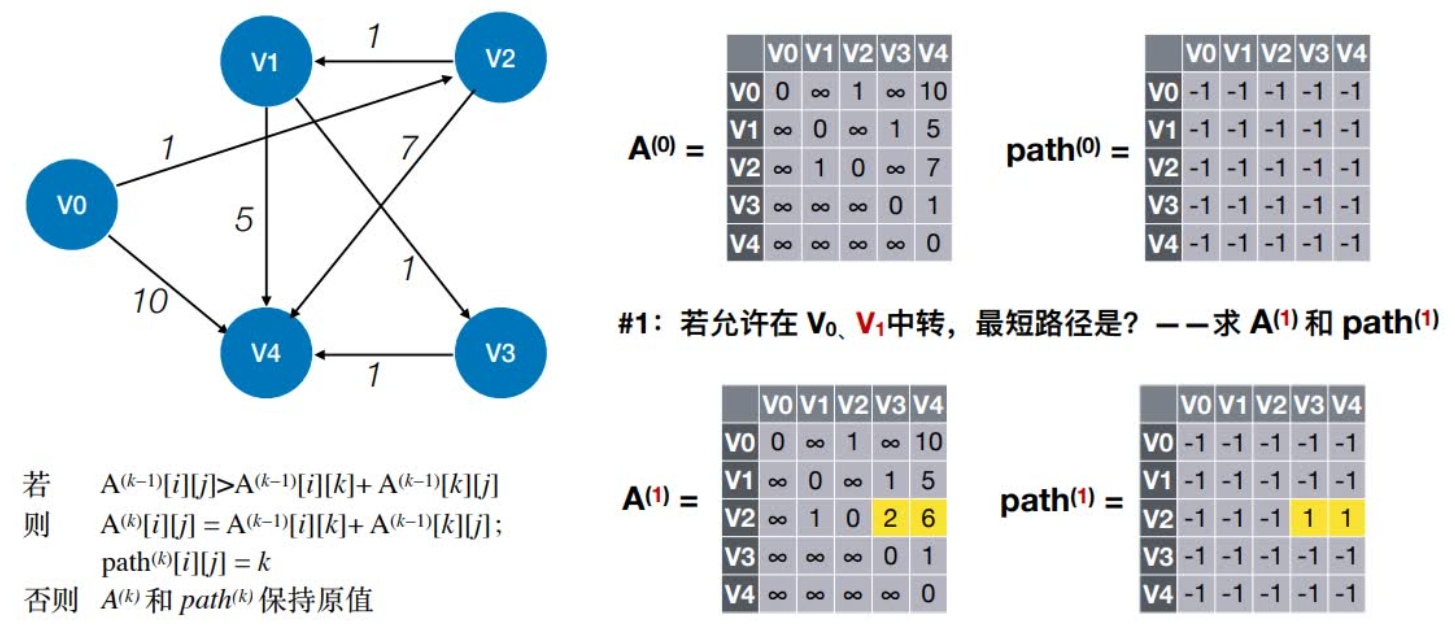
1:若允许在V0、V1中转,最短路径是?
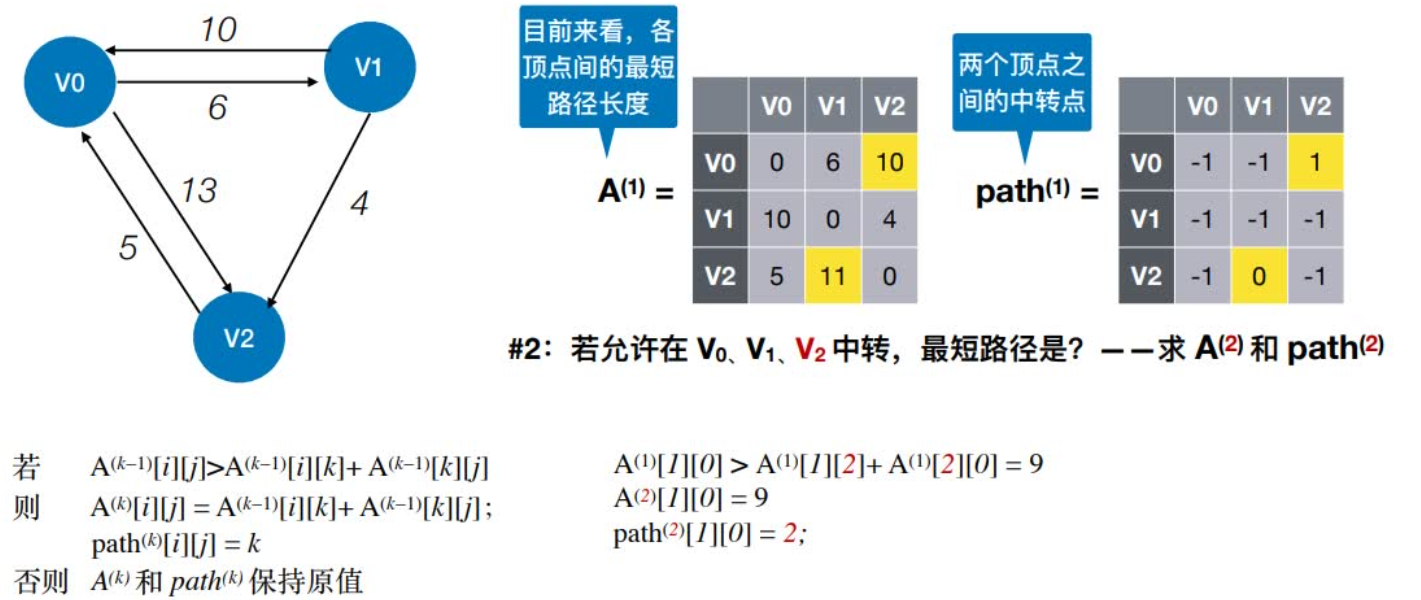
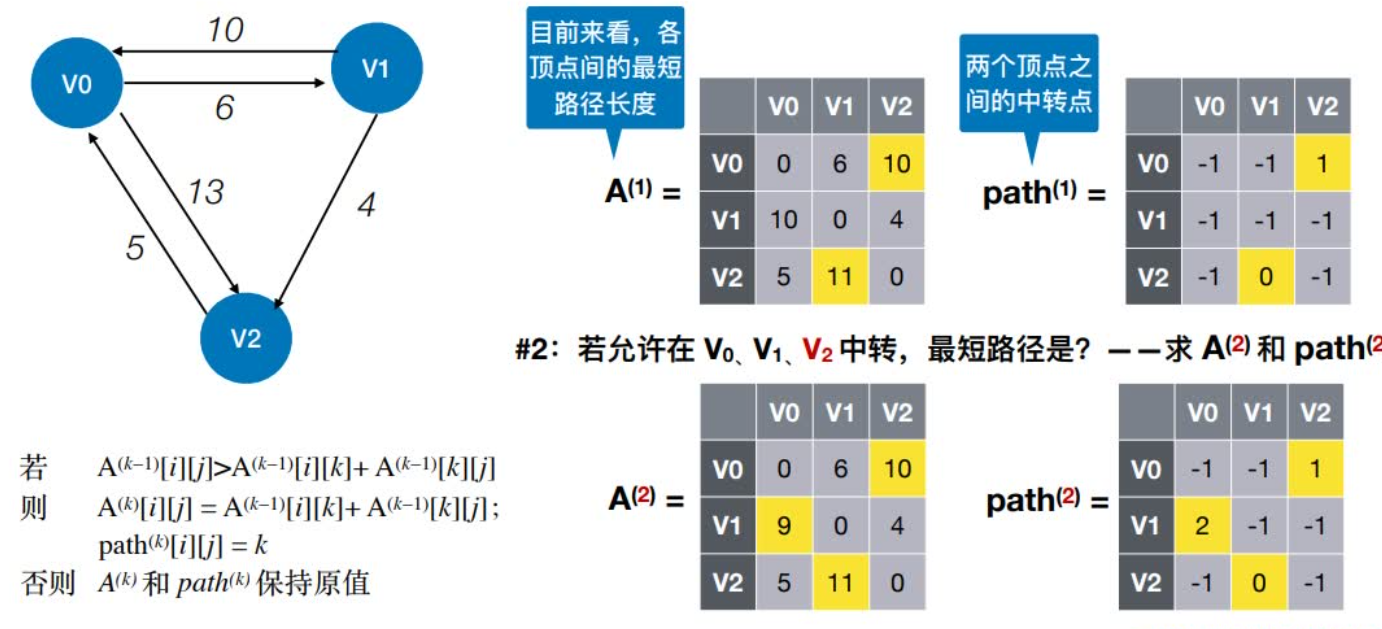
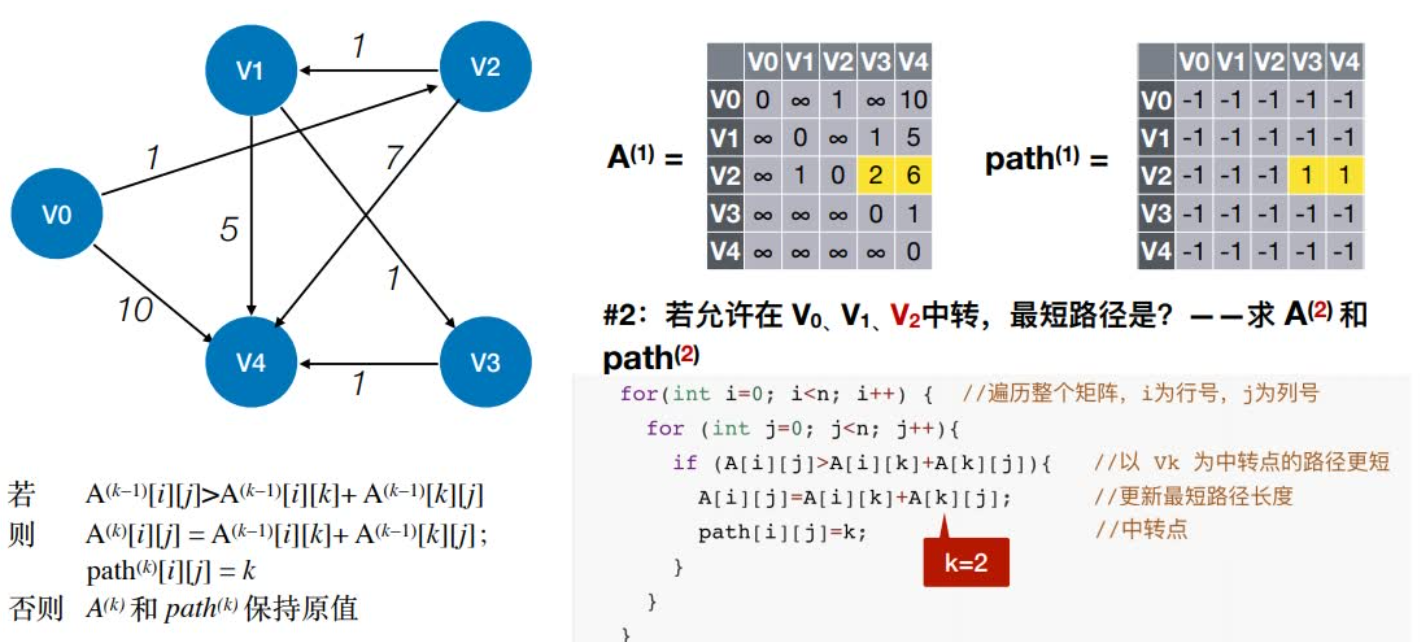
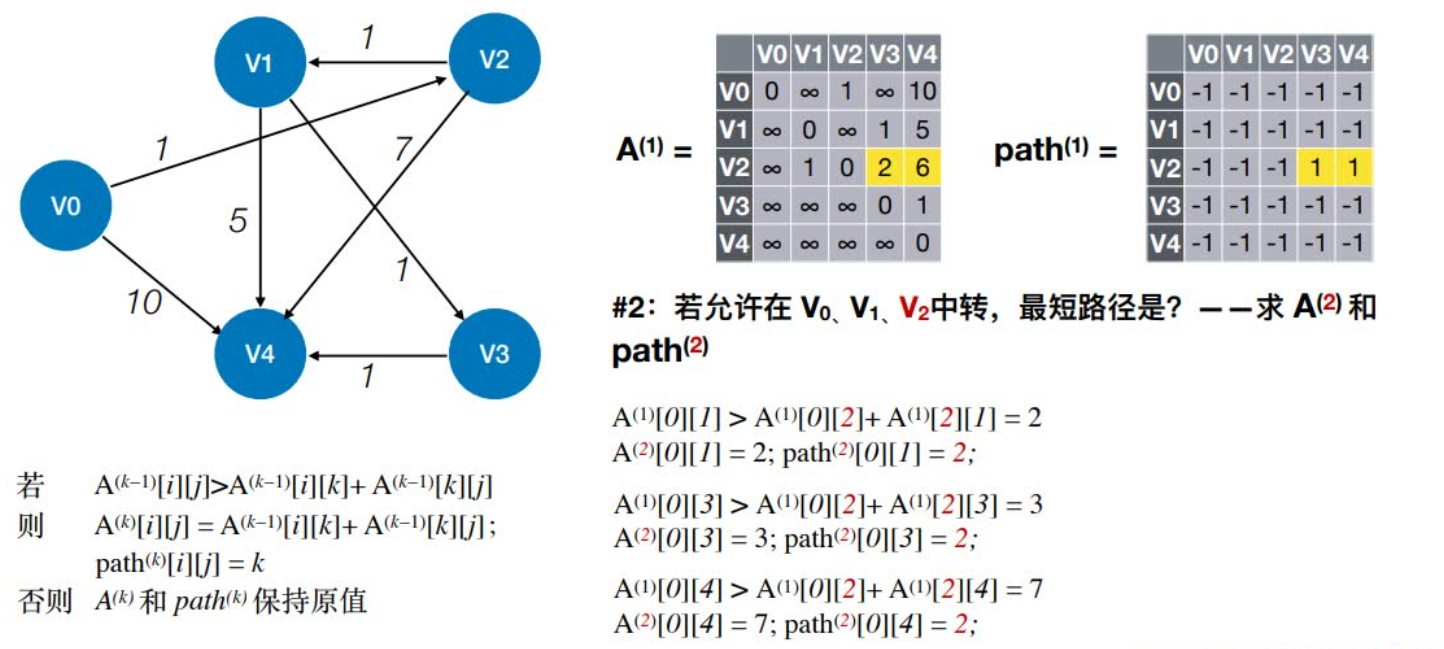
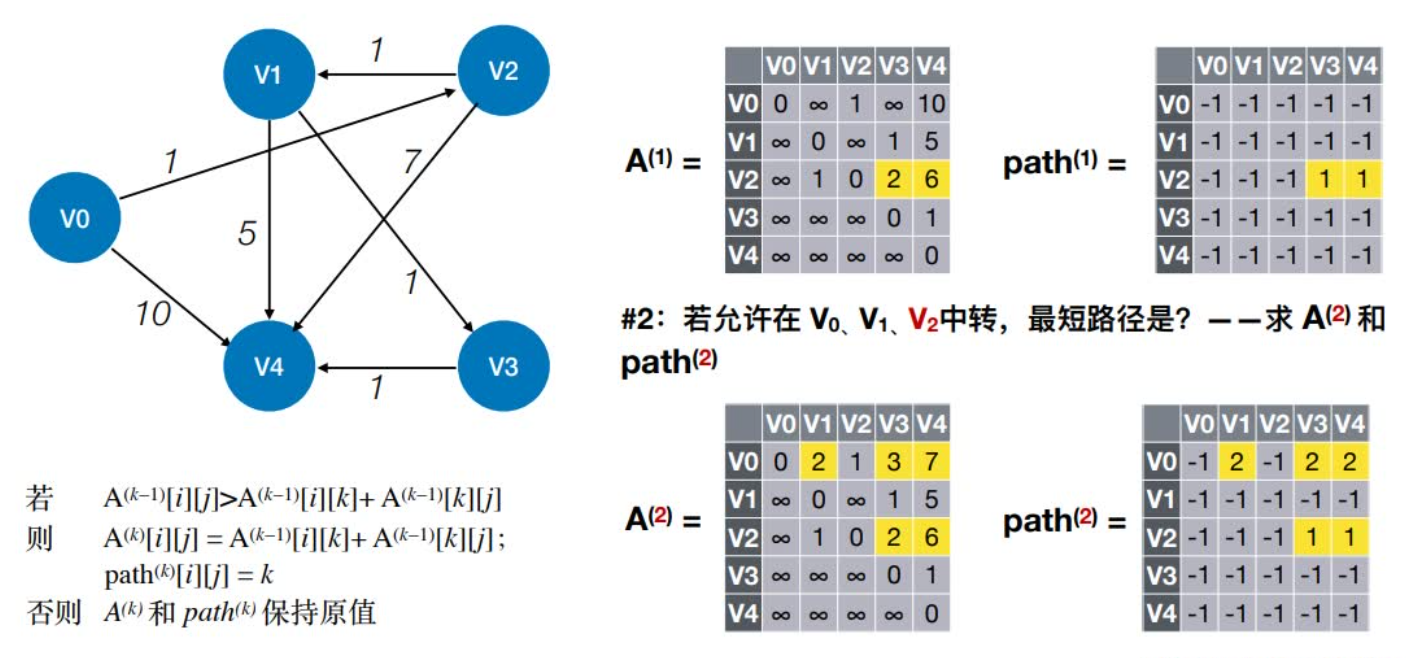
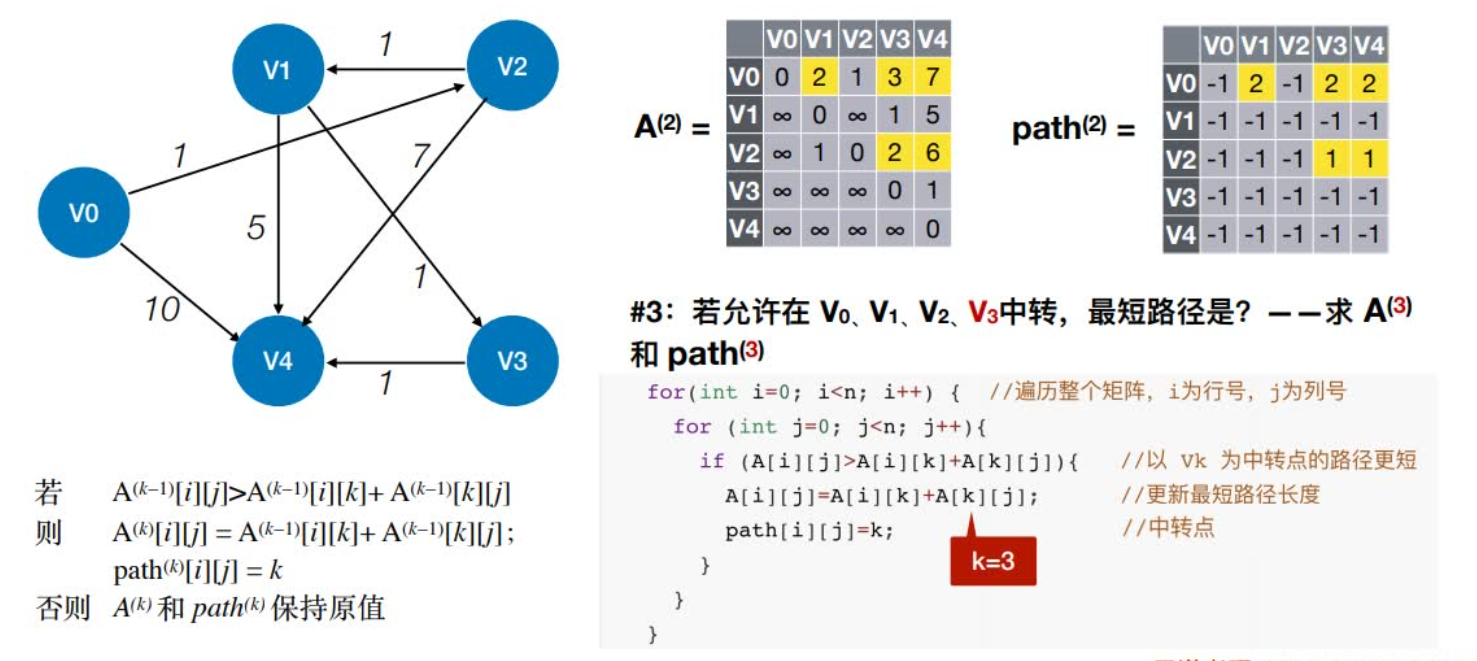
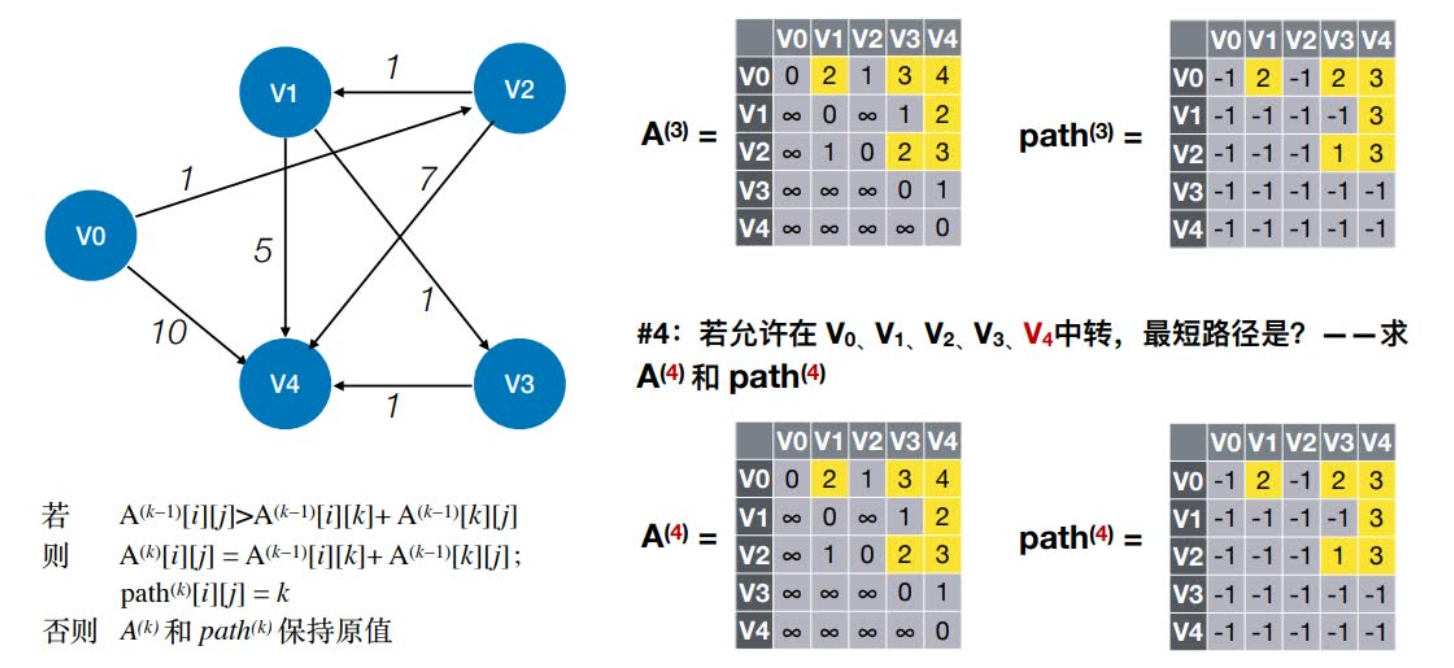
2:若允许在V0、V1、V2中转,最短路径是?
…
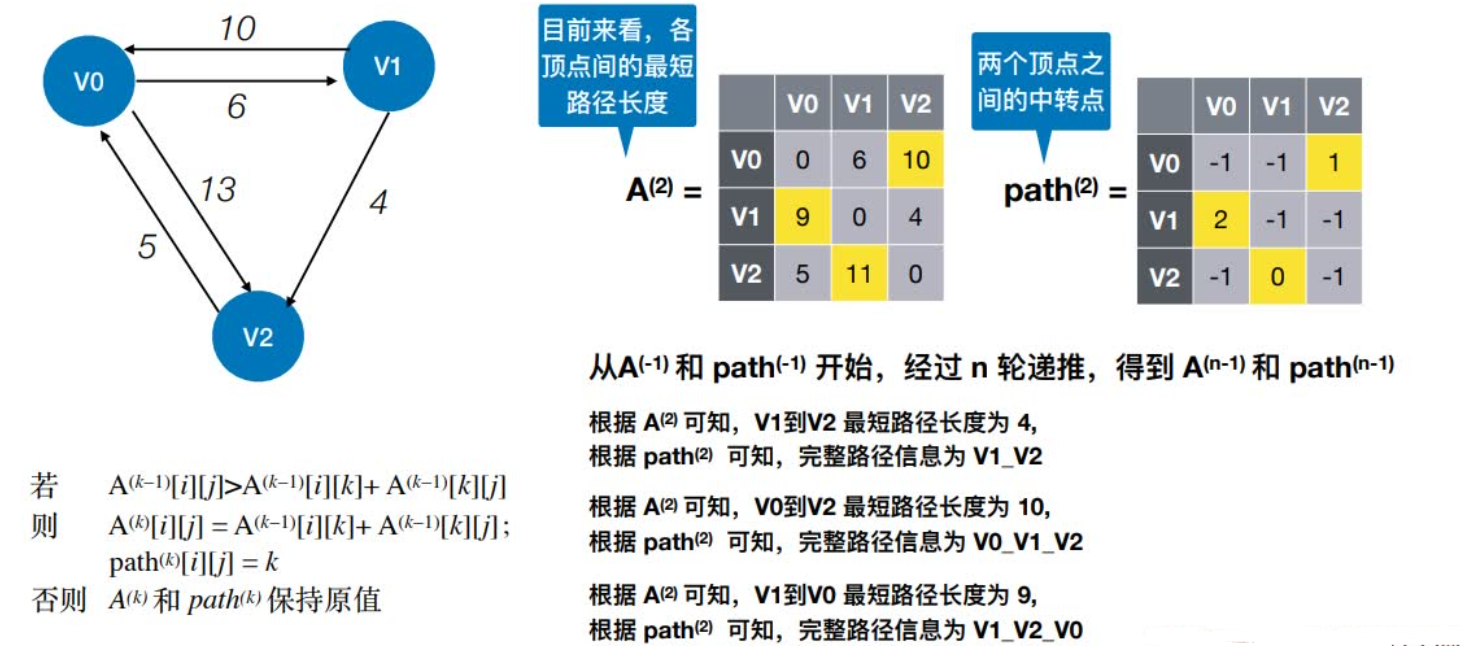
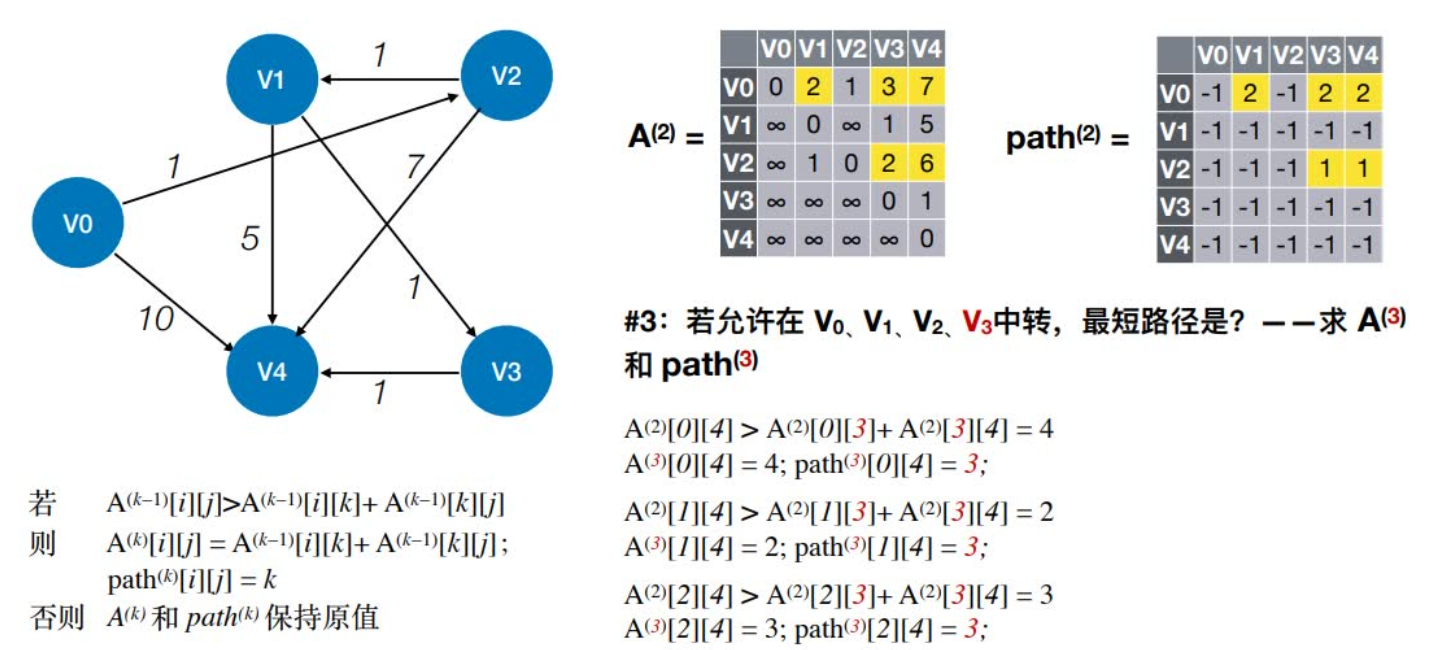
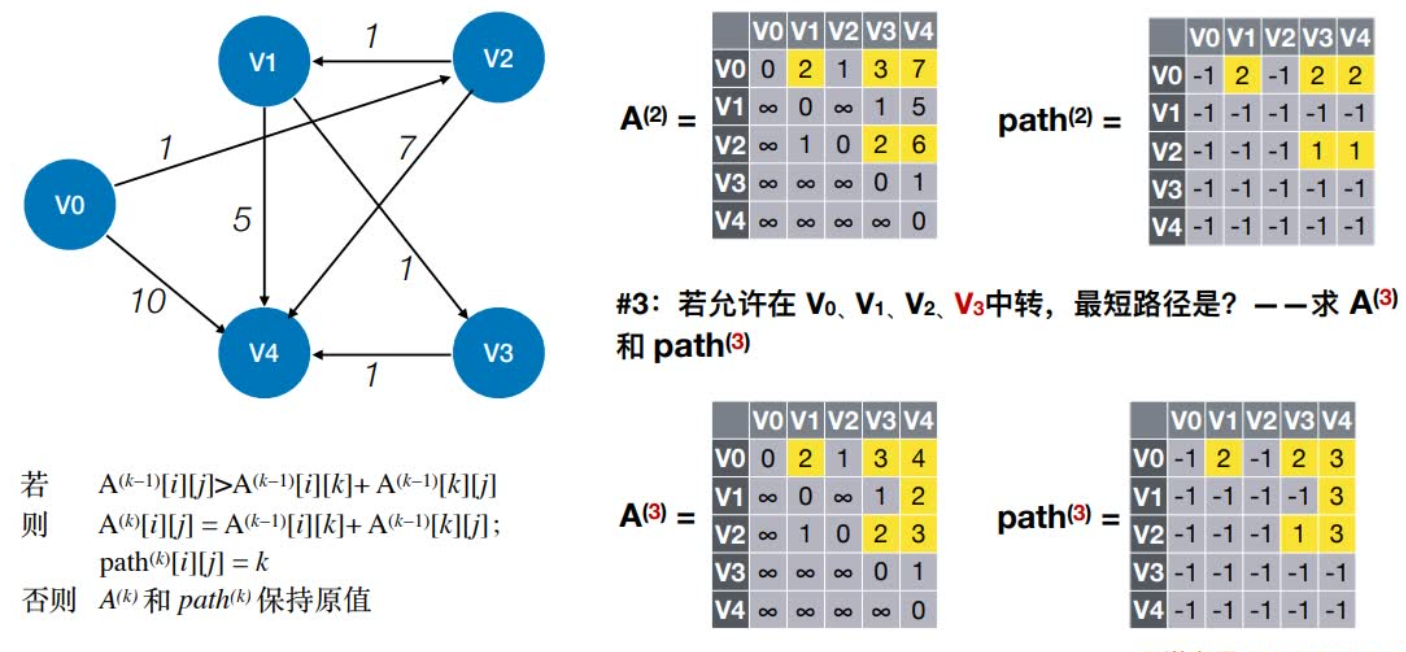
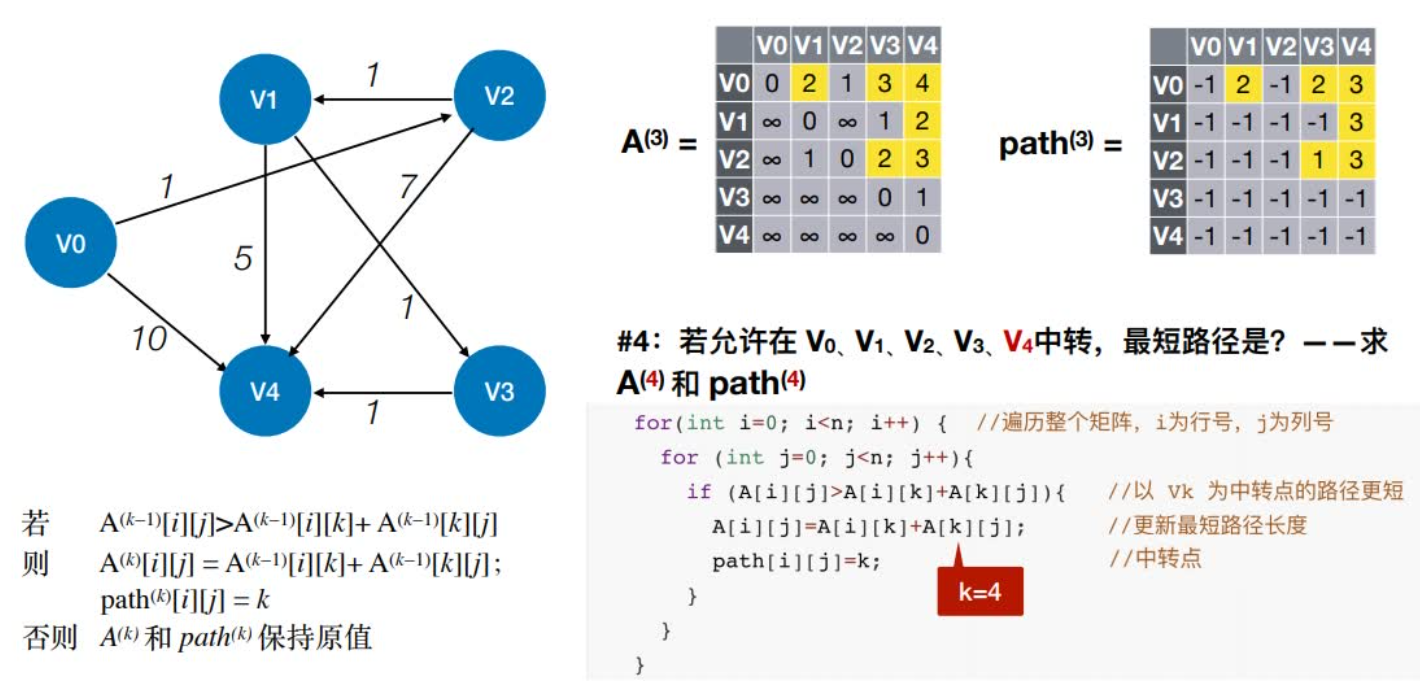
n-1:若允许在V0、V1、V2 ……Vn-1中转,最短路径是?
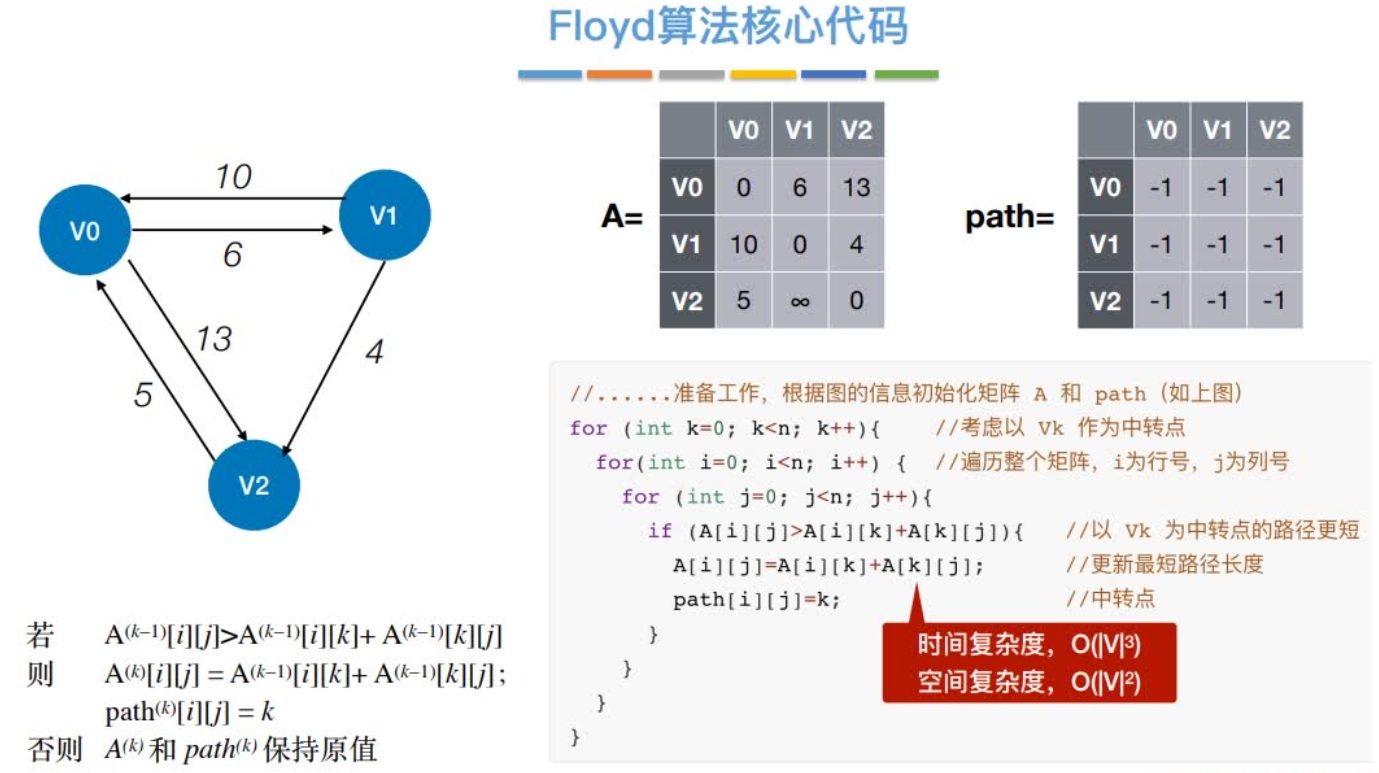
代码实现
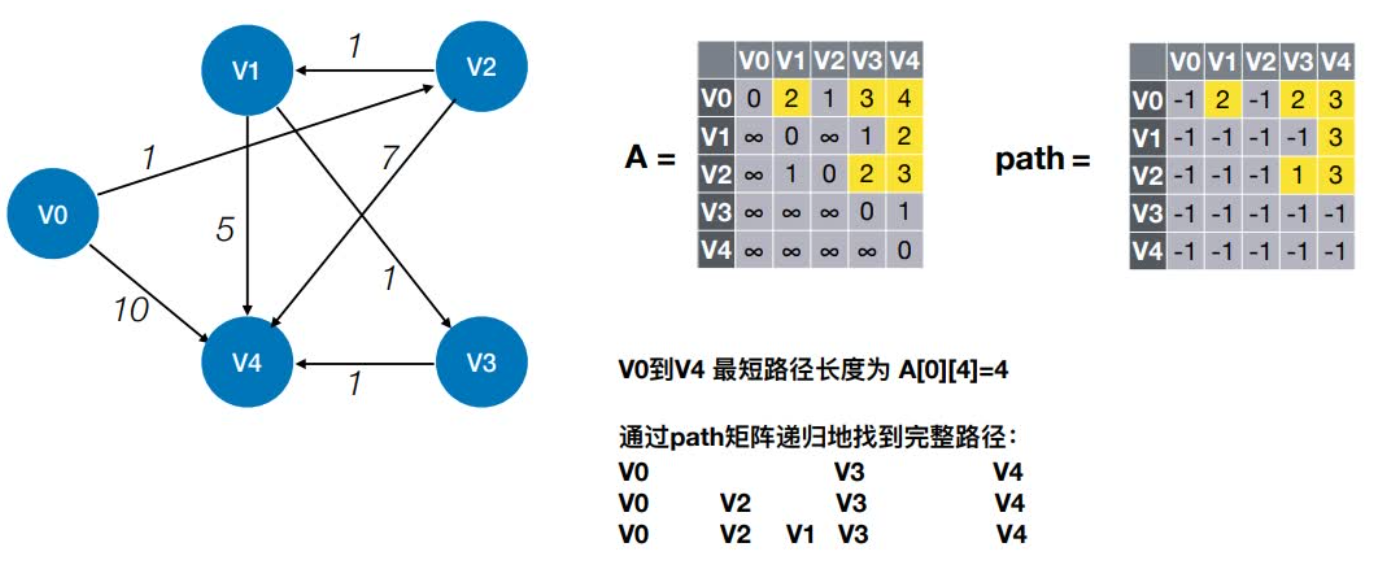
算法实例
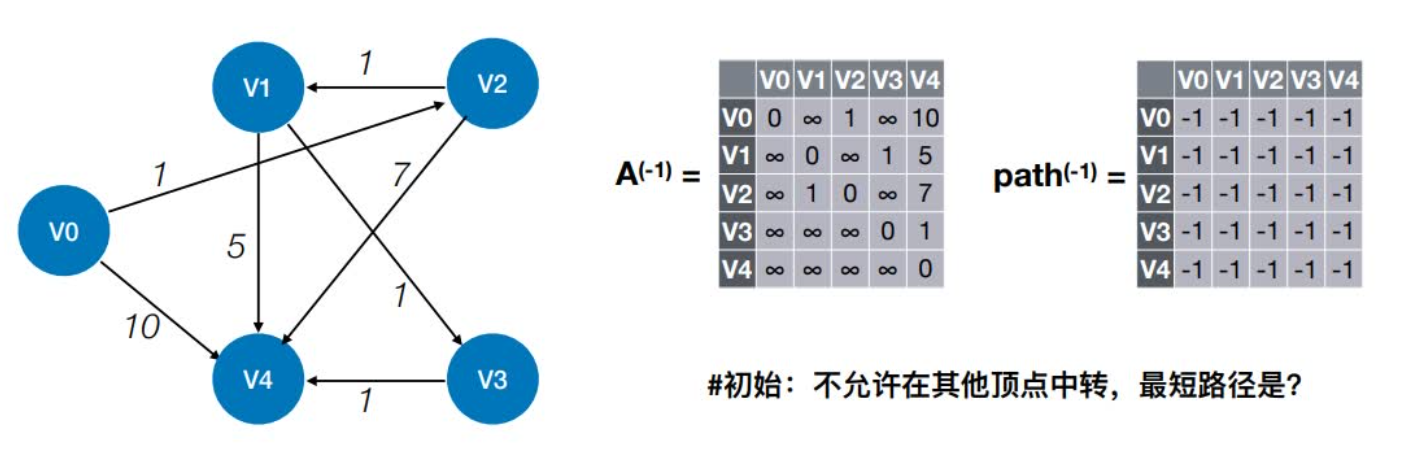
⽤于负权图
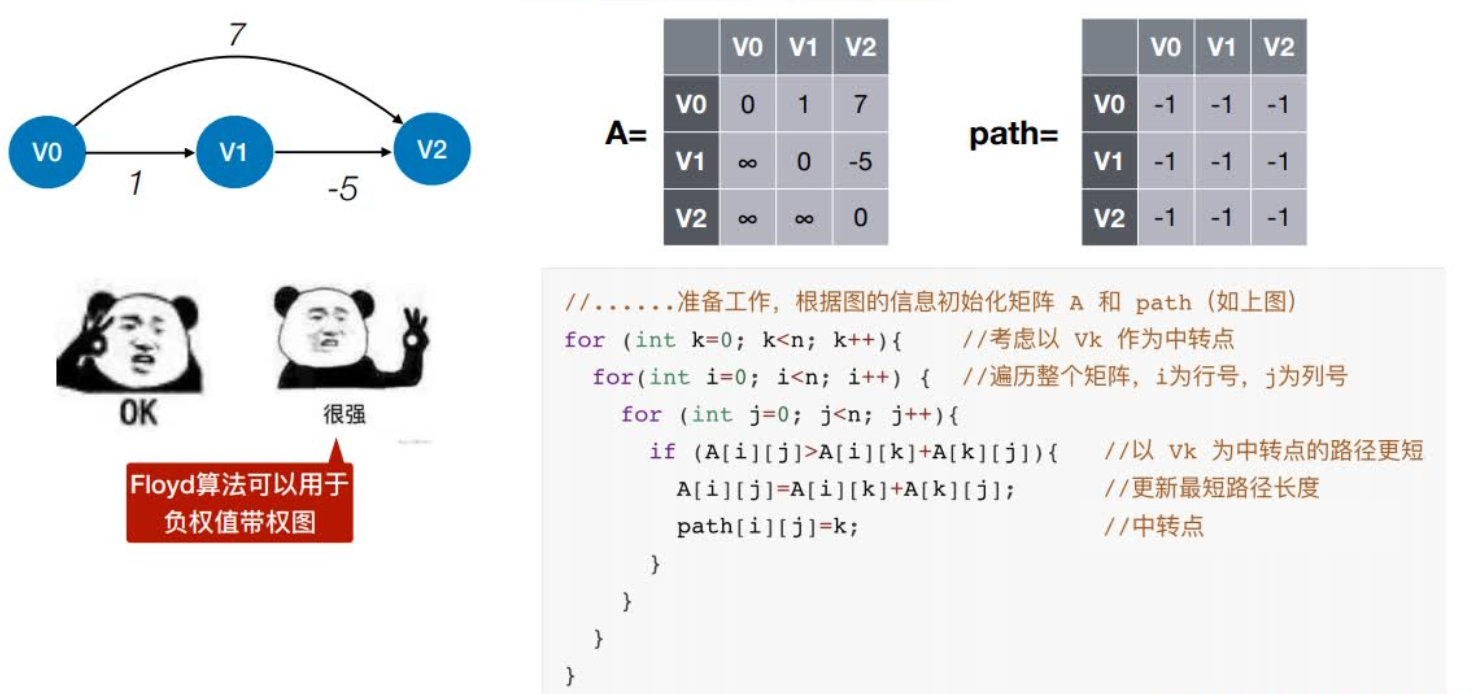
Floyd算法不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径
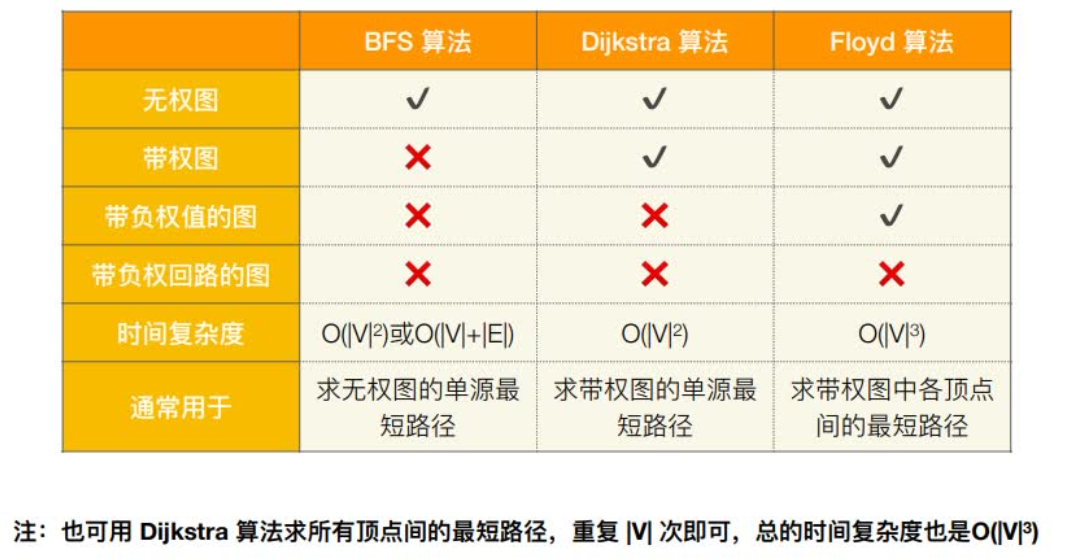
三个算法比较