AcWing 348. 沙漠之王

https://www.acwing.com/problem/content/350/

首先我们了解一下这样一个数学模型（0/1）分数规划：

从题目中得到数学模型，这里要我们求的是一个函数：
Min X = ∑ W / ∑ L

即：
∑ W − X ∗ ∑ L = 0

->f(x)= ∑ W − X ∗ ∑ L
由此我们发现这与上图中的0/1分数规划如出一辙，我们只要将其与Prim算法求最小生成树结合即可

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int N = 1e3 + 10;
const double Dinf = 1e18;
const double eps = 1e-6;
int x[N],y[N],w[N];//x,y是坐标，w[]是地理高度
double dist[N];
bool st[N];
int n;

double calc(int a,int b){//两点之间距离公式
    return sqrt((x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]));
}

bool check(double mid){//Prim算法和0/1分数规划
    //memset(dist,0x3f,sizeof dist);
    fill(dist,dist+n+1,Dinf);//对dis赋值为Dinf,在algorithm头文件中
    //fill(vis,vis+n+1,0);//对vis赋值为0
    memset(st,0,sizeof st);
    dist[1]=0;
    double ans=0;

    for(int i=1;i<=n;i++){
        int t=-1;

        for(int j=1;j<=n;j++)
            if(!st[j] &&(t == -1 || dist[j] < dist[t]))
                t=j;
        st[t]=true;
        ans += dist[t];

        for(int j=1;j<=n;j++){
            if(!st[j] && dist[j] >  abs(w[t]-w[j])- mid* calc(t,j) + eps)
                dist[j]= abs(w[t]-w[j]) - mid* calc(t,j);
        }
    }
    return ans>=0.0;
}

int main(){

    while(scanf("%d",&n),n){
    for(int i=1;i<=n;i++)
        scanf("%d%d%d",&x[i],&y[i],&w[i]);

        double l=0,r=10000001.0;

        while( (r-l) > eps){
            double mid=(l+r)/2;
            if(check(mid)) l=mid;
            else r=mid;
        }
        printf("%.3f\n",l);
    }
    return 0;
}

AcWing 361. 观光奶牛

https://www.acwing.com/problem/content/363/

看完上面的01分数规划，很明显能发现本题就是对其赤裸裸的应用：

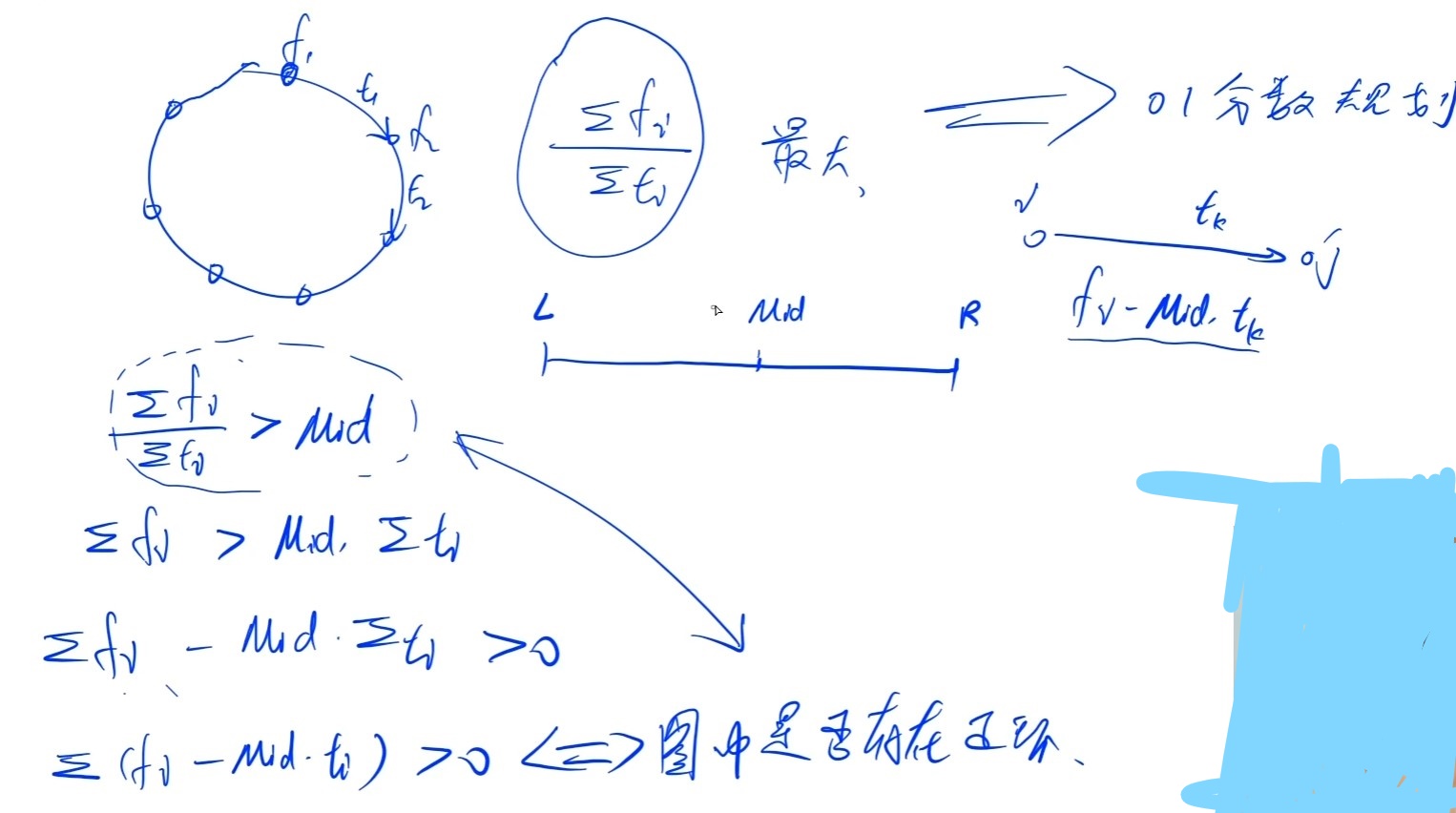
上面这这个图中的f[i]是点权值，t[i]是边权值。
∑ ( f[i] - mid * t[i] ) > 0 ，我们可以将点权与边权合并，即建立一个新图，结构与原图相同，
但是没有点权，边权是f[i] - mid * t[i] .因此∑ ( f[i] - mid * t[i] ) > 0 等价于图中是否存在正环

所以我们可以用spfa判断负环的方法类似地判断正环

#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1010, M = 5010;

int n, m;
int wf[N];//wf即图中的f[]，对应点权
int h[N], e[M], wt[M], ne[M], idx;//wt[]即图中的t[],对应边权
double dist[N];
int q[N], cnt[N];//队列
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, wt[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool check(double mid)
{

    memset(dist, 0x3f, sizeof dist);
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);


    //定义队列，起点进队, 标记进队
    queue<int> q;

    for (int i = 1; i <= n; i ++ ){
//判断正环，只从起点出发，有可能到达不了正环那里，需要一开始就把所有结点放入队列，
//且标记进入了队列降低效率
        q.push(i);
        st[i] = true;
    }

    //队列中的点用来更新其他点到起点的距离
    while (q.size()){
        //取队头，弹队头
        auto t = q.front();
        q.pop();
        //t出队，标记出队
        st[t] = false;

        //更新与t邻接的边
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + wt[i] * mid - wf[j])
            {
                dist[j] = dist[t] + wt[i] * mid - wf[j];//结点j可以通过中间点t降低距离
                cnt[j] = cnt[t] + 1;//那么结点j在中间点t的基础上加一条到自己的边

                if (cnt[j] >= n) return true;//边数不小于结点数，出现正环，函数结束

                if (!st[j])
            //若此时j没在队列中，则进队。已经在队列中了，上面已经更新了数值。重复加入队列降低效率
                {
                    //j进队，标记进队
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return false;//走到这了，函数还没结束，意味着边数一直小于结点数，不存在正环
}


int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> wf[i];//读入点权

    memset(h, -1, sizeof h);
    while(m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    double l = 0, r = 1e6;
    while (r - l > 1e-4)//保留两位小数一般二分到1e-4,三位小数是1e-5
    {
        double mid = (l + r) / 2;
        if (check(mid)) l = mid;//若有正环
        else r = mid;
    }

    printf("%.2lf\n", l);

    return 0;
}

AcWing 1165. 单词环

https://www.acwing.com/problem/content/1167/

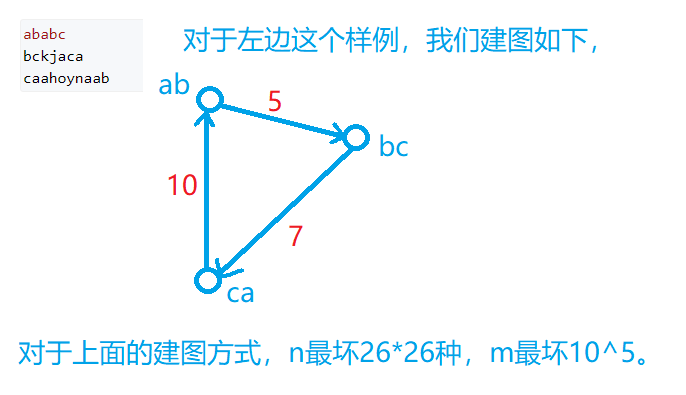
建图: 如果我们将每个字符串看作一个点, 那么边数最坏10^10, 点数10^5, 无论是时间空间任何一种算法必将爆掉
所以我们可以把字符串看成边，字符串的前两字母和后两个字母看成点，这个图和原问题是等价的

max(Σwi / k)
- 确定二分区间
0 ~ 1000 * k / k
- 求最大值得到check不等式
Σwi / k > mid
=> Σwi > k * mid
=> Σwi - k * mid > 0
=> Σ(wi - mid * 1) > 0 -> 即正环 最长路边数大于n-1
优化点1: 如果mid为0的时候, wi都为负, 最终l = r = 0, 平均长度为0, 即无环, 直接输出no solution

当超时时：根据y总的经验，我们不妨int count = 0;//所有点被更新的总次数，if ( ++ count > 10000) return true; // 经验上如果所有点更新总次数>10000,说明存在正环

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 700, M = 100010;

int n;//边的数量
int h[N], e[M], w[M], ne[M], idx;
double dist[N];
int q[N], cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool check(double mid)//spfa判断正环
{
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);//将所有边数清空
     //距离不用清空，因为能否找到负环和距离没有关系

    int hh = 0, tt = 0;
    for (int i = 0; i < 676; i ++ )
    {
        q[tt ++ ] = i;
        st[i] = true;
    }

    int count = 0;///所有点被更新的总次数
    while (hh != tt)//当队列不空时
    {
        int t = q[hh ++ ];
        if (hh == N) hh = 0;
        st[t] = false;

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] < dist[t] + w[i] - mid)
            {
                dist[j] = dist[t] + w[i] - mid;
                cnt[j] = cnt[t] + 1;
                if ( ++ count > 10000)return true;

//经验上如果所有点更新总次数>10000(点数最多是676，10000远大于676，已经遍历了这么多次，经验上应有正环)
                if (cnt[j] >= N) return true;//存在正环
                if (!st[j])
                {
                    q[tt ++ ] = j;
                    if (tt == N) tt = 0;//因为是循环队列。当到N时，再折到开头
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

int main()
{
    char str[1010];
    while (scanf("%d", &n), n)
    {
        memset(h, -1, sizeof h);
        idx = 0;
        for (int i = 0; i < n; i ++ )
        {
            scanf("%s", str);
            int len = strlen(str);
            if (len >= 2)
            {
                int left = (str[0] - 'a') * 26 + str[1] - 'a';//将前两个字母当成一个26进制的数
                int right = (str[len - 2] - 'a') * 26 + str[len - 1] - 'a';
                add(left, right, len);
            }
        }

        if (!check(0)) puts("No solution");//若0都构不成环，无解
        else
        {
            double l = 0, r = 1000;
            while (r - l > 1e-4)
            {
                double mid = (l + r) / 2;
                if (check(mid)) l = mid;
                else r = mid;
            }

            printf("%lf\n", r);
        }
    }

    return 0;
}