给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1 到 N。
问从顶点 1 开始,到其他每个点的最短路有几条。
输入格式
第一行包含 2 个正整数 N,M,为图的顶点数与边数。
接下来 M 行,每行两个正整数 x,y,表示有一条顶点 x 连向顶点 y 的边,请注意可能有自环与重边。
输出格式
输出 N 行,每行一个非负整数,第 i 行输出从顶点 1 到顶点 i 有多少条不同的最短路,由于答案有可能会很大,你只需要输出对 100003 取模后的结果即可。
如果无法到达顶点 i 则输出 0。
数据范围
1≤N≤10^5,
1≤M≤2×10^5
输入样例:
5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5
输出样例:
1
1
1
2
4
要求最短路计数首先满足条件是不能存在值为0的环,因为存在的话那么被更新的点的条数就为INF了。
要把图抽象成一种最短路树(拓扑图)。
求最短的算法有以下几种(本人学过的)
BFS 只入队一次,出队一次。可以抽象成拓扑图, 因为它可以保证被更新的点的父节点一定已经是最短距离了,并且这个点的条数已经被完全更新过了。这个性质是核心性质。
dijkstra 每个点只出队一次。也可以抽象成拓扑图, 同理由于每一个出队的点一定已经是最短距离,并且它出队的时候是队列中距离最小的点,这就代表他的最短距离条数已经被完全更新了,所以构成拓扑性质。
bellman_ford算法 spfa 本身不具备拓扑序,因为更新它的点不一定是最短距离,所以会出错。举个例子
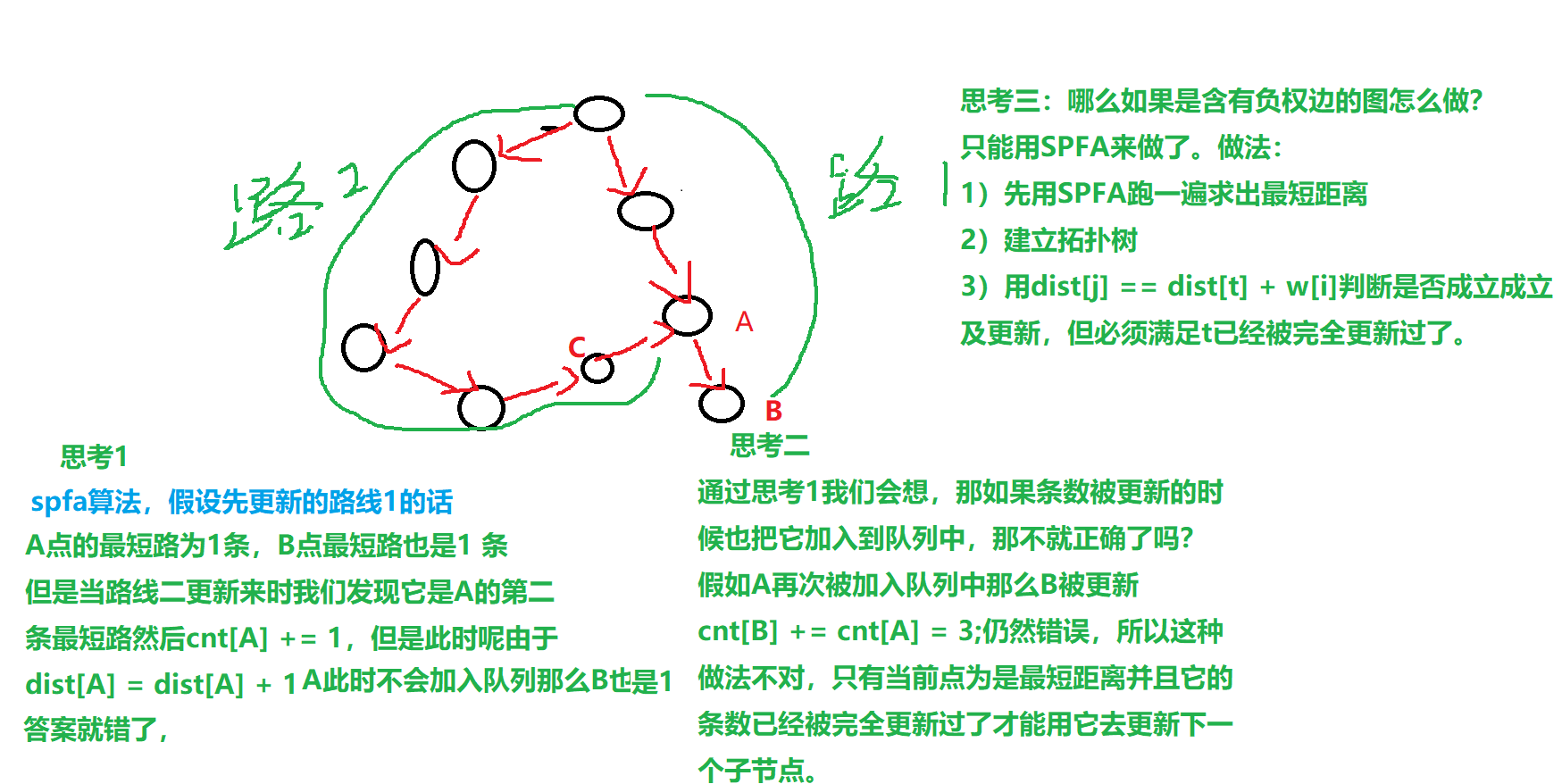
但如果图中存在负权边只能用该算法做,也能做但是比较麻烦
先跑一遍spfa找到每个点的最短距离,把最短路拓扑树建立出来,看哪一条边dist[j] == dist[t] + w[i],然后更新它。
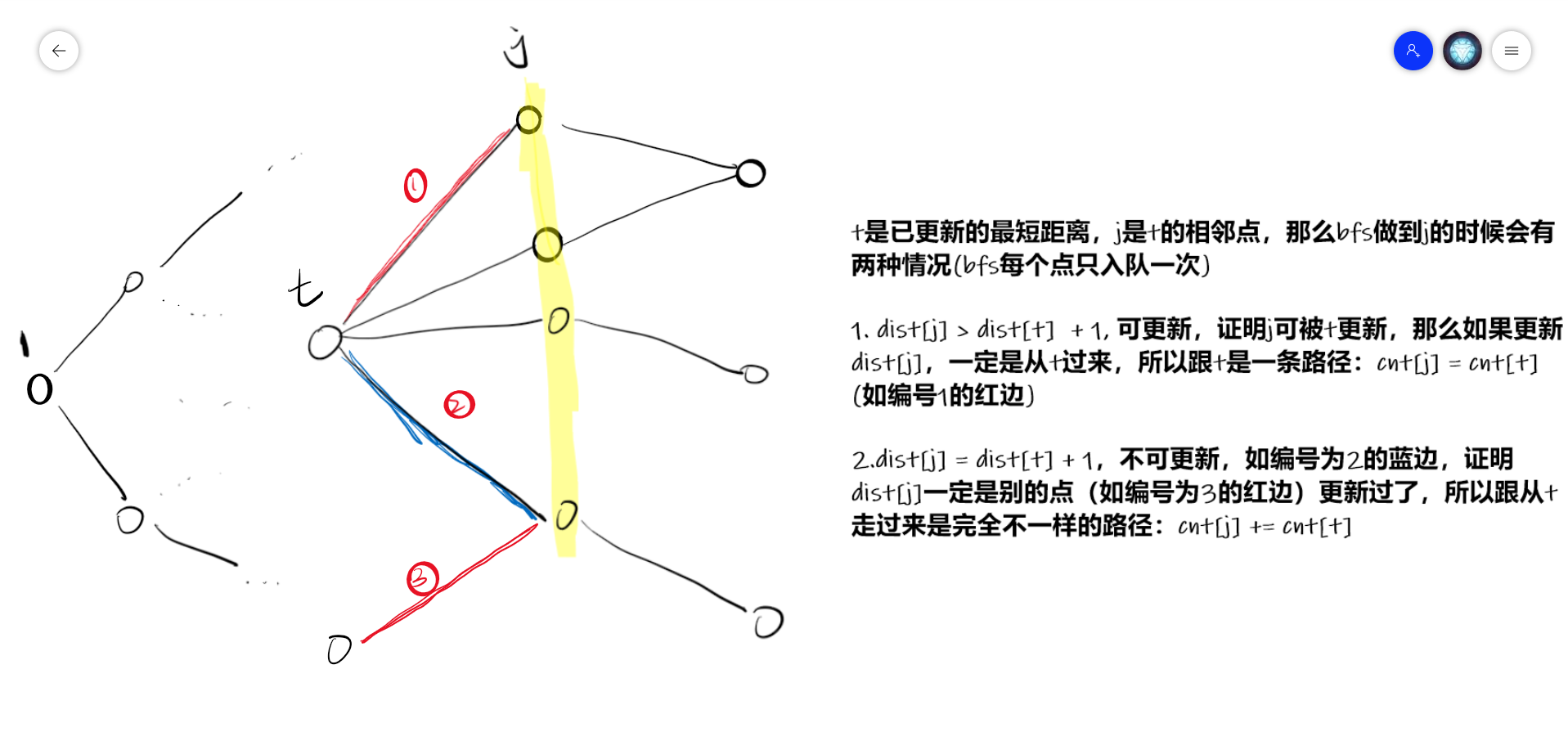
BFS:
/*
根据路径中指向目标节点的最后一个节点的编号来分类
dp问题求解的前提条件就是满足拓步序,这道题可能存在环,不能用dp求解
存下每个点是由那个点更新过来的dist[j]=dist[t]+w[i];
*/
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N = 100010, M = 400010, mod = 100003;
int n, m;
int head[N], e[M], ne[M], idx;
int dist[N], cnt[N]; // dist[i]表示从1到i所有路径中的最短路径,cnt[i],从1到达i的最短路径的条数
int q[N];
void add(int a, int b) {
e[idx] = b,ne[idx] = head[a],head[a] = idx ++;
}
// 不能存在长度为0的环
void bfs() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
cnt[1] = 1;
int hh = 0, tt = 0;
q[0] = 1;
while (hh <= tt) {
int t = q[hh ++];
// 记录一下这个点被更新时,更新他的前驱,可以得到一棵树,树是具有拓扑序的
// 规定一个点只能被一个前驱更新(如果有多个最短路一样的前驱更新他,也认为只有一个)
for (int i = head[t]; i != -1; i = ne[i]) {
int j = e[i]; // 枚举t的所有临边(t可以更新到的点)
if (dist[j] > dist[t] + 1) {
dist[j] = dist[t] + 1; // 如果用t来更新j,那t一定已经求得最小值
cnt[j] = cnt[t]; // 如果更新了这条路径的话, 那就跟t是同一条路
q[++ tt] = j; // 每个点只入队一次
}
else if (dist[j] == dist[t] + 1) cnt[j] = (cnt[j] + cnt[t]) % mod;
}
}
}
int main() {
cin >> n >> m;
memset(head, -1, sizeof head);
while (m --){
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
bfs();
for (int i = 1; i <= n; i ++) cout << cnt[i] << endl;
return 0;
}
堆优化版的dijkstra():
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int , int>PII;
const int N = 100010 , M = 400010 , MOD = 100003;
int n , m;
int h[N] , e[M] , ne[M] , idx;
int dis[N] , cnt[N];
bool st[N];
void add(int a , int b)
{
e[idx] = b , ne[idx] = h[a] , h[a] = idx ++ ;
}
void dijkstra()
{
memset(dis , 0x3f , sizeof dis);
dis[1] = 0;
cnt[1] = 1;
priority_queue<PII , vector<PII> , greater<PII>> heap;
heap.push({0 , 1});
while(!heap.empty())
{
auto t = heap.top();
heap.pop();
int ver = t.second , distance = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver] ; i != -1 ; i = ne[i])
{
int j = e[i];
if(dis[j] > distance + 1)
{
dis[j] = distance + 1;
cnt[j] = cnt[ver];
heap.push({dis[j] , j});
}
//只有当当前值可以被更新时才加入到队列当中,(bfs同理)
else if(dis[j] == distance + 1) cnt[j] = (cnt[j] + cnt[ver]) % MOD;
}
}
}
int main()
{
cin >> n >> m;
memset(h , -1 , sizeof h);
while(m -- )
{
int a , b;
cin >> a >> b;
add(a , b) , add(b , a);
}
dijkstra();
for(int i = 1 ; i <= n ; i ++ ) cout << cnt[i] << endl;
return 0;
}
AcWing 383. 观光:
https://www.acwing.com/problem/content/385/
我们发现在上一题的基础上,只用一维的distdist和cntcnt数组并不能表示最短和次短两个状态,所以多开一维:
用状态00表示最短,用状态11表示次短,所以同一个点就会有两种不同的状态,可以将着两种状态看作是不同的点来处理
设状态dist[i][0,1]dist[i][0,1]表示初始城市SS到城市ii的最短距离和次短距离
cnt[i][0,1]cnt[i][0,1]表示城市SS到城市ii的最短路径和次短路经的条数
初始时,dist[S][0]dist[S][0]为00,cnt[S][0]cnt[S][0]为1
枚举城市t可通往的城市jj时,有四种情况:(dijkstra只要dist发生改变,就将该点入队)
dist[j][0]>dist[v][type]+w[i]:
当前最短路变成次短路,更新最短路,将最短路和次短路加入优先队列,到达j的最短路个数和到达t是一样的 :
cnt[j][0]=cnt[t][type]cnt[j][0]=cnt[t][type]
dist[j][0]=dist[v][type]+w[i] :找到一条新的最短路,更新最短路条数
到达j的最短路个数应该加上到达tt的最短路个数,从t经过的最短路,在j上经过的时候也是最短路:
cnt[j][0]+=cnt[t][type]cnt[j][0]+=cnt[t][type]
dist[j][1]>dist[v][type]+w[i]:找到一条更短的次短路,覆盖掉当前次短路,加入优先队列
到达j的最短路个数和到达t是一样的 :
cnt[j][1]=cnt[t][type]cnt[j][1]=cnt[t][type]
dist[j][1]=dist[v][type]+w[i] :找到一条新的次短路,更新次短路条数
到达j的最短路个数应该加上到达t的最短路个数,从t经过的最短路,在j上经过的时候也是最短路:
cnt[j][1]+=cnt[t][type]cnt[j][1]+=cnt[t][type]
最后到F城市的次短路径如果比最短路径恰好多1,满足题目要求,则把这样的路径条数加到答案里
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<queue>
using namespace std;
const int N = 1010,M = 10010;
int h[N],e[M],ne[M],w[M],idx;
//状态0表示的是求最下,状态1表示求的是次小
int cnt[N][2]; //cnt[i][0]表示从1到i的最短历经条数,cnt[i][1]表示从1到i的次短路径条数
int dist[N][2]; //dist[i][0]表示从1到i的最短路径,d[i][1]表示从1到i的次短路径
bool st[N][2]; //与上面同理
int n,m,S,T; //S表示起点,T表示终点
struct node{ //小根堆,重载大于号
int id,type,distance; //分别是编号,状态,和当前点到起点的最小或次小距离
bool operator> (const node& a) const{ //从大到小排序
return distance > a.distance;//小根堆重载大于,大根堆重载小于,下文定义小根堆的时候会用
}
};
void add(int a,int b,int c){
w[idx] = c;
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int dijkstra(){
memset(st, 0, sizeof st);
memset(dist, 0x3f, sizeof dist);
memset(cnt, 0, sizeof cnt);
priority_queue<node,vector<node>,greater<node>> heap;//结构体类型
dist[S][0] = 0;
cnt[S][0] = 1;
heap.push({S,0,0});
while(heap.size()){
node t = heap.top();
heap.pop();
int ver = t.id , type = t.type , distance = t.distance;
if(st[ver][type]) continue;
st[ver][type] = true;
for(int i = h[ver];i != -1;i = ne[i]){
int j = e[i];
//以下if中的dist[ver][type]也可写成distance,这两者是等价的
//先考虑最短的情况(大于、等于)
if(dist[j][0] > dist[ver][type] + w[i]){
//dist[j][0]成为次小,先要赋值给dist[j][]中次小的状态
dist[j][1] = dist[j][0]; cnt[j][1] = cnt[j][0];
heap.push({j, 1, dist[j][1]}); //发生改变就要入队
dist[j][0] = dist[ver][type] + w[i]; cnt[j][0] = cnt[ver][type]; //直接转移
heap.push({j,0,dist[j][0]});
}else if(dist[j][0] == dist[ver][type] + w[i]){
cnt[j][0] += cnt[ver][type]; //从t经过的最短路,在j上经过的时候也是最短路
//轮到枚举次小
}else if(dist[j][1] > dist[ver][type] + w[i]){
dist[j][1] = dist[ver][type] + w[i];
cnt[j][1] = cnt[ver][type];
heap.push({j, 1, dist[j][1]});
}else if(dist[j][1] == dist[ver][type] + w[i]){
cnt[j][1] += cnt[ver][type]; //从t经过的最短路,在j上经过的时候也是最短路
}
}
}
int res = cnt[T][0];
//最后还要特判以下最小和次小的路径之间是否相差1符合要求
if (dist[T][0] + 1 == dist[T][1]) res += cnt[T][1];
return res;
}
int main(){
int t;
cin >> t;
while(t--){
memset(h,-1,sizeof h);
cin >> n >> m;
for(int i = 0;i < m;++i){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
scanf("%d%d",&S,&T);
cout << dijkstra() << endl;
}
return 0;
}

