基础数论笔记
一直觉得数论好容易忘,想把数论学的基础知识给自己整理一遍,看一遍也能算复习一遍。
理解和参考了算法竞赛进阶指南与基础课
数论其实真的好好玩啊,如果不是急着功利一点的话其实还是会愿意自学一下的
一、质数
Ⅰ、判断质数(试除法)
试除法判断质数
给定 $n$个正整数 $a_i$,判定每个数是否是质数。试除法判断质数
板子
#include<iostream>
#include<cstdio>
using namespace std;
bool is_prime(int n)
{
if(n<2) return false;
for(int i=2;i<=n/i;i++)
if(n%i==0) return false;
return true;
}
int main()
{
int T;cin>>T;
while(T--){
int n;cin>>n;
if(is_prime(n)) puts("Yes");
else puts("No");
}
}
Ⅱ、分解质因数
给定 n 个正整数 $a_i$,将每个数分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。
原理:算数基本定理
算数基本定理:任何一个大于1的自然数N都可以唯一分解成有限个质数的乘积。
形式:$N=p_1^{a_1} …p_k^{a_k}$两个推论:约数个数与约数之和
板子
#include<iostream>
#include<cstdio>
using namespace std;
void divide(int x)
{
for(int i=2;i<=x/i;i++){
if(x%i==0){
int cnt=0;
while(x%i==0)x/=i,cnt++;
cout<<i<<' '<<cnt<<endl;
}
}
if(x>1) cout<<x<<' '<<1<<endl;
cout<<endl;
}
int main()
{
int n;
cin>>n;
while(n--){
int x;
scanf("%d",&x);
divide(x);
}
}
Ⅲ、筛质数(线性筛法)
给定一个正整数 $n$,请你求出 $1∼n $中质数的个数。
原理
保证每个合数只被它的最小质因数筛掉,这样避免重复筛除后时间复杂度可以达到$O(n)$
比如$12=2\*6=3*4$,那么只会用$2$去筛除,枚举到$i=4$的时候只会筛除$8$
板子
#include<iostream>
using namespace std;
const int N=1e6+10;
int get_cnt(int n)
{
int prime[N],cnt=0;
bool st[N]={false};
for(int i=2;i<=n;i++){
if(!st[i]) prime[++cnt]=i;
for(int j=1;prime[j]<=n/i;j++){
st[i*prime[j]]=true;
if(i%prime[j]==0) break;
}
}
return cnt;
}
int main()
{
int n;cin>>n;
printf("%d\n",get_cnt(n));
return 0;
}
二、约数
Ⅰ、求约数(试除法)
给定 n 个正整数 $a_i$,对于每个整数 $a_i$,请你按照从小到大的顺序输出它的所有约数。
板子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> get_divider(int n)
{
vector<int> res;
for(int i=1;i<=n/i;i++){
if(n%i==0){
res.push_back(i);
if(i!=n/i) res.push_back(n/i);
}
}
sort(res.begin(),res.end());
return res;
}
int main()
{
int T;cin>>T;
while(T--){
int n;cin>>n;
vector<int> ans=get_divider(n);
for(auto x:ans) cout<<x<<' ';
puts("");
}
return 0;
}
Ⅱ、约数个数
给定 $n$ 个正整数 $a_i$,请你输出这些数的乘积的约数个数,答案对 $1e9+7$ 取模。
原理:算数基本定理推论1
证明:
假设数$N=p_{1}^{a_{1}} \cdots p_{k}^{a_{k}}$
假设任意一个约数$Q=p_1^{0\sim a_1}…p_k^{0\sim a_k}$,由算数基本定理,
对于任意$a_{1\sim k}$位置的选择,都有唯一的一个$Q$与之对应。
而数$N$的约数个数就是$Q$的个数,因此由乘法原理
约数个数$cnt=(a_1+1)\*(a_2+1)\*…(a_k+1)$
结论:算某个数的约数个数,先分解质因数,再把他们的幂+1乘起来。
板子
#include<iostream>
#include<cstdio>
#include<unordered_map>
using namespace std;
const int mod=1e9+7;
unordered_map<int,int> p;
void divide(int n)
{
for(int i=2;i<=n/i;i++)
if(n%i==0)
while(n%i==0){
n/=i;
p[i]++;
}
if(n>1) p[n]++;
}
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++){
int x;cin>>x;
divide(x);
}
int res=1;
for(auto k:p) res=(1ll*res*(k.second+1))%mod;
cout<<res<<endl;
return 0;
}
Ⅲ、约数之和
给定 n 个正整数 $a_i$,请你输出这些数的乘积的约数之和,答案对$1e9+7$取模。
原理:算数基本定理推论2
证明:
假设数$N=p_1^{a_1} …p_k^{a_k}$
假设任意一个约数$Q=p_1^{0\sim a_1}…p_k^{0\sim a_k}$,由算数基本定理,
对于任意$a_{1\sim k}$位置的选择,都有唯一的一个$Q$与之对应。
而数$N$的约数之和就是$Q$的可能性的和,因此由乘法原理
约数之和$ans=(p_1^{0}+p_1^{1}+p_1^{2}+…+p_1^{a_1})\*(p_2^{0}+p_2^{1}+p_2^{2}+…+p_2^{a_2})\*…\*(p_k^{0}+p_k^{1}+p_k^{2}+…+p_k^{a_k})$
结论:算某个数的约数之和,先分解质因数,分别相加他们的所有可能值,再算出乘积。
板子
#include<iostream>
#include<unordered_map>
using namespace std;
const int mod=1e9+7;
unordered_map<int,int> p;
void divide(int n)
{
for(int i=2;i<=n/i;i++)
if(n%i==0)
while(n%i==0){
n/=i;
p[i]++;
}
if(n>1) p[n]++;
}
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++){
int x;cin>>x;
divide(x);
}
int ans=1;
for(auto k:p){
int a=k.first,b=k.second;
int res=1;
for(int i=1;i<=b;i++) res=(1ll*res*a+1)%mod;//秦九韶算法
ans=(1ll*ans*res)%mod;
}
cout<<ans<<endl;
return 0;
}
Ⅳ、最大公约数(GCD)
给定 $n$ 对正整数 $a_i,b_i$,请你求出每对数的最大公约数。
原理
1、一些定义
$a,b$的最大公约数记作$gcd(a,b)$,$a,b$的最小公倍数记作$lcm(a,b)$
定理:$\forall a,b\in N,gcd(a,b)\*lcm(a,b)=a\*b$
证明:
设$d=gcd(a,b),a_0=a/d,b_0=b/d $
$lcm(a,b)=lcm(a_0\*d,b_0\*d)$
$ =lcm(a_0,b_0)\*d$
$=a_0\*b_0*d=a\*b/d=a\*b/gcd(a,b)$
两数的乘积等于两数最小公倍数和最大公约数的乘积
2、更相减损术
定理:$\forall a,b\in{N},a\ge{b},有\gcd(a,b)=\gcd(b,a-b)=\gcd(a,a-b)$
证明:
对$(a,b)$的任意公约数$d$,有$d|a,d|b$,所以$d|(a-b)$
综上$(a,b)$与$(b,a-b)$的公约数集合相同,因此$\gcd(a, b)=\gcd(a,a-b)=\gcd(b,a-b)$
证毕
3、欧几里得算法
定理:$\forall{a,b}\in{N},b\ne 0, \gcd(a, b)=\gcd(b,a \bmod b) $
证明:
若$a<b,\gcd(b,a)=\gcd(a,b)$
若$a\ge b$,设$a=q\*b+r,r=a\bmod b$,对$(a,b)$的任意公约数$d$,有$d|a,d|q\*b$
因此有$d|(a-q\*b)\Leftrightarrow d|r$,因此$d$也是$(b,r)$的公约数。
综上$(a,b)$与$(b,a\bmod b)$的公约数集合相同,有$\gcd(a, b)=\gcd(b,a \bmod b)$
证毕
板子(欧几里得算法)
高精度运算可以用更相减损术来实现
#include<iostream>
using namespace std;
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int main()
{
int T;cin>>T;
while(T--){
int a,b;cin>>a>>b;
cout<<gcd(a,b)<<endl;
}
return 0;
}
三、欧拉函数
Ⅰ、定义
$1 \sim N $ 中与 $N$ 互质的数的个数被称为欧拉函数,记为 $ϕ(N)$
若在算数基本定理中,$N = p_1^{a_1}p_2^{a_2}…p_m^{a_m}$,
则:$ϕ(N)$ = $N \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times …\times \frac{p_m-1}{p_m}$
Ⅱ、欧拉函数的证明
设$p$为$N$的质因子,则$1\sim{N}$中$p$的倍数有$2p,3p,…,(N/p)*p$共$N/p$个数。
同理设$q$为$N$的质因子,则$1\sim N$有$q$的倍数$N/q$个。
若从与$N$的互质的数的集合中扣除全部$p$与$q$的倍数,则对于$p*q$的倍数会被多扣一次。
因此由容斥原理可得:
除去$p,q$的所有倍数与$N$的互质的数的集合个数
$cnt=N-\frac{N}{p}-\frac{N}{q}+\frac{N}{pq}=N(1-\frac{1}{p})(1-\frac{1}{q})$
类似地可以对所有质因数这样做,最后得到$ϕ(N)$ = $N \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times …\times \frac{p_m-1}{p_m}$
证毕
Ⅲ、欧拉函数的一些性质
参考了这篇博客 欧拉函数及其性质
性质1:$sum=n*\varphi(n)/2 $
$\forall{n}>1,1\sim n$中与$n$互质的数的和为$ n* \varphi(n)/2$
证明:
首先证明:若有$\gcd(n,x)=1$,则有$\gcd(n,n-x)=1$
反证法:假设存在$\gcd(n,x)=1$,$\gcd(n,n-x)=k$
则$n\%k=0,(n-x)\%k=0$,所以$x\%k=0$,$\gcd(n,x)=k$,与假设矛盾
$\gcd(n,x)=\gcd(n,n-x)=1$
因此与$n$互质的数$(x,n-x)$是两两成对出现的,他们的和就等于$n$
所以与$n$互质的数的和就等于与$n$互质的数的个数的一半乘以$n$
即$sum=n*\varphi(n)/2 $
证毕
性质2:若$\gcd(a,b)=1$则有$\varphi(ab)=\varphi(a)\varphi(b)$
证明:由定义式即可推导
相似地可引出积性函数的定义
积性函数
当$a,b$互质时,若有$f(ab)=f(a)f(b)$,那么称函数$f$为积性函数
性质
若$f$是积性函数,且在算数基本定理中$n= {\textstyle \prod_{i=1}^{k}p_{i}^{a_i}},$
则$f(n)= {\textstyle \prod_{i=1}^{k}f(p_i^{a_i})} $
证明:把$n$分解质因数这些质因数都互质,按定义显然成立
性质3、 设$p$为质数,若$p\mid{n}$且$p^{2}\mid{n}$,则$\varphi(n)=\varphi(n/p)*p$
证明:$n$与$n/p$含有相同的质因子$p$,所以根据定义,后面那一串噼里啪啦的$(1-\frac{1}{p})$不会用影响,列出式子就能得出性质
性质4、设$p$为质数,若$p\mid{n}$且$p^{2}\nmid{n}$,则$\varphi(n)=\varphi(n/p)*(p-1)$
证明:和性质3差不多,这次说明$p$是唯一质因子,$n/p$后面那一串会少一个$(1-\frac{1}{p})$,
所以有$\frac{\varphi(n)}{\varphi(n/p)}=\frac{1-\frac{1}{p}}{\frac{1}{p}}=p-1$
证毕
性质5、${\textstyle \sum_{d\mid{n}}^{}}\varphi(d)=n$
这下我是真看不懂了,等用到了再说了
Ⅳ、求欧拉函数
给定 $n$个正整数 $a_i$,请你求出每个数的欧拉函数。
原理:欧拉函数定义
板子
除法向下取整,先除分母再乘分子。
#include<iostream>
#include<cstdio>
using namespace std;
int phi(int n)
{
int res=n;
for(int i=2;i<=n/i;i++){
if(n%i==0){
while(n%i==0) n/=i;
res=res/i*(i-1);
}
}
if(n>1) res=res/n*(n-1);
return res;
}
int main()
{
int T;cin>>T;
while(T--){
int n;cin>>n;
cout<<phi(n)<<endl;
}
return 0;
}
Ⅴ、线性筛欧拉函数
给定一个正整数 n,求 $1\sim{n}$ 中每个数的欧拉函数之和。
原理
利用了线性筛和欧拉函数性质$3$与$4$
线性筛的特点是对于每个合数只会用一个最小质因数去筛除。恰好可以利用这一点,首先每个质数的欧拉函数等于自身减一,对于每个合数,如果当前筛除他的是最小质因数,就采用性质$4$递推出他的欧拉函数;如果当前到了不是最小值因数的那个要break掉的地方,就用性质$3$来推,可以做到时间复杂度为$O(n)$
板子
#include<iostream>
using namespace std;
typedef long long ll;
const int N=1e6+10;
ll sumphi(int n)
{
bool st[N]={false};
int phi[N],prime[N],cnt;
phi[1]=1;
for(int i=2;i<=n;i++){
if(!st[i]){
prime[++cnt]=i;
phi[i]=i-1;//素数的欧拉函数
}
for(int j=1;prime[j]<=n/i;j++){
int next=prime[j]*i;
st[next]=true;
if(i%prime[j]==0){//prime[j]已经不是最小质因数了
phi[next]=prime[j]*phi[i];
break;
}
phi[next]=(prime[j]-1)*phi[i];//prime[j]是最小质因数
}
}
ll res=0;
for(int i=1;i<=n;i++) res+=phi[i];
return res;
}
int main()
{
int n;cin>>n;
cout<<sumphi(n)<<endl;
return 0;
}
四、同余
Ⅰ、扩展欧几里得算法$exgcd$
给定 $n$对正整数 $a_i,b_i$,对于每对数,求出一组 $x_i,y_i$,使其满足 $a_i×x_i+b_i×y_i=\gcd(a_i,b_i)$
原理
裴蜀定理+欧几里得算法
对于任意整数$a,b$,存在一对整数$x,y$,满足$ax+by=\gcd(a,b)$。
这个定理的证明和整数$x,y$的计算方法是一起的。
证明:
在欧几里得算法的最后一步,如果$b=0$,显然有$x=1,y=0$使得$ax+by=\gcd(a,0)$
若$b>0$,$\gcd(a,b)=\gcd(b,a\bmod b)$,假设存在$x,y$满足
$bx+(a\bmod b)y=\gcd(b,a\bmod b)=\gcd(a,b)$
$bx+(a-\left\lfloor a/b \right \rfloor *b)y=gcd(b,a\bmod b)=\gcd(a,b)$
$ay+b(x-\left\lfloor a/b \right \rfloor *y)=gcd(b,a\bmod b)=gcd(a,b)$
令$x’=y,y’=x-\left\lfloor a/b \right \rfloor *y$,有$ax’+by’=gcd(a,b)$
因此根据欧几里得算法的递归过程和数学归纳法,裴蜀定理成立。
证毕
求 $x,y$ 的解的过程就是上述递归的过程
先往下递归,回溯时对于每一层有 $x’,y’$
$x’=y,y’=x-\left\lfloor a/b \right \rfloor *y$
板子
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e5+10;
void exgcd(int a,int b,int &x,int &y)
{
if(!b){x=1,y=0;return;}
exgcd(b,a%b,x,y);
int t=x;x=y;y=t-(a/b)*y;
}
int main()
{
int T;cin>>T;
while(T--){
int a,b,x,y;
scanf("%d %d",&a,&b);
exgcd(a,b,x,y);
printf("%d %d\n",x,y);
}
return 0;
}
推广:线性同余方程
给定 $n$ 组数据 $a_i ,b_i,m_i$,对于每组数求出一个 $x_i$,使其满足 $a_i×x_i≡b_i(\bmod m_i)$,如果无解则输出
impossible。
对于更为一般的方程$ax+by=c$,它有解的充分必要条件为$d\mid{c},d=\gcd(a,b)$
因此可以先求解$ax+by=d$的一组特解$(x_0,y_0)$,同时乘上$\frac{c}{d}$就得到了一般方程的特解$(c/d)x_0,(c/d)y_0$
板子
#include<iostream>
using namespace std;
const int N=1e5+10;
int exgcd(int a,int b,int &x,int &y)
{
if(!b){ x=1,y=0;return a;}
int d=exgcd(b,a%b,x,y);
int t=x;x=y;y=t-(a/b)*y;
return d;
}
int main()
{
int T;cin>>T;
while(T--){
int a,b,m,x,y;
scanf("%d%d%d",&a,&b,&m);
int d=exgcd(a,m,x,y);
if(b%d) puts("impossible");
else printf("%d\n",(1ll*x*(b/d))%m);
}
return 0;
}
Ⅱ、乘法逆元
1、定义
若整数 $b,m$ 互质,并且对于任意的整数 $a$,如果满足 $b\mid a$,则存在一个整数 $x$,使得 $a/b≡a*x(mod{m})$,则称 $x$ 为 $b$的模 $m$乘法逆元,记为 $b^{-1}(modm)$。
$b$ 存在乘法逆元的充要条件是 $b$ 与模数 $m$互质。当模数 $m$ 为质数时,$b^{m-2}$ 即为 $b$的乘法逆元。
存在乘法逆元的条件:$b$ 与模数 $m$互质
$a/b≡a\*b^{-1}(mod{m})$,两边同时乘以$b$有
$a\equiv b\*a\*b^{-1}(modm)$
约去$a$,有$b^\*b^{-1}\equiv{1}(modm)$,问题即转化为为求解同余方程
有一个小性质:逆元是积性的,即$(ab)^{-1}=a^{-1}\times b^{-1}$
可以通过同余方程推导
2、模数为质数求乘法逆元
给定 $n$组 $a_i,p_i$,其中 $p_i$是质数,求 $a_i$模 $p_i$ 的乘法逆元,若逆元不存在则输出
impossible。
注意:请返回在 $0∼p−1$之间的逆元。
当模数为质数的时候,可以用快速幂求出乘法逆元
$b^\*b^{-1}\equiv{1}(modm)$
原理:费马小定理
若$p$是质数,则对于任意整数$a$,有$ a^{p}\equiv{a}( \bmod p )$
由费马小定理:$p$是质数,则对于任意整数$a$,有$ a^{p}\equiv{a}( \bmod p )$
因此就找到了一个逆元$b^{-1}=b^{p-2}$
板子(快速幂求乘法逆元)
#include<iostream>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int qmi(int a,int b,int p)
{
int res=1;
while(b){
if(b&1) res=(1ll*res*a)%p;
b>>=1;
a=(1ll*a*a)%p;
}
return res;
}
int main()
{
int T;cin>>T;
while(T--){
int a,p;cin>>a>>p;
if(a%p==0) puts("impossible");//前提:互质
else cout<<qmi(a,p-2,p)<<endl;
}
return 0;
}
3、模数非质数求乘法逆元
原理:扩展欧几里得算法
m不为质数则变为直接求解同余方程:$b^*b^{-1}\equiv{1}(modm)$
有解条件:
- $b$与$m$互质
- $\gcd(b,m)=1$
板子($exgcd$求乘法逆元)
#include<iostream>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int exgcd(int a,int b,int &x,int &y)
{
if(!b) {x=1,y=0;return a;}
int d=exgcd(b,a%b,x,y);
int t=x;x=y;y=t-(a/b)*x;
return d;
}
int main()
{
int T;cin>>T;
while(T--){
int a,p;scanf("%d%d",&a,&p);
int x,y;
if(a%p==0) puts("impossible");
else{
int d=exgcd(a,p,x,y);
if(d!=1) puts("impossible");
else printf("%d\n",((1ll*x)%p+p)%p);
}
}
return 0;
}
Ⅲ、中国剩余定理
我暂时不会↑
五、组合计数
Ⅰ、定义
从$n$个不同元素中依次取出$m$个组成一个集合(不考虑顺序),产生的不同集合数量为:
$C_{n}^{m} =\frac{n!}{m!(n-m)!}=\frac{n\*(n-1)\*\cdots\*(n-m+1) }{m\*(m-1)\*\cdots\*2\*1}$
这个式子是由排列数除以 $m!$ 也就是去除重复的部分得到的,$m$个元素的排列有 $m!$ 种
Ⅱ、性质
1、$C_{n}^{m}=C_{n}^{n-m}$
证明:选出的集合与剩余部分组成的集合一一对应,所以数量也相等
2、$C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}$
证明:类似$01$背包,对于第$m$个物品选或不选,所有的状态可以由后两者转移过来
3、 $C_{n}^{0}+C_{n}^{1}+\cdots+C_{n}^{n}=2^n$
证明:任意的挑物品就等价于每个物品选或不选,有$2^n$种选法。
Ⅲ、组合数的求法
给定 $n$ 组询问,每组询问给定两个整数 $a,b$ ,请你输出 $C_{a}^{b}\bmod(1e9+7) $的值。
1、递推 $O(n^2)$
数据范围
$1≤n≤10000$
$1≤b≤a≤2000$
原理:性质 $2$
根据性质 $2$ : $C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}$ 可以递推求出所有的组合数
板子
#include<iostream>
#include<cstdio>
using namespace std;
const int N=2010,mod=1e9+7;
int C[N][N];
void init()
{
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++)
if(!j) C[i][j]=1;//选0个
else C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
int main()
{
init();
int T;cin>>T;
while(T--){
int a,b;cin>>a>>b;
cout<<C[a][b]<<endl;
}
return 0;
}
2、逆元 $O(nlogn)$
数据范围
$1≤ n ≤10000$
$1≤ b ≤ a ≤10^5$
原理:费马小定理
由定义:$C_{n}^{m} =\frac{n!}{m!(n-m)!}$
可以直接预处理出来两个数组: $fact[i]$代表 $i$ 的阶乘$\bmod{p}$,$infact[i]$ 代表 $i$ 的阶乘的逆元$ \bmod{p} $
因为 $p$ 为一个质数,由费马小定理 $a^p\equiv a(\bmod p)$,$a$ 的逆元为 $a^{p-2}$
可以用$O(nlogn)$的时间递推出 $infact[i]$
板子
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=1e9+7;
int fact[N],infact[N];
int qmi(int a,int b,int p)
{
int res=1;
while(b){
if(b&1) res=((ll)res*a)%p;
b>>=1;
a=(ll)a*a%p;
}
return res;
}
void init()
{
fact[0]=1,infact[0]=1;
for(int i=1;i<N;i++){
fact[i]=((ll)fact[i-1]*i)%mod;
infact[i]=((ll)infact[i-1]*qmi(i,mod-2,mod))%mod;//积性递推
}
}
int main()
{
init();
int T;cin>>T;
while(T--){
int a,b;scanf("%d%d",&a,&b);
printf("%d\n",((ll)fact[a]*infact[b]%mod)*infact[a-b]%mod);//三个数记得先mod一次
}
return 0;
}
3、$Lucas$定理$O(log_pn\times plogp)$
数据范围
$1≤ n ≤20$,
$1≤ b ≤ a ≤10^{18},$
$1≤ p ≤10^5,$
原理:$Lucas$定理
若 $p$ 是质数,对于任意整数 $1\le{m}\le{n}$ ,有:
$C_{N}^{M}\equiv C_{N\bmod{p}}^{M\bmod{p}}\times{C_{N/p}^{M/p}}(\bmod{p})$
证明:我不会
板子
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
int qmi(ll a,ll b,int p)
{
ll res=1;
while(b){
if(b&1) res=res*a%p;
b>>=1;
a=(ll)a*a%p;
}
return res;
}
int C(ll a,ll b,int p)
{
int res=1;
for(int i=a,j=1;j<=b;j++,i--){
res=(ll)res*i%p;
res=(ll)res*qmi(j,p-2,p)%p;
}
return res;
}
int lucas(ll a,ll b,int p)
{
if(a<p&&b<p) return C(a,b,p);
return (ll)C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main()
{
int T;cin>>T;
while(T--){
ll a,b;
int p;
scanf("%lld%lld%d",&a,&b,&p);
printf("%d\n",lucas(a,b,p));
}
return 0;
}
4、高精度$(nlogn)$
高精度一律放弃
数据范围
$1≤ b ≤ a ≤5000$
原理:阶乘分解素数
参考:阶乘分解
根据定义 $C_{n}^{m} =\frac{n!}{m!(n-m)!}$ ,如果直接算的话要实现一个高精度除法,很麻烦
可以考虑把$C_{n}^{m} $分解质因数成 $p_1^{a_1}\times\cdots \times p_k^{a_k}$ 的形式
阶乘分解质因数可以参考:阶乘分解 这个题,然后上下算出每个素数的幂直接相减就可以了,最后只需要高精度乘法。
时间复杂度 $O(nlogn)$
板子
#include<iostream>
#include<vector>
using namespace std;
const int N=5010;
vector<int> ans;
int sum[N];
int primes[N],cnt;
bool st[N];
vector<int> times(vector<int> &a,int b)
{
vector<int> c;
int t=0;
for(int i=0;i<a.size();i++){
t+=a[i]*b;
c.push_back(t%10);
t/=10;
}
while(t){
c.push_back(t%10);
t/=10;
}
return c;
}
void get_primes(int n)//筛素数
{
for(int i=2;i<=n;i++){
if(!st[i]) primes[++cnt]=i;
for(int j=1;primes[j]<=n/i;j++){
st[primes[j]*i]=true;
if(i%primes[j]==0) break;
}
}
}
int count(int p,int n)//n!能分解成多少个p
{
int sum=0;
while(n){
sum+=n/p;
n/=p;
}
return sum;
}
int main()
{
int a,b;cin>>a>>b;
get_primes(a);
for(int i=1;i<=cnt;i++){
int p=primes[i];
sum[i]=count(p,a)-count(p,b)-count(p,a-b);
}
ans.push_back(1);
for(int i=1;i<=cnt;i++){
int p=primes[i];
for(int j=1;j<=sum[i];j++) ans=times(ans,p);
}
for(int i=ans.size()-1;i>=0;i--) cout<<ans[i];
puts("");
return 0;
}
Ⅳ、$Catalan$数列
给定 $n$ 个 $0$ 和 $n$ 个 $ 1$ ,它们按照某种顺序排成长度为 $2n$ 的序列,满足任意前缀中 $0$ 的个数都不少于 $1$ 的个数的序列数量为:
$Cat_n=\frac{C_{2n}^{n}}{n+1}$
证明:把 $01$ 序列放到二维坐标系里面转化成路径
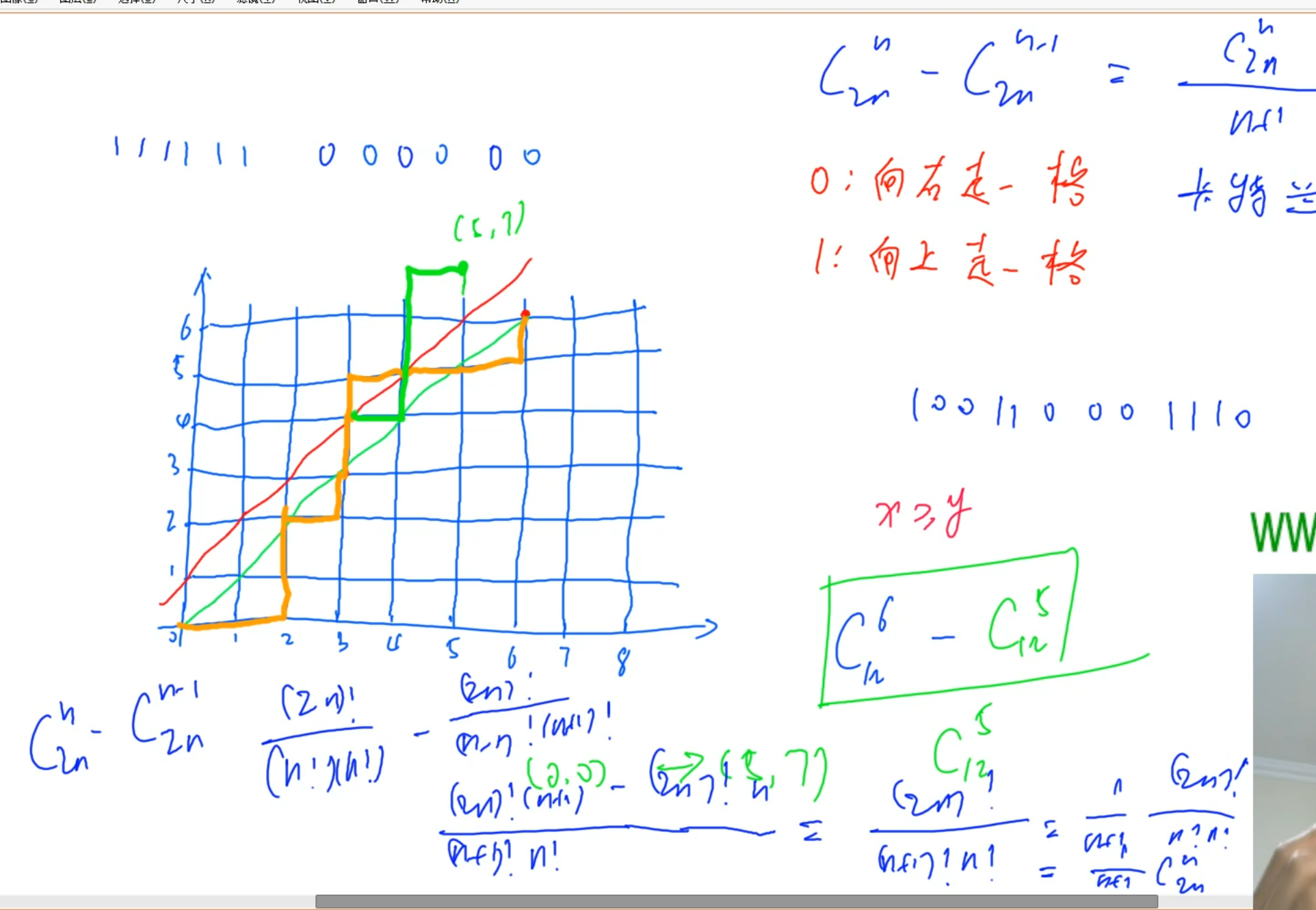
所有的走法等于$C_{2n}^{n}$
对于所有不合法的方案路径必定会碰到红色的线,那么对所有这些不合法路径对红色线对称翻折,一定会不重不漏一一对应到达终点 $(n,n) $关于红色线的对称点 $(n-1,n+1)$。
因此不合法的方案数就等于到达 $(n-1,n+1)$ 的方案数:$C_{2n}^{n-1}$
$Cat_n=C_{2n}^{n}-C_{2n}^{n-1}=\frac{C_{2n}^{n}}{n+1}$
板子
快速幂求逆元,方法与求组合数 $2$ 一样。
#include<iostream>
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=1e9+7;
int qmi(int a,int b,int p)
{
ll res=1;
while(b){
if(b&1) res=res*a%p;
b>>=1;
a=1ll*a*a%p;
}
return res;
}
int main()
{
int n;cin>>n;
int a=n*2,b=n;
ll res=1;
for(int i=a,j=1;j<=b;i--,j++) res=res*i%mod;
for(int i=1;i<=b;i++) res=res*qmi(i,mod-2,mod)%mod;
res=res*qmi(n+1,mod-2,mod)%mod;
cout<<res<<endl;
return 0;
}
六、容斥原理
剩下的章节暂时不打算学了
哈哈

