字典树 ( Trie 树 ) 详解
一、字典树 ( Trie 树 ) 简介
字典树 ( Trie 树 ) 又称单词查找树,
是一种用于在 字符串集合 中 高效地 存储 和 查找 字符串 的 树形 数据结构。
二、应用场景
维护一个 字符串集合 ,并支持两种操作:
- 向集合中插入一个字符串
xx; - 询问一个字符串
xx在集合中出现了多少次。
例如:有字符串集合
{ “abc” , "acwing" , "hhhh"}
1. 插入字符串“abc”==> 集合{ “abc” , “abc” , "acwing" , "hhhh"}
2. 查询字符串“abc”出现的次数:2 次。
三、Trie 树举例
原字符串集合:{ abcde 、aced 、bcdf 、bcff }
插入字符串:aced 、cdaa
新字符串集合:{ abcde 、abde、aced 、bcdf 、bcff 、cdaa }
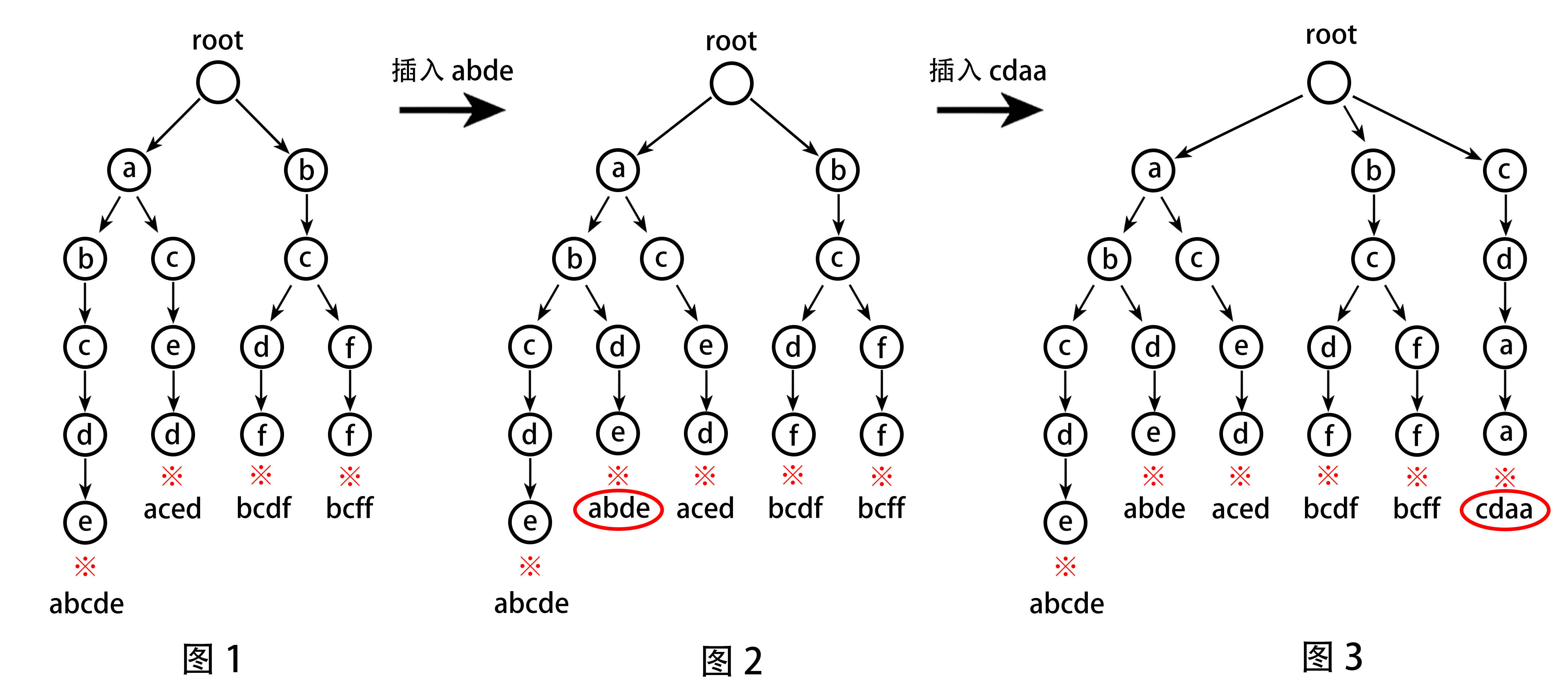
说明:图中 ※ 为 字符串结束的标记 。
若某结点上有标记 ※,则说明 从根结点 到该结点为止,
每个结点表示的字符 相连 组成的字符串存在于集合中。
相应的,对于 没有标记 的结点,
串联成的字符串只是原有字符串的 一部分 ,不属于 字符串集合。
四、操作原理解析:
1. 插入 ( insert ) 操作
将字符串 逐个拆分 成 单个字符,
从第一个字符开始与 Trie 树的 根结点开始 的 子结点 比对,
若有结点具有 相同 的字符,
则以同样的方式对比 下一个字符 与该结点的 子结点 。
举例:在 图 1 中插入字符串
abde( 拆分:a/b/d/e)
对于字符a,根结点 的 子结点 中有a,向后判断 下一个字符b与 结点a的 子结点;
对于字符b,a结点的 子结点 中有b,向后判断下一个字符d与 结点b的子结点;
对于字符d,b结点的子结点中 没有d,
因此要创建新结点d,向后 判断下一个字符e与 结点d的 子结点;
对于字符e,d结点的子结点中没有e,因此要创建新结点e
( 从创建了一个新结点起,后面剩下的字符显然都要创建新的结点,但其 操作和之前的判断相同 )
举例:在 图 2 中插入字符串
cdaa( 拆分:c/d/a/a)
对于字符c,根结点的子结点中没有c,因此要创建新结点c,
剩下的字符daa以相同的操作,逐个创建,以存储字符串。
注意:在插入完字符串之后,要给末尾的结点加上 结束标记。
2. 查询 ( query ) 操作
与插入操作的原理基本相同,
将需要查询的字符串 逐个拆分 成单个字符,逐个与 Trie 树中的结点比较,
直至发现 Trie 树中 不存在 的字符,或要查询的字符串的各个字符都 比较完成 。
对于发现 Trie 树中不存在的字符,
一旦发现,就能确定要查询的字符串不属于原集合。
举例:在图 3 中查询
acwing,
能找到a → c,但c的子结点中没有w,则确定集合中不存在该字符串 )
对于要查询的字符串的各个字符都比较完成,则存在两种情况:
① 要查询的字符的确属于集合;
② 要查询的字符是集合中某个字符串的前缀。
举例:在图 3 中查询
ac,能找到a → c,字符串比较完成。
因为ac是原有字符串aced的一部分 ( 前缀 )。
此时就需要用到结点上的 字符串结束标记 了。
在
ac的查询过程中,最后判断的结点落在了结点c上,
但该结点没有 字符串结束标记 ,因此可以判断ac不属于原集合。举例:在图 3 中查询
aced,最后判断的结点落在了结点d上,
该结点具有 字符串结束标记 ,因此可以判断aced属于原集合。
五、数组模拟实现 Trie 树
1. Trie 树的定义
int son[N][26]; // 存储每个结点的所有儿子结点
// 在题目中,字符串只包含 26 个小写字母
// 因此每个结点最多只会向外连 26 条边 ( 最多只有 26 个儿子结点 )
int cnt[N]; // count,记录以这个结点结尾的单词有多少个
// 它在本模板中作为 字符串结束标记
int idx; // 存储当前已经使用到的结点的下标
// 下标是 0 的结点,既是根节点,又是空结点
char str[N]; // 存储输入的字符串
( 1 ) 对二维数组的理解:
一维数组 array[x],表示以 array 为名的数组,
其中有 x 个元素,对应下标 0/1/2/.../x-1
对于二维数组,例如上述的 son[N][26] ,表示以 son 为名的数组,
其中共有 N * 26 个元素。
对于第一个下标 0 ,有
son[0][0]son[0][1]son[0][2]…son[0][25]共 26 个元素
对于第一个下标 1 ,有son[1][0]son[1][1]son[1][2]…son[1][25]共 26 个元素
......
因此可以把 son[N][26] 看成 由 N 个数组组成,每个数组有 26 个元素。
即 将 son[N] 看作数组名,而其下标 N ,可以作为数组的编号。
回到 Trie 树,我们将这 N 个数组看作 N 个 结点 。
下标是 0 的结点
son[0],既是根节点root,又是空结点。
( 2 ) 对二维数组中 26 的理解
一个结点,它包含了 26 个元素,对应 26 个小写字母。
( 0 - a / 1 - b / 2 - c / ... / 25 - z)
这些元素的初始值均为 0 ,表示该结点没有指向任何一个字母的边。
若值不等于零,则表示有指向对应字母的边。
当然,若值不等于零,也就能判断该字符串属于集合。
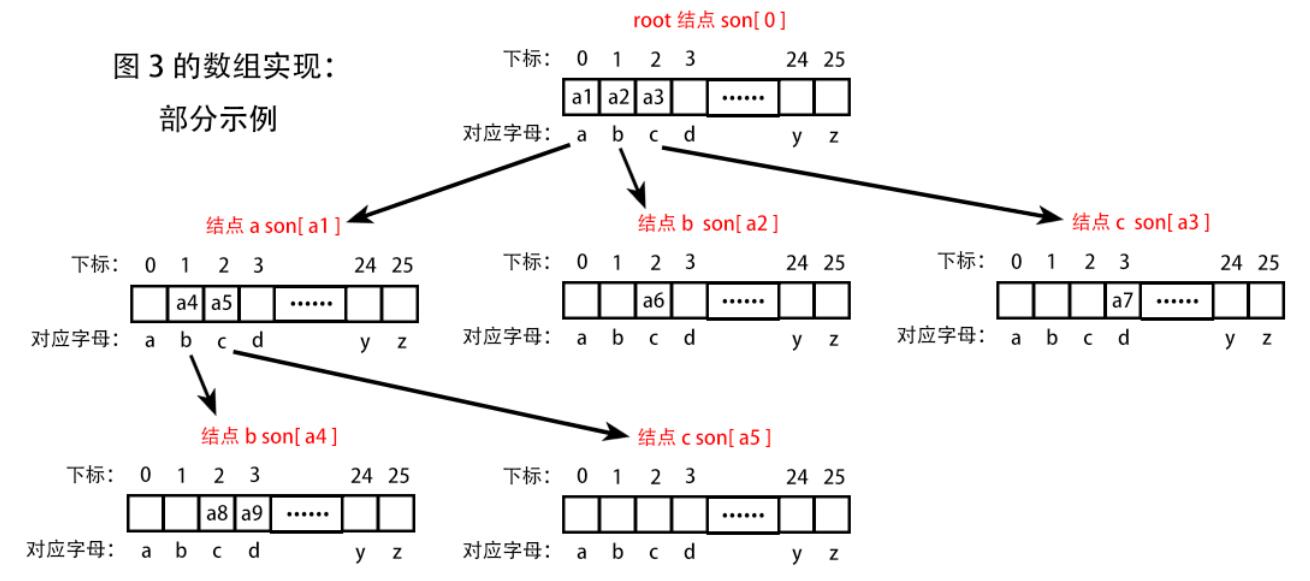
例如 图 3 中
son[0][0] (a)son[0][1] (b)son[0][2] (c)的值均不为0
说明从根结点 (root)son[0]出发,有到abc的边。
而这个值,就是指向的 结点的编号。
son[0][0] = x,则指向的结点a为son[x]
结点a指向结点b —— son[x][1] = y,c —— son[x][2] = z
则结点b为son[y],结点c为son[z]
2. 插入 ( insert ) 操作
void insert( char str[] )
{
int p = 0; // 每次都从根结点出发
for( int i = 0; str[i]; i++ ) // c++ 字符串结尾是 \0,可用于遍历整个字符串
{
int u = str[i] - 'a'; // 得到当前字母子结点编号
if( !son[p][u] ) son[p][u] = ++ idx; // 如果该子结点不存在,创建子结点
p = son[p][u]; // 进入该子结点
}
// 上面的 for 循环结束,则要插入的字符串遍历结束
// 此时 p 对应的就是最后一个字符所在的结点
cnt[p] ++; // 在末尾的结点处增加 结束标记 ( 该字符串出现的次数的累加 )
}
3. 查询 ( query ) 操作
int query( char str[] ) // 返回该字符串出现过多少次
{
int p = 0; // 每次都从根结点出发
for( int i = 0; str[i]; i++) // c++ 字符串结尾是 \0,可用于遍历整个字符串
{
int u = str[i] - 'a'; // 得到当前字母子结点编号
if( !son[p][u] ) return 0; // 发现不存在的字符,则断定不存在该单词,return 0
p = son[p][u]; // 存在则进入该子结点
}
// 上述 for 循环结束,查询的字符串遍历结束
return cnt[p]; // 返回以 p 结尾的单词数量
// 若该结点没有 结束标记 则会返回 0
}
说明:cnt[N] 作为字符串结束标记,其值默认初始值均为 0
若 cnt[p] == x != 0 则说明结点 p 具有结束标记。(其值 x 表示字符串的数量)
六、函数模板
#include <iostream>
using namespace std;
const int N = 100010;
int son[N][26]; // 存储每个结点的所有儿子结点
// 在题目中,字符串只包含 26 个小写字母
// 因此每个结点最多只会向外连 26 条边 ( 最多只有 26 个儿子结点 )
int cnt[N]; // count,记录以这个结点结尾的单词有多少个
// 它在本模板中作为 字符串结束标记
int idx; // 存储当前已经使用到的结点的下标
// 下标是 0 的结点,既是根节点,又是空结点
char str[N]; // 存储输入的字符串
void insert( char str[] )
{
int p = 0; // 每次都从根结点出发
for( int i = 0; str[i]; i++ ) // c++ 字符串结尾是 \0,可用于遍历整个字符串
{
int u = str[i] - 'a'; // 得到当前字母子结点编号
if( !son[p][u] ) son[p][u] = ++ idx; // 如果该子结点不存在,创建子结点
p = son[p][u]; // 进入该子结点
}
// 上面的 for 循环结束,则要插入的字符串遍历结束
// 此时 p 对应的就是最后一个字符所在的结点
cnt[p] ++; // 在末尾的结点处增加 结束标记 ( 该字符串出现的次数的累加 )
}
int query( char str[] ) // 返回该字符串出现过多少次
{
int p = 0; // 每次都从根结点出发
for( int i = 0; str[i]; i++) // c++ 字符串结尾是 \0,可用于遍历整个字符串
{
int u = str[i] - 'a'; // 得到当前字母子结点编号
if( !son[p][u] ) return 0; // 发现不存在的字符,则断定不存在该单词,return 0
p = son[p][u]; // 存在则进入该子结点
}
// 上述 for 循环结束,查询的字符串遍历结束
return cnt[p]; // 返回以 p 结尾的单词数量
// 若该结点没有 结束标记 则会返回 0
}
int main()
{
int n;
scanf( "%d", &n );
while( n-- )
{
char op[2]; // 用于输入一个字符,
scanf( "%s%s", op, str );
if( op[0] == 'I' ) insert(str);
else printf( "%d\n", query(str) ); // op[0] == 'Q'
}
return 0;
}
说明:代码中的 char op[2] 是一种输入单个字符的技巧
函数
scanf对于char类型的单个字符,是可以输入 空格 、回车 等字符的。
在代码的 提交测试过程 中,我们不确定输入的字符之后是否会有空格,
而这类错误是我们无法解决的。而用
scanf读入字符串能忽略掉 空格 和 回车,
采用这种方式,此时的op[0]便是所输入的字符。
七、补充
1. Trie 树 基本性质:
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符;
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串;
- 每个节点的所有子节点包含的字符都不相同。
2. Trie 树的优缺点
Trie 树是一种 以空间换时间 的数据结构。
优点:利用字符串的 公共前缀 来减少查询时间,最大限度地减少无谓的字符串比较。
公共前缀:例如字符串
abcdef与abcghi有公共前缀abc。
缺点:其每一个字符都可能包含至多字符集大小数目的指针。
在本模板采用子结点默认包含 所有字符集 的连接方式,
对于少量的字符串存储来说,大量的结点的儿子是空闲的,造成了 空间的浪费 。
3. 何时使用 Trie 树
当需要存储的字符串的字符种类有限 ( 较少 ) 时,
可以用 Trie 树来存储字符串。
例如:只包含小写字母 ( 26 个 ),或包含大小字母 ( 52 个 ),
或包含 0 / 1,或包含整数
八、参考资料
九、( 无注释版 ) 函数模板
#include <iostream>
using namespace std;
const int N = 100010;
int son[N][26], idx, cnt[N];
char str[N];
void insert( char str[] )
{
int p = 0;
for( int i = 0; str[i]; i++ )
{
int u = str[i] - 'a';
while( !son[p][u] ) son[p][u] = ++idx;
p = son[p][u];
}
cnt[p]++;
}
int query( char str[] )
{
int p = 0;
for( int i = 0; str[i]; i++ )
{
int u = str[i] - 'a';
while( !son[p][u] ) return 0;
p = son[p][u];
}
return cnt[p];
}
int main()
{
int n;
scanf( "%d", &n );
while( n-- )
{
char op[2];
scanf( "%s%s", op, str );
if( op[0] == 'I' ) insert( str );
else if( op[0] == 'Q' ) printf( "%d\n", query( str ));
}
return 0;
}
(接受批评指正,欢迎交流补充~~ XD)


从另一题的题解来的,太厉害啦
牛
谢啦
很详细hh
谢谢~hh