模拟哈希表
一、哈希表简介：
哈希表 ( 也称为散列表 ) 是一种具有特殊的数据 存储 和 查找 方式的 数组 。
-
对于将要 存储 的数据
x，哈希表通过一种 映射关系 ( 哈希函数f(x)) ，
计算出 该数据在数组中的 下标k = f(x)，将其保存h[ k ] = x -
若要 查找 数据
x是否在哈希表中，就能通过同样的哈希函数，
直接计算 出其对应的下标k = f(x)，判断h[k]存储的是否是该元素。
相比于一般的数组，哈希表中元素的查找能 免去大量的比较操作 。
类比一般的一维数组：
一维数组 会随着 下标 的递增，顺序 地存储数据。
若要判断某个数据是否属于该数组，
则需从第一个数组元素开始，逐个比较，以判断是否存在该元素。
二、应用场景
维护一个集合，支持如下几种操作：
- 插入一个数 x ；
- 询问数 x 是否在集合中出现过；
三、哈希表的核心 —— 哈希函数
哈希表通过 哈希函数 ，可以将一个 大范围 的数据，映射到一个 较小的范围 。
说明：
哈希函数 将每个数据对应到数组中的一个 下标 ，
使得 查找元素 操作的时间复杂度接近 O(1) 。
但相应的，我们需要为每个元素提供其 对应的 存储空间。
又因为静态数组的大小从一开始就固定，因此若数据元素与下标 一 一对应，
且数据可能的范围很大，则初始时就需要开辟很大的数组。
例如：要存储的数据 10^(-9) < x < 10 ^ 9，则需要开辟大小为 2 * 10^9 的数组。
但大多数情况下，虽然数据的范围很大，但是数据的 数量很少 ，
以举例中的方式存储，则会有很多的 空间浪费 。
因此我们就需要合理设计哈希函数，
将大范围的数据映射到一个较小的区间，
这样既能快速查找，又能有效利用空间。
例如：有 5 个数据，对于任意的数据 x ∈ ( 10^(-9) , 10^9 )
则只需要开辟大小 至少 为 5 的数组，就能全部存储了。
四、哈希函数的设计
实际工作中需视不同的情况采用不同的哈希函数。
在本模板中，我们使用简单的 取余操作 ( mod / % ) 作为哈希函数。
说明：
对于任意大小的数 x，设定区间大小 N，则 x mod N ∈ [ 0, N - 1 ] 。
由此便将大范围的数 x ，映射到小范围 [ 0, N - 1 ] 中 。
{:height=”70%” width=”70%”}
举例：哈希表
h[N]，大小N = 10，哈希函数f(x) = x % 10存储数据
x = 62，
下标k = f(x) = 62 % 10 = 2，因此h[k] = h[2] = 62查询数据
x = 16是否存在：
下标k = f(x) = 16 % 10 = 6，h[k] = h[6] == 16查询成功查询数据
x = 71是否存在：
下标k = f(x) = 71 % 10 = 1，h[k] = h[1] == null，不存在该数据。
对取模运算中模数的要求
在使用哈希表时，取模运算中的模数一般要取质数，
而且这个质数要离 2 的整数次幂尽可能远。
这么取发生冲突的概率最小。( 可通过数学方法证明 )
五、冲突的处理
哈希函数作为一种映射关系，可能将不同的数映射到了同一个位置，发生冲突 。
冲突举例：哈希表同上，现在要存储数据
x = 84
下标k = f(x) = 84 % 10 = 4，按照规定应该存储h[k] = h[4] = 84，
但是原哈希表中，h[4] = 34，已经存在元素，发生冲突 。
{:height=”70%” width=”70%”}
因此需要额外处理发生冲突的情况。
根据处理冲突的方式不同，将构建哈希表的方法分为：
- 拉链法；
- 开放寻址法。
六、拉链法 构建哈希表
哈希函数可能将多个不同的数值映射到同一个位置，
若该位置只能存储一个数，则会发生冲突。
拉链法则使得该位置能存储多个数，而要想存下所有数，
可以在每个位置设置一个单链表，来存储这个位置当前有的所有数。
此时哈希表中的数值便是单链表的头结点 Head 。
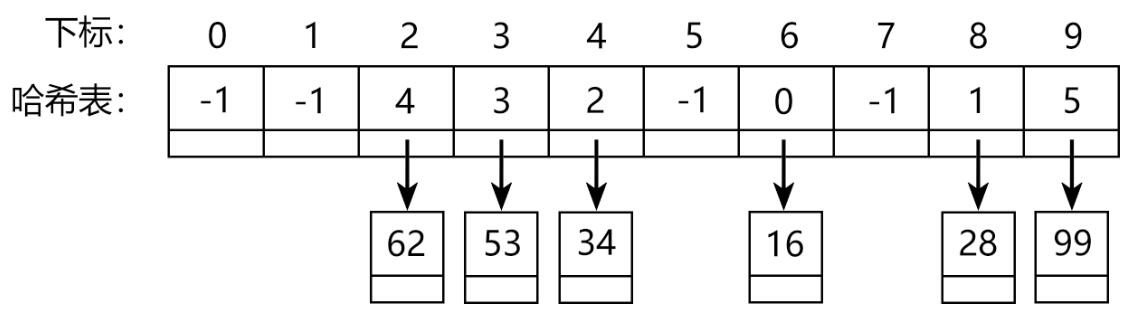{:height=”70%” width=”70%”}
现在要存储数据 x = 84 ，下标 k = f(x) = 84 % 10 = 4 ，
因此在哈希表中下标为 4 的单链表中插入新元素 x = 84
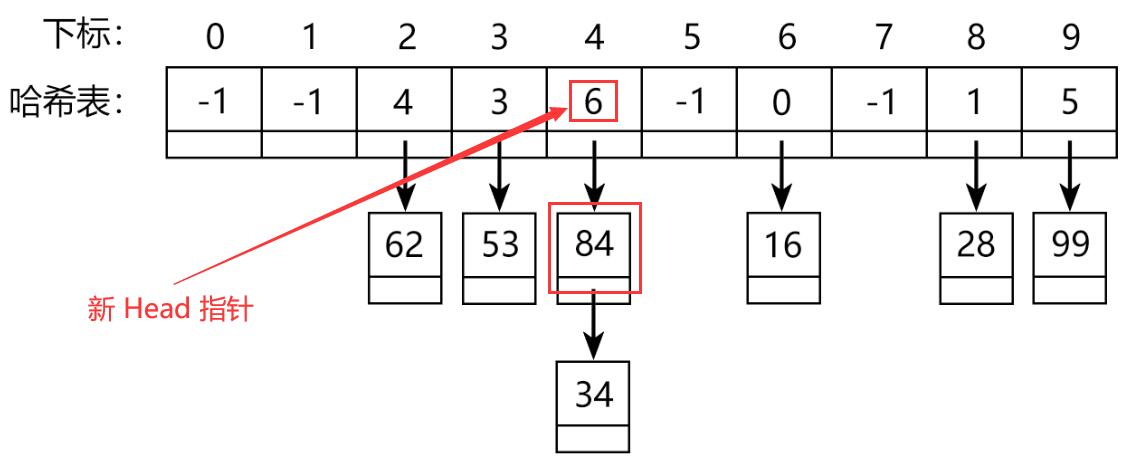{:height=”70%” width=”70%”}
七、代码实现 —— 拉链法
1. 哈希表的定义
const int N = 100003; // 100003 是大于 10万 的第一个质数
int h[N]; // 哈希表 ( 每个单链表的头结点 Head ) 初始值为 -1
int e[N]; // 单链表结点的值
int ne[N]; // 单链表结点的 next 指针
int idx; // idx 递增，作为单链表结点的下标
说明：重温单链表：数组模拟实现单链表 - AcWing
2. 插入 ( insert ) 操作
void insert( int x ) // x 为要插入的数
{
// 哈希函数，将 x 映射到 0 ~ N
int k = ( x % N + N ) % N;
// + N % N 目的是为了让 k 变为 正数
// 在 C ++ 中，对于取模运算 % ， 正数取模为整数，负数取模为负数
// k 为哈希值，即每个数 对应的 存储位置
// 单链表的插入操作
// 这里 h[k] 相当于头指针 head，因此数据插入到链表开头
e[idx] = x;
ne[idx] = h[k];
h[k] = idx;
idx ++;
}
说明：
哈希函数：f(x) = ( x % N + N ) % N
对于 正数 x ，就是简单的取模运算，后面的 + N 后再 % N 对结果无影响。
但对于 负数 x ，若单纯 f(x) = x % N ，
在 C ++ 中结果为负，无法作为数组的下标 ，因此需要将其 转换为正数。
这里可能会有疑问：+N 再 %N 之后结果 不等于 取模运算了，
但这样处理并没有影响，
只要让一个数据 x 在经过哈希函数计算后能对应到一个唯一的下标，
我们就能查询到这个数。
对于向哈希表中插入重复的元素，具体的要求可以在程序进行判断处理。
3. 查询 ( find ) 操作
bool find( int x ) // x 为要查询的数
{
// 以同样的哈希函数，计算出 x 对应的下标 k
int k = ( x % N + N ) % N;
for( int i = h[k]; i != -1; i = ne[i] ) // 单链表中按照 next 指针 寻找 x
if( e[i] == x ) return true;
return false; // 哈希表中不存在 元素 x
}
注意：
- 哈希表中存储的是 head 指针，默认值是
-1，
因此将i != -1作为循环结束条件 - 注意循环中
i的变化，是i = ne[i]指向下一个结点，而不是i++
八、函数模板 —— 拉链法
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100003; // 100003 是大于 10万 的第一个质数
int h[N]; // 哈希表 ( 每个单链表的头结点 Head )
int e[N]; // 单链表结点的值
int ne[N]; // 单链表结点的 next 指针
int idx; // idx 递增，作为单链表结点的下标
void insert( int x ) // x 为要插入的数
{
// 哈希函数，将 x 映射到 0 ~ N
int k = ( x % N + N ) % N;
// + N % N 目的是为了让 k 变为 正数
// 在 C ++ 中，对于取模运算 % ， 正数取模为整数，负数取模为负数
// k 为哈希值，即每个数 对应的 存储位置
// 单链表的插入操作
// 这里 h[k] 相当于头指针 head，因此数据插入到链表开头
e[idx] = x;
ne[idx] = h[k];
h[k] = idx;
idx ++;
}
bool find( int x ) // x 为要查询的数
{
// 以同样的哈希函数，计算出 x 对应的下标 k
int k = ( x % N + N ) % N;
for( int i = h[k]; i != -1; i = ne[i] ) // 单链表中按照 next 指针 寻找 x
if( e[i] == x ) return true;
return false; // 哈希表中不存在 元素 x
}
int main()
{
int n ;
scanf( "%d", &n );
// 将哈希表中所有元素初始化为 -1，作为 head 指针
memset( h, -1, sizeof h );
while( n-- )
{
char op[2];
int x;
scanf( "%s%d", op, &x );
if( op[0] == 'I' ) insert(x);
else // op[0] == 'Q'
{
if( find(x) ) puts( "Yes" );
else puts( "No" );
}
}
return 0;
}
九、开放寻址法 构建哈希表
开放寻址法 不用单链表 存储冲突的数据，
而是为冲突的数据寻找 其他空闲的位置 ，用于存储。
因此哈希表中存储的不再是指针 ( 下标 ) ，而是具体的数值。
插入数据 x 时，哈希函数同上，但在发生冲突时，
我们再向后移动一位，看看是否为空，
若仍已经被其他数据占用，则继续向后移动，直到找到空闲位置，存储数据。
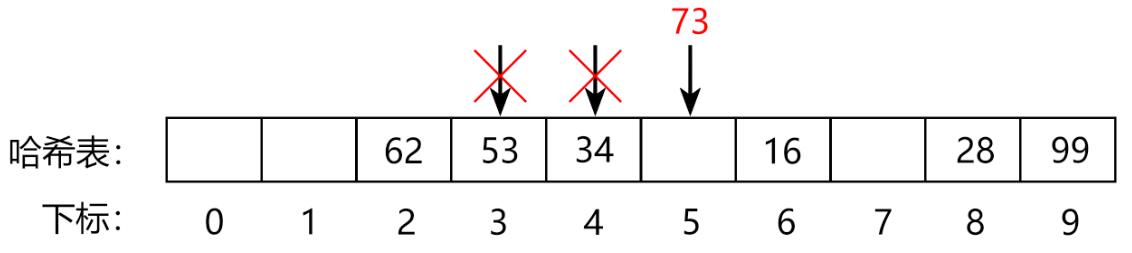
举例：存储数据
x = 73，下标k = f(x) = 73 % 10 = 3
但此时h[3] = 53，所以下标 k 向后移动k++ == 4
但此时h[4] = 34，所以下标 k 向后移动k++ == 5
此时h[5]为空，因此将 73 存入h[5]
若向后移动到了数组的末尾 h[N-1] 还没有空闲位置，
则返回数组的开头搜索 k = 0
{:height=”70%” width=”70%”}
存在的问题：倘若哈希表的整个数组都被占用了，
这样再插入新的元素，则会陷入死循环。
因此从经验上看，构成哈希表的数组要开到 题目所需的两到三倍 。
( 位置比插入的数据个数要多，这样就一定能找到合适的位置，也就不会陷入死循环)
查找数据 x 时，用哈希函数计算出对应位置 ( 下标 )，
如果该位置没有元素 ( null ) ，则判断不存在；
如果有元素，但不是要找的那个，则向后寻找，直到找到或遇到 null 。
十、代码实现 —— 开放寻址法
1. 哈希表的定义
const int N = 200003; // 100003 是大于 20万 的第一个质数
const int null = 0x3f3f3f3f;
// null 的取值只要比 N 大就行，在下标与数据的范围之外
int h[N]; // 哈希表 ( 存储具体的数值 )
2. 查找 ( find ) 操作
int find( int x )
{
int k = ( x % N + N ) % N; // 哈希函数，将 x 映射到 0 ~ N
while( h[k] != x && h[k] != null )
{
k++;
if( k == N ) k = 0; // 如果从最初的 k 到结尾都看完了，返回第一个位置
}
return k;
}
说明：数据的插入和查询都通过 find 函数实现。
若哈希表中存在数据 x ，则返回 x 的位置；
若不存在 x ，返回 x 的应该存储的位置。
十一、函数模板 —— 开放寻址法
#include <iostream>
#include <cstring>
using namespace std;
const int N = 200003; // 200003 是大于 20万 的第一个质数
const int null = 0x3f3f3f3f;
// null 的取值只要比 N 大就行，在下标与数据的范围之外
int h[N]; // 哈希表 ( 存储具体的数值 )
// 如果 x 存在的话，则返回 x 的位置
// 如果 x 不存在的话，返回 x 的应该存储的位置
int find( int x )
{
int k = ( x % N + N ) % N; // 哈希函数，将 x 映射到 0 ~ N
while( h[k] != x && h[k] != null )
{
k++;
if( k == N ) k = 0; // 如果从最初的 k 到结尾都看完了，返回第一个位置
}
return k;
}
int main()
{
memset( h, 0x3f, sizeof h );
// memset 按字节赋值，h 是一个 int 型的数组，每个元素有 4 个字节
// 每个字节都是 0x3f，所以每个数为 0x3f3f3f3f
int n;
scanf( "%d", &n );
while( n-- )
{
char op[2];
int x;
scanf( "%s%d", op, &x );
int k = find(x);
if( op[0] == 'I' )
{
h[k] = x;
}
else
{
if( h[k] != null ) puts("Yes");
else puts("No");
}
}
return 0;
}
说明：
函数 memset 按字节赋值，
而 h 是一个 int 型的数组，每个元素有 4 个字节，
每个字节都是 0x3f，所以每个数组元素值为 0x3f3f3f3f
另外例如：
memset( h, 0, sizeof h );
0 的每个字节都是 0 ，所以四个字节都是 0，整体的值也就是 0
memset( h, -1, sizeof h );
-1 的每个字节都是 1 ，所以四个字节都是 1，整体的值也就是 -1
十二、补充
- 在拉链法构建哈希表中，在平均情况看，每一条连的长度可以看作一个常数，
一般情况下哈希表查询的时间复杂度可以看作 O(1)； - 算法题中，哈希表一般只有添加和查找两种操作，很少有删除操作。
十三、参考资料
（接受批评指正，欢迎交流补充~~ XD）
tql