算法基础课完结撒花！！！

时空复杂度分析

直接参考这篇笔记： https://www.acwing.com/blog/content/3398/

一般ACM或者笔试题的时间限制是 1 秒或 2 秒

C++ 一般1s能计算 10^7 ~ 10^8 次，在这种情况下，C++代码中的操作次数控制在 10^7为最佳

不同数据范围下代码的时间复杂度和算法的选择技巧：

• n ≤ 30，指数级别
  dfs+剪枝
  状态压缩dp

• n ≤ 100，O(n^3)
  floyd
  dp

• n ≤ 1000，O(n^2)，O(n^2*logn)
  dp
  二分
  朴素版Dijkstra
  朴素版Prim
  Bellman - Ford

• n≤10000，O(n√n)
  块状链表
  分块
  莫队

• n ≤ 10^5，O(nlogn)
  各种排序算法
  线段树
  树状数组
  set/map
  heap
  拓扑排序
  堆优化Dijkstra
  堆优化Prim
  SPFA
  求凸包
  求半平面交
  二分

• n ≤ 10^6
  O(n)
  Hash
  双指针扫描
  并查集（O(nlogn)） find函数是O(logn)
  KMP
  AC自动机
  常数较小的O(nlogn)
  排序
  树状数组
  heap
  Dijkstra
  SPFA

• n ≤ 10^7，O(n)
  双指针扫描
  KMP
  AC自动机
  线性筛素数

• n ≤ 10^9，O(√n)
  判断质数

• n ≤ 10^18，O(log⁡n)
  最大公约数
  快速幂

• n ≤ 10^1000，O((logn)^2)
  高精度加减乘除

• n ≤ 10^100000，O(logn × loglogn)
  高精度加减
  FFT/NTT

计算代码的时间复杂度

• 看循环，几层循环就是 n 的几次方
• 递归：主定理
  logn 层，每层 O(n)
• spfa、匈牙利算法、最大流算法理论时间复杂度特别高，实际运行效率非常快
• log(10^x) 稍大于 3x，可以估算

空间复杂度

单位

可以直接敲代码计算程序占据空间多少MB

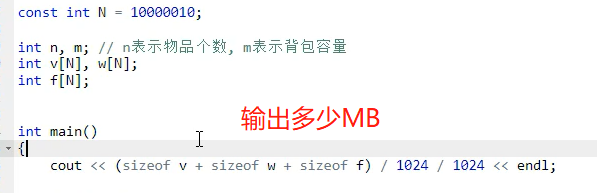
64 MB = 2^6 * 2^20 Byte = 2^26 Byte
2^26 / 2^2 = 2^24 （个）
64MB 至多开 1600 万个 int

递归会占据栈的空间