类型一:事先把C数组预处理出来(递推)
题目背景

思路
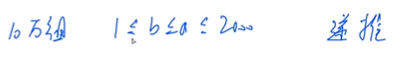


根据组合数递推公式,先把要用到范围内的组合数事先预处理打表出来
$C_{a}^{b}=C_{a-1}^{b}+C_{a-1}^{b-1}$
证明:
在a个球中取b个球,有多少种取法?
有$C_{a}^{b}$种
可以认为有一个球c十分特别,那取b个球就有两种取法:取到c还是不取到c
取到c: $C_{a-1}^{b-1}$(在另外a-1个球中取b-1个)
取不到c: $C_{a-1}^{b}$(在a-1个球里取b个)
//题目背景:AcWing 885
#include<iostream>
using namespace std;
const int N=2010,mod=1e9+7;
int c[N][N];
void init()
{
for(int i=0;i<N;i++) //N是组合数下标的上限
for(int j=0;j<=i;j++)
if(!j) c[i][j]=1; //如果上标为0,那表示一个也不取,只有一种情况,注意这里不是0,而是1
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; //计算的时候要取模
}
模板代码
//题目背景:AcWing 885
#include<iostream>
using namespace std;
const int N=2010,mod=1e9+7;
int c[N][N];
void init()
{
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++)
if(!j) c[i][j]=1;
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
int main()
{
init();
int n,a,b;
scanf("%d",&n);
while(n--)
{
scanf("%d%d",&a,&b);
printf("%d\n",c[a][b]);
}
return 0;
}
类型二:预处理出阶乘
题目背景

思路


+ 这个题为什么要求出逆元呢,直接除以相应的阶乘不行吗?


模板代码
//题目背景 AcWing 886
#include<iostream>
using namespace std;
const int N=100010,mod=1e9+7;
typedef long long LL;
int fact[N],infact[N];
int n,a,b;
int qmi(int a,int b,int p) //快速幂算法
{
int res=1;
while(b)
{
if(b&1) res=(LL)res*a%p;
a=(LL)a*a%p;
b=b>>1;
}
return res;
}
int main()
{
fact[0]=1,infact[0]=1;
for(int i=1;i<N;i++) //预处理出阶乘和阶乘的逆元
{
fact[i]=(LL)fact[i-1]*i%mod;
infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;
}
scanf("%d",&n);
while(n--)
{
scanf("%d%d",&a,&b);
printf("%d\n",(LL)fact[a]*infact[b]%mod*infact[a-b]%mod);
}
return 0;
}
(LL)左边都是int值,说明确定最终结果是一个int范围内的值,因为最终都模上mod了嘛!但是在具体的计算过程中先相乘的话可能会爆int,如果用int存的话可能导致数据错误,所以这里(LL)的作用应该是将数据暂时在LL的范围内计算,以保证正确性,最终再得到一个int的结果。
类型三:利用卢卡斯定理递归缩小范围
题目背景

组合数上下限范围都特别大
思路
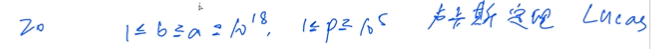
利用lucas定理进行化简计算
lucas定理内容:
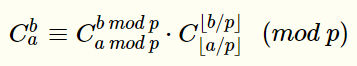
利用卢卡斯定理不断向下递归,把a、b缩小成比p小的数,再直接计算阶乘。
时间复杂度:
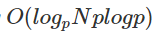
模板代码
//题目背景:AcWing 887
#include<iostream>
using namespace std;
typedef long long LL;
int n,p;
LL a,b;
int qmi(int a,int b,int p) //快速幂算法
{
int res=1;
while(b)
{
if(b&1) res=(LL)res*a%p;
a=(LL)a*a%p;
b=b>>1;
}
return res;
}
int C(int a,int b,int p) //直接计算组合数
{
if(b>a) return 0;
int res=1;
for(int i=1,j=a;i<=b;i++,j--)
{
res=(LL)res*j%p;
res=(LL)res*qmi(i,p-2,p)%p;
}
return res;
}
int lucas(LL a,LL b,int p) //卢卡斯定理
{
if(a<p&&b<p) return C(a,b,p);
else return (LL)C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main()
{
scanf("%d",&n);
while(n--)
{
scanf("%lld%lld%d",&a,&b,&p);
printf("%d\n",lucas(a,b,p));
}
return 0;
}
类型四:把数精确的算出来,不再取模(高精度乘法)
题目背景

思路
先分解质因数,再利用高精度乘法把这个组合数算出来。
具体步骤:
+ 1.把$1-a$之间的所有素数筛出来 (线性筛法)
void get_primes(int n)
{
for(int i=2;i<=n;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]*i<=n;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)break;//==0每次漏
}
}
}
- 计算出$C_{a}^{b}$中$1-a$之间的所有素数各含有多少个
原理:

int get(int n,int p)
{
int res =0;
while(n)
{
res+=n/p;
n/=p;
}
return res;
}
//主函数内
for(int i=0;i<cnt;i++)
{
int p = primes[i];
sum[i] = get(a,p)-get(a-b,p)-get(b,p);
}
- 用高精度乘把所有质因子乘上
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
//主函数内
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
for (int j = 0; j < sum[i]; j ++ )//primes[i]的次数
res = mul(res, primes[i]);
- 输出答案
for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
模板代码
#include<iostream>
#include<vector>
using namespace std;
int a,b;
const int N=5010;
int primes[N],cnt,sum[N];
bool st[N];
void get_primes(int n) //线性筛法
{
for(int i=2;i<=n;i++)
{
if(!st[i]) primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0) break;
}
}
}
int get(int n,int p) //计算该素数出现的次数
{
int res=0;
while(n)
{
res+=n/p;
n/=p;
}
return res;
}
vector<int> mul(vector<int> a,int b) //高精度乘法
{ //这里b一定不会为0
vector<int> c;
int t=0;
for(int i=0;i<a.size()||t;i++)
{
if(i<a.size()) t+=a[i]*b;
c.push_back(t%10);
t/=10;
}
return c;
}
int main()
{
scanf("%d%d",&a,&b);
get_primes(a); //筛素数
for(int i=0;i<cnt;i++) //计算素数出现的次数
{
int p=primes[i];
sum[i]=get(a,p)-get(b,p)-get(a-b,p);
}
vector<int> res;
res.push_back(1); //赋初值为1
//分解质因数,得到了质因数,也得到了每个质因数的次数,这时候就反复的把它们乘起来,利用高精度乘法来算
for(int i=0;i<cnt;i++)
for(int j=0;j<sum[i];j++)
res=mul(res,primes[i]);
for(int i=res.size()-1;i>=0;i--) printf("%d",res[i]);
return 0;
}

