第三讲 数学与简单DP

$$ \color{red}{总结：复习了一下DP还有DFS，了解了大致的做题方法} $$

几个常见的模型：

• 路线问题
• 背包问题（组合模型）
• 最长上升子序列}

AcWing 1205. 买不到的数目
AcWing 1211. 蚂蚁感冒
AcWing 1216. 饮料换购
AcWing 2. 01背包问题
AcWing 1015. 摘花生
AcWing 895. 最长上升子序列
AcWing 1212. 地宫取宝
AcWing 1214. 波动数列

1.买不到的数目

考察数学推导，可以认为是个结论

//买不到的数目
//数学推公式
#include<bits/stdc++.h>

using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    cout << (n - 1) * (m - 1) - 1 << endl;
    return 0;
}

暴力DFS搜索

//买不到的数目
//数学推公式
#include<bits/stdc++.h>

//实在太巧妙了
bool dfs(int m, int p, int q)
{
    if(m == 0) return true;

    if(m >= p && dfs(m - p, p, q)) return true;
    if(m >= q && dfs(m - q, p, q)) return true;

    return false;
}

int main()
{
    int p, q;
    cin >> p >> q;
    int res;
    //从1尝试到1000，寻找第一个不能被表示的数字
    for(int i = 1; i <= 1000; i++)
    {
        if(!dfs(i, p, q)) res = i;
    }
    cout << res << endl;

    return 0;
}

2.蚂蚁感冒

这道题目其实类似个脑筋急转弯，一旦考虑到蚂蚁碰面掉头返回等价于穿过，问题就变得相对简单。然后，依次分情况考虑所有的情况就行了。

//蚂蚁感冒
#include<bits/stdc++.h>

using namespace std;

const int N = 110;

int n;
int x[N];

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> x[i];

    int lr = 0, rl = 0;
    for(int i = 2; i <= n; i++)
    {
        if(abs(x[i]) < abs(x[1]) && x[i] > 0) lr++;
        if(abs(x[i]) > abs(x[1]) && x[i] < 0) rl++;
    }

    int res = 1;
    if(x[1] > 0)
    {
        res += rl;
        if(rl > 0) res += lr;
    }
    else
    {
        res += lr;
        if(lr > 0) res += rl;
    }
    cout << res << endl;

    return 0;
}

3.饮料换购

这道是个水题，直接模拟即可

//饮料换购
//模拟即可
#include<bits/stdc++.h>

using namespace std;

int main()
{
    int n;
    cin >> n;

    int res = n;
    res += n / 3;
    n = n / 3 + n % 3;//n表示瓶盖数量
    while(n >= 3)
    {
        res += n / 3;//换购
        n = n % 3 + n / 3;//总共的瓶盖
    }
    cout << res << endl;

    return 0;
}

4.01背包问题

01背包问题是十分经典的动态规划问题（组合模型），下面给出三种做法

• 常规动态规划（空间复杂度 $\color{red}{O(N^2)}$ ）
• 滚动数组优化版（空间复杂度 $\color{red}{O(N)}$ ）
• 记忆化搜索（不需要考虑计算的顺序）

常规动态规划

//01背包问题
//常规动态规划
#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m;
int w[N], v[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) 
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    }

    cout << f[n][m] << endl;

    return 0;
}

滚动数组优化版

//01背包问题
//滚动数组优化版
#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m;
int w[N], v[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
    {
        for(int j = m; j >= v[i]; j--)
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

记忆化搜索

//01背包问题
//记忆化搜索
#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int dp(int i, int j)
{
    int &u = f[i][j];
    if(u != -1) return u;

    u = dp(i - 1, j);
    if(j >= v[i]) u = max(u, dp(i - 1, j - v[i]) + w[i]);
    return u;
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    //初始化
    memset(f, -1, sizeof f);
    for(int i = 0; i <= n; i++) f[i][0] = 0;
    for(int i = 0; i <= m; i++) f[0][i] = 0;

    cout << dp(n, m) << endl;

    return 0;
}

5.摘花生

这个是路线类型的经典题目

//摘花生
#include<bits/stdc++.h>

using namespace std;

const int N = 110;

int n, m;
int g[N][N], f[N][N];

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        memset(f, 0, sizeof f);
        cin >> n >> m;
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                cin >> g[i][j];
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + g[i][j];
            }
        }
        cout << f[n][m] << endl;
    }
    return 0;
}

6.最长上升子序列

//最长上升子序列
#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n;
int a[N];
int f[N];//一维,f[i]代表以a[i]结尾的长度
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];

    for(int i = 1; i <= n; i++)
    {
        f[i] = 1;//没有前一个
        for(int j = 1; j < i; j++)
        {
            if(a[j] < a[i])
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
    }

    int res = 0;
    for(int i = 1; i <= n; i++)
    {
        res = max(res, f[i]);
    }

    cout << res << endl;

    return 0;
}

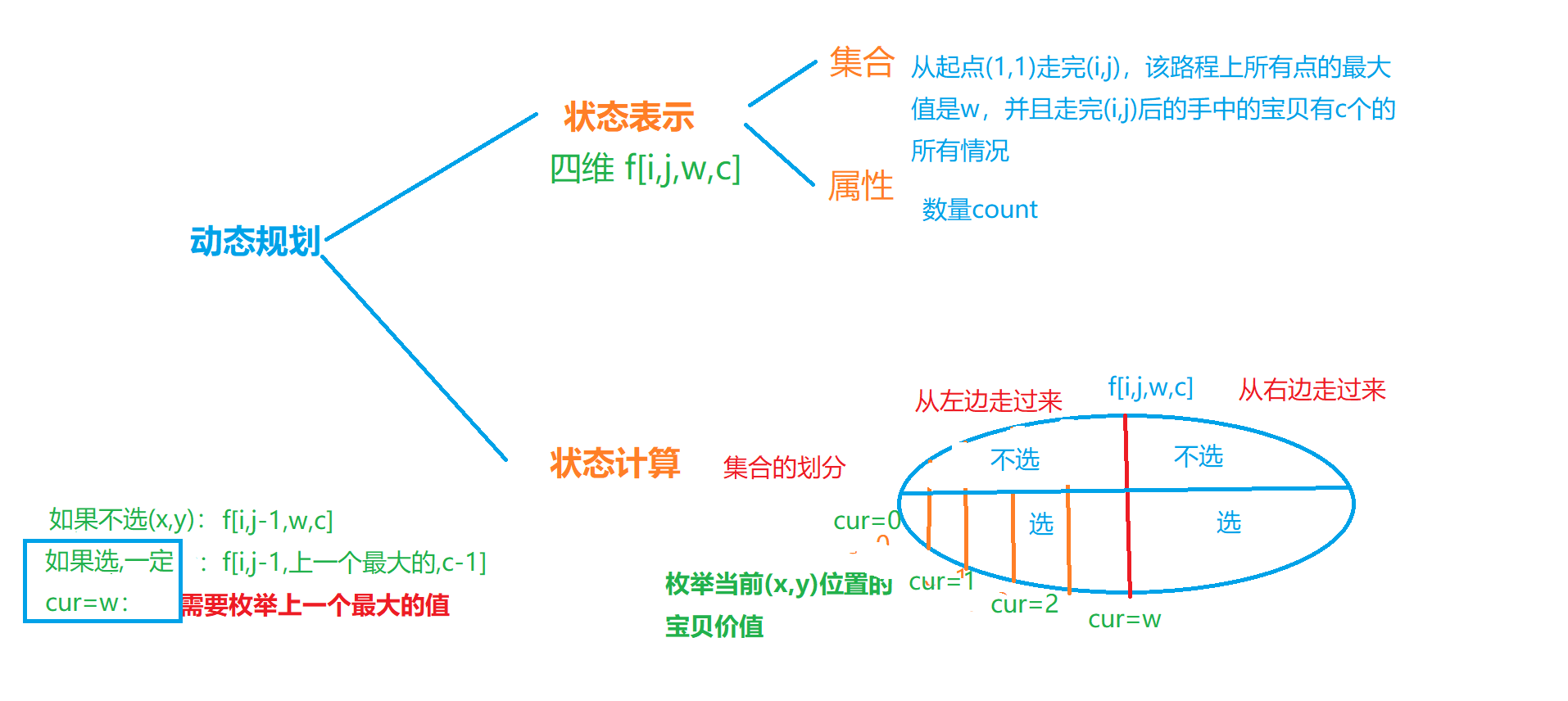
7.地宫取宝

这道题目维数比较多，还是很困难的，（不过可以写暴力DFS，虽然过不了）

正宗DP

ps：《关于我数组开的小了一位调了一个小时BUG的事情》

//地宫取宝
//正宗DP
#include<bits/stdc++.h>

using namespace std;

const int N = 55, P = 1000000007;

int n, m, k;
int g[N][N];
//第一维和第二维代表坐标，第三维代表走完(x,y)路程中最大的价值
//第四维代表当前走完(x,y)获取的宝贝数量
int f[N][N][14][15];

int main()
{
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> g[i][j];
            g[i][j]++;
        }
    }

    f[1][1][g[1][1]][1] = 1;
    f[1][1][0][0] = 1;//注意第三维的价值全部加了1

    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            if(i == 1 && j == 1) continue;
            for(int w = 0; w <= 13; w++)
            {
                for(int c = 0; c <= 13; c++)
                {
                    int &u = f[i][j][w][c];
                    //不选当前(x,y)的情况
                    u = (u + f[i][j-1][w][c]) % P;
                    u = (u + f[i-1][j][w][c]) % P;
                    //只有满足下面条件才能选当前
                    if(w > 0 && g[i][j] == w)
                    {
                        for(int t = 0; t < w; t++)
                        {
                            u = (u + f[i][j-1][t][c-1]) % P;
                            u = (u + f[i-1][j][t][c-1]) % P;
                        }
                    }
                }
            }
        }
    }

    int res = 0;
    for(int i = 1; i <= 13; i++)
    {
        res = (res + f[n][m][i][k]) % P;
    }
    cout << res << endl;

    return 0;
}

暴力DFS

//地宫取宝
//暴力DFS超时版
#include<bits/stdc++.h>

using namespace std;

const int N = 55, P = 1000000007;

int n, m, k;
int g[N][N];

int res;

//(x,y)是将要考虑的坐标,w是之前的最大值，c是之前的数量
void dfs(int x, int y, int w, int c)
{
    if(x > n || y > m) return;
    if(x == n && y == m)
    {
        if(c == k || c == k - 1 && g[x][y] > w)
            res = (res + 1) % P;
        return;
    }

    //不选(x,y)
    dfs(x + 1, y, w, c);
    dfs(x, y + 1, w, c);
    //选(x,y)
    if(g[x][y] > w)
    {
        dfs(x + 1, y, g[x][y], c + 1);
        dfs(x, y + 1, g[x][y], c + 1);
    }
}

int main()
{
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> g[i][j];
        }
    }

    dfs(1, 1, -1, 0);

    cout << res << endl;

    return 0;
}

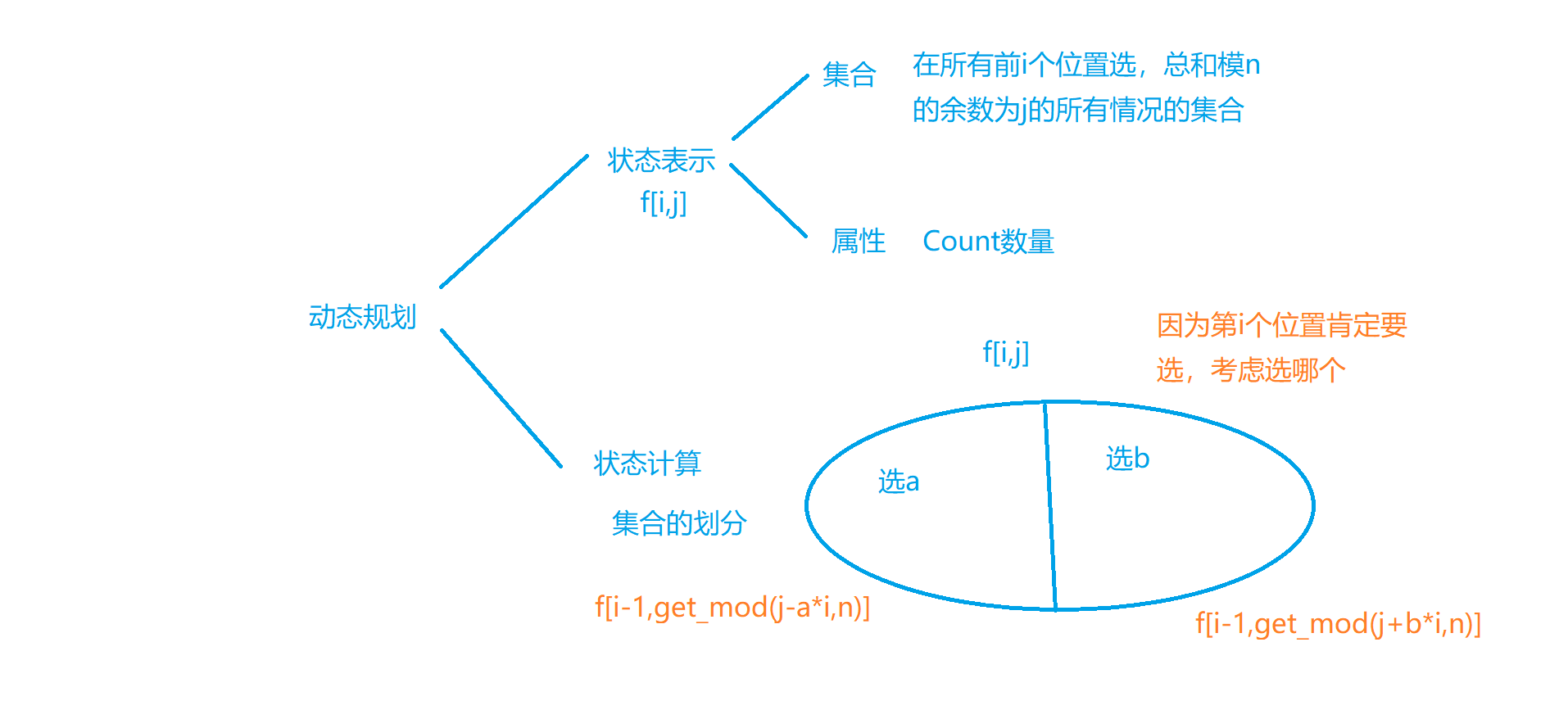
8.波动数列

这道题目的转化实在是太巧妙了，不容易找到问题的模型

//波动数列
//DFS过不了
#include<bits/stdc++.h>

using namespace std;

const int MOD = 100000007;

int n, s, a, b;

int res;

int get_mod(int x, int y)
{
    return (x % y + y) % y;
}

void dfs(int u, int sum)
{
    if(u == n)
    {
        if(get_mod(sum, n) == get_mod(s, n)) res++;
        return;
    }
    dfs(u + 1, sum + a * u);
    dfs(u + 1, sum - b * u);
}

int main()
{
    cin >> n >> s >> a >> b;

    dfs(1, 0);

    cout << res << endl;

    return 0;
}

//波动数列
//DP
#include<bits/stdc++.h>

using namespace std;

const int N = 1010, MOD = 100000007;

int n, s, a, b;
int f[N][N];

int get_mod(int x, int y)
{
    return (x % y + y) % y;
}

int main()
{
    cin >> n >> s >> a >> b;

    f[0][0] = 1;//边界条件，第0个位置只能凑出0，不能凑出其他所有数字

    for(int i = 1; i <= n - 1; i++)
    {
        for(int j = 0; j < n; j++)
        {
            f[i][j] = (f[i-1][get_mod(j-a*i,n)] + f[i-1][get_mod(j+b*i,n)]) % MOD;
        }
    }

    cout << f[n-1][get_mod(s, n)] << endl;

    return 0;
}