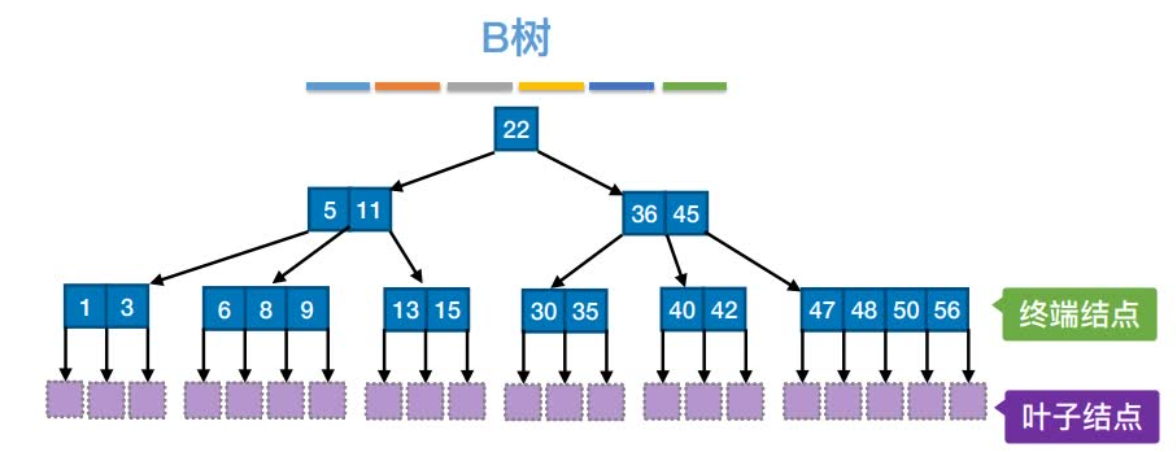
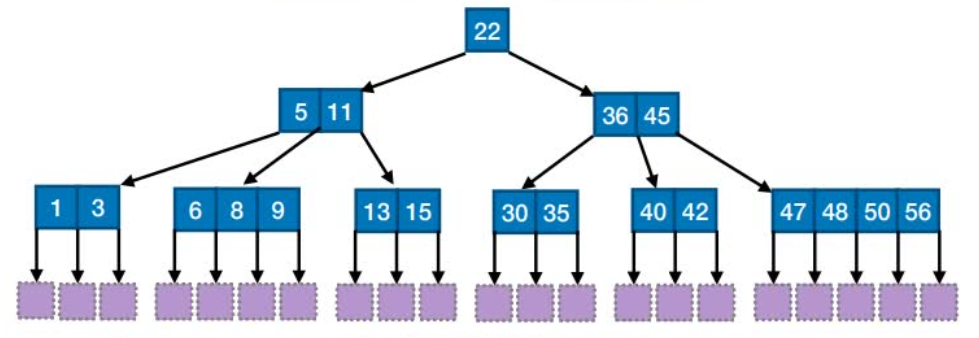
B树，⼜称多路平衡查找树，B树中所有结点的孩⼦个数的最⼤值称为B树的阶，通常⽤m表示。⼀棵m阶B树或为空树，或为满⾜如下特性的m叉树：
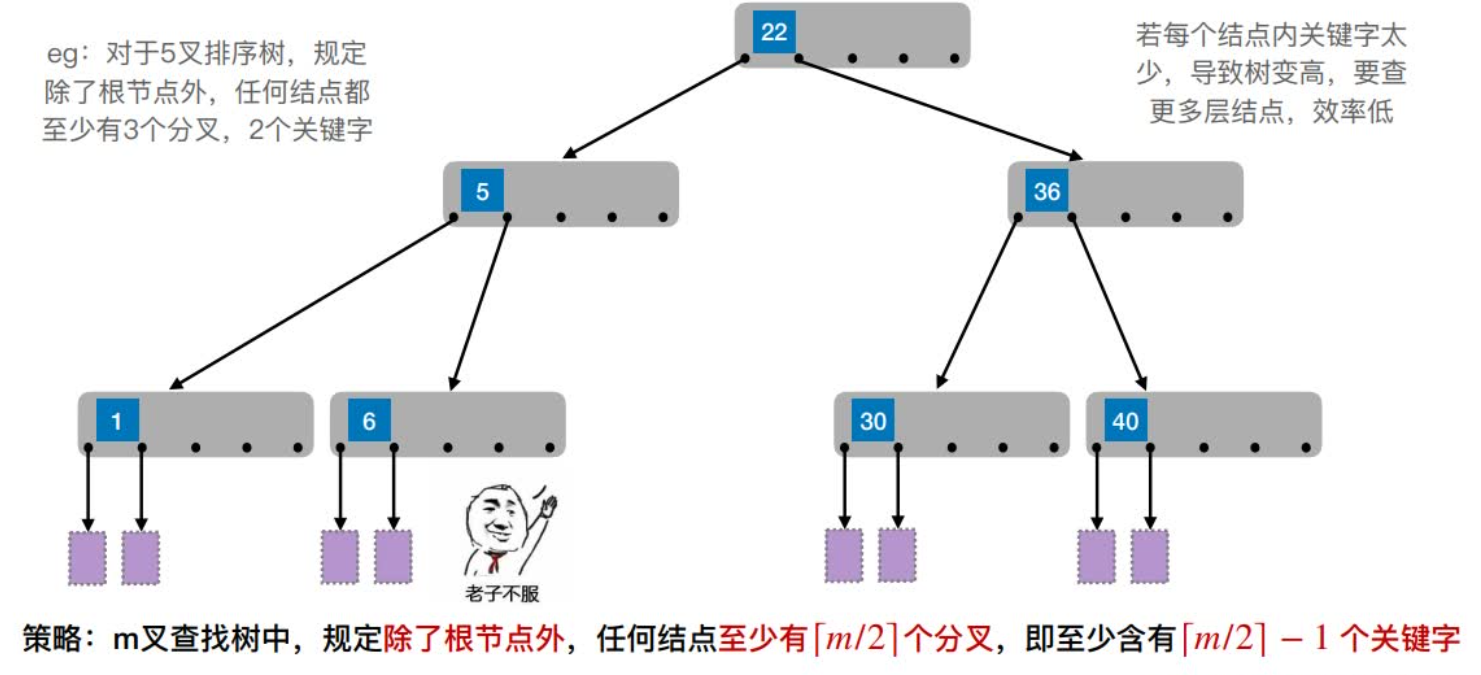
（1）树中每个结点⾄多有m棵⼦树，即⾄多含有m-1个关键字。
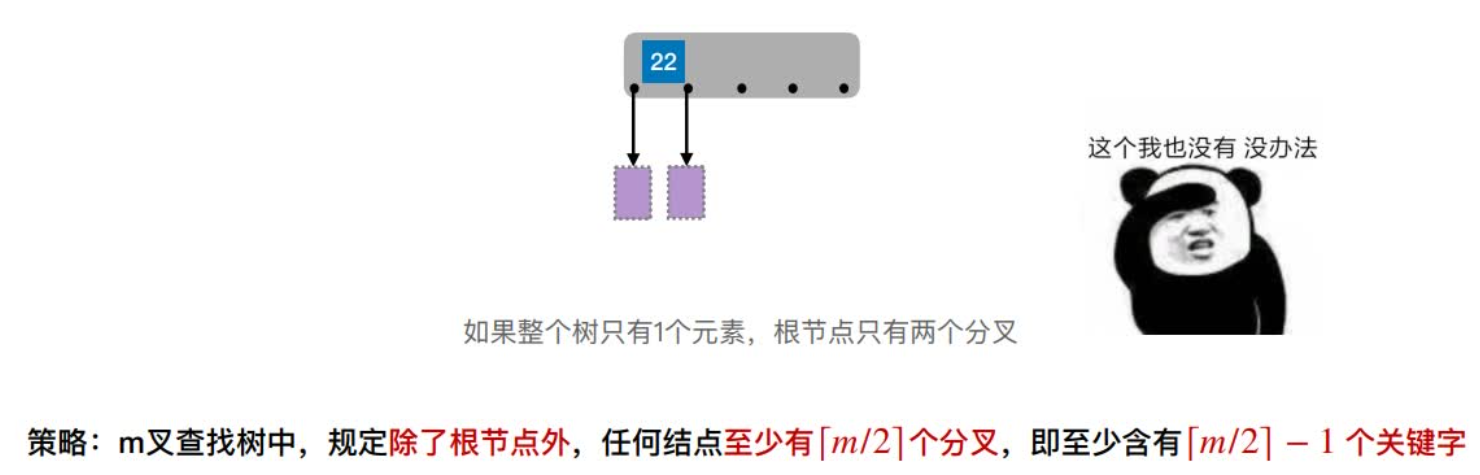
（2）若根结点不是终端结点，则⾄少有两棵⼦树。
（3）除根结点外的所有⾮叶结点⾄少有棵⼦树，即⾄少含有-1个关键字。
（4）所有⾮叶结点的结构如下：

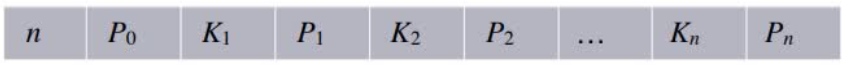
其中，Ki（i = 1, 2,…, n）为结点的关键字，且满⾜K1 < K2 <…< Kn；Pi（i= 0, 1,…, n）为指向⼦树根结点的指针，且指针Pi-1所指⼦树中所有结点的关键字均⼩于Ki，Pi所指⼦树中所有结点的关键字均⼤于Ki，n（⌈m/2⌉- 1≤n≤m - 1）为结点中关键字的个数。
（5）所有的叶结点都出现在同⼀层次上，并且不带信息（可以视为外部结点或类似于折半查找判定树的查找失败结点，实际上这些结点不存在，指向这些结点的指针为空）。
特性
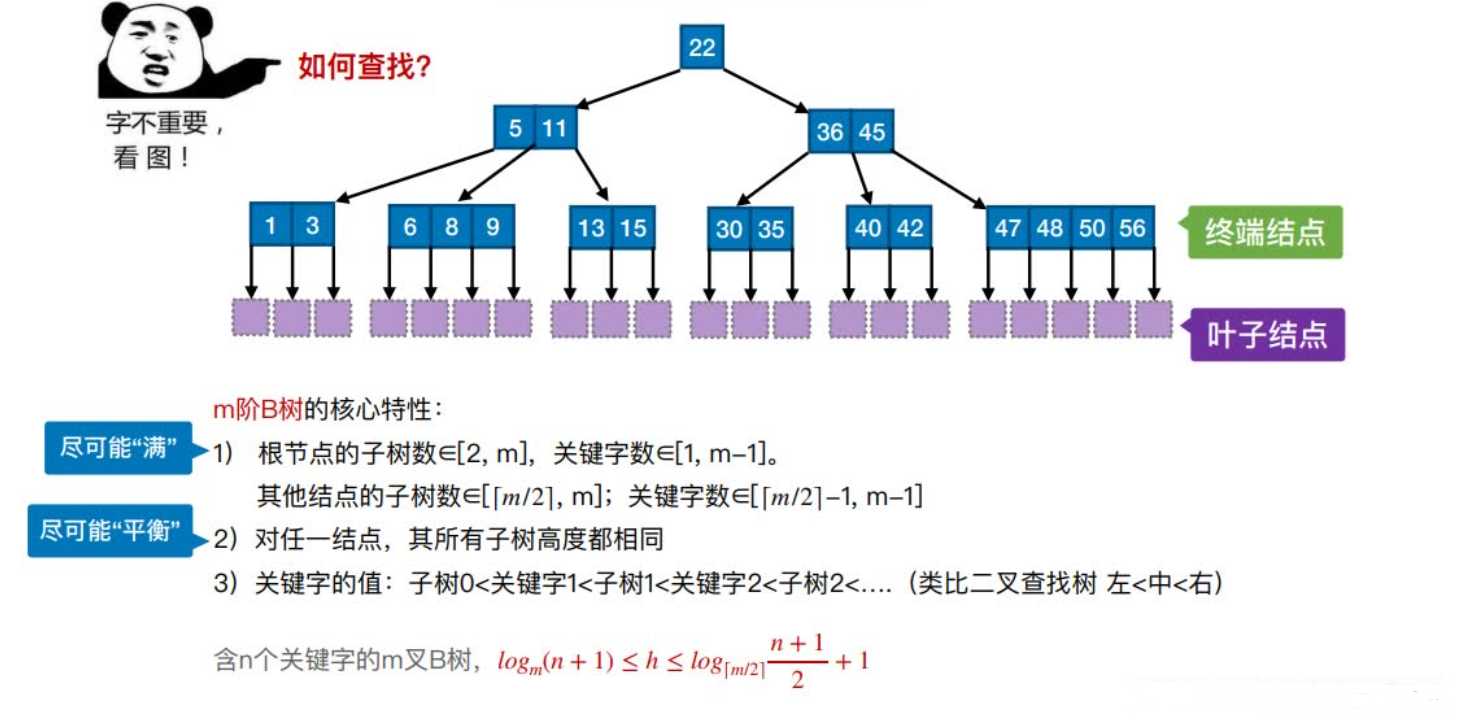
m阶B树的核⼼特性：

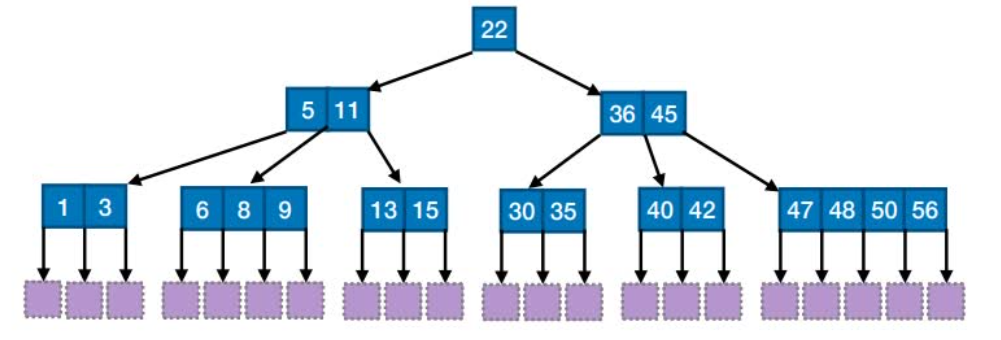
（1）根节点的⼦树数∈[2, m]，关键字数∈[1, m-1]。其他结点的⼦树数∈[⌈m/2⌉, m]；
关键字数∈[⌈m/2⌉-1, m-1]
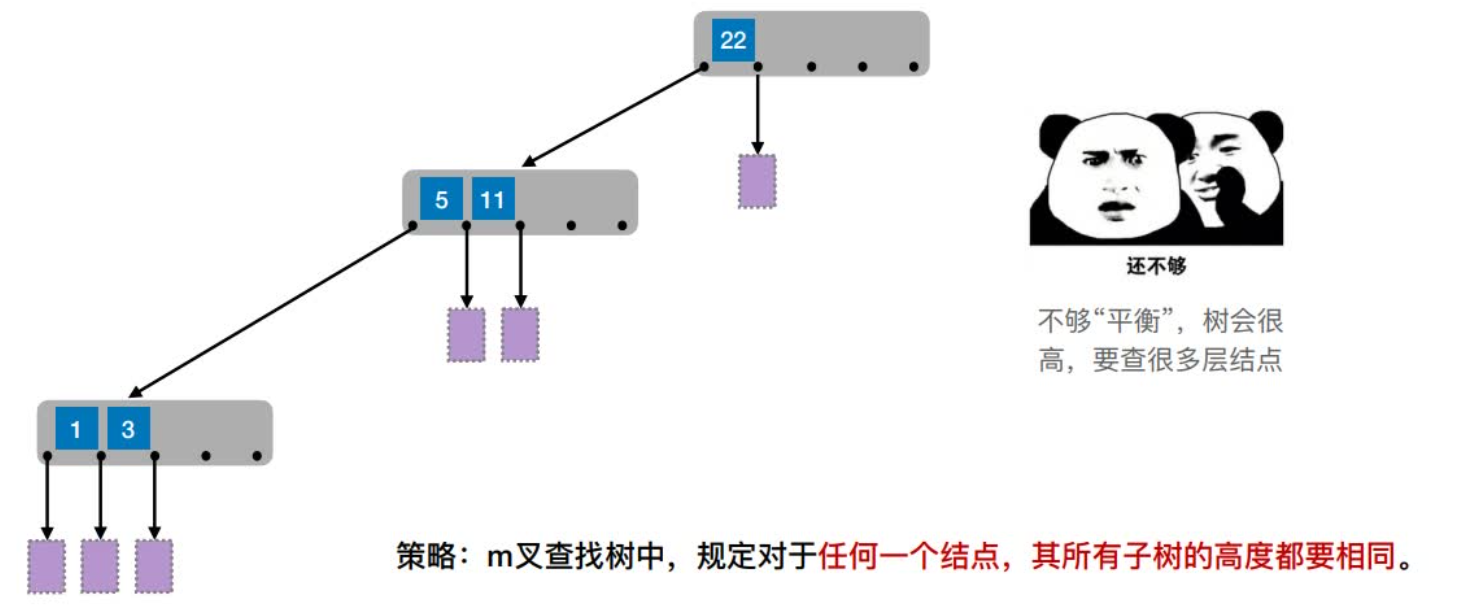
（2）对任⼀结点，其所有⼦树⾼度都相同
（3）关键字的值：⼦树0<关键字1<⼦树1<关键字2<⼦树2<…. (类⽐⼆叉查找树 左<中<右)
操作





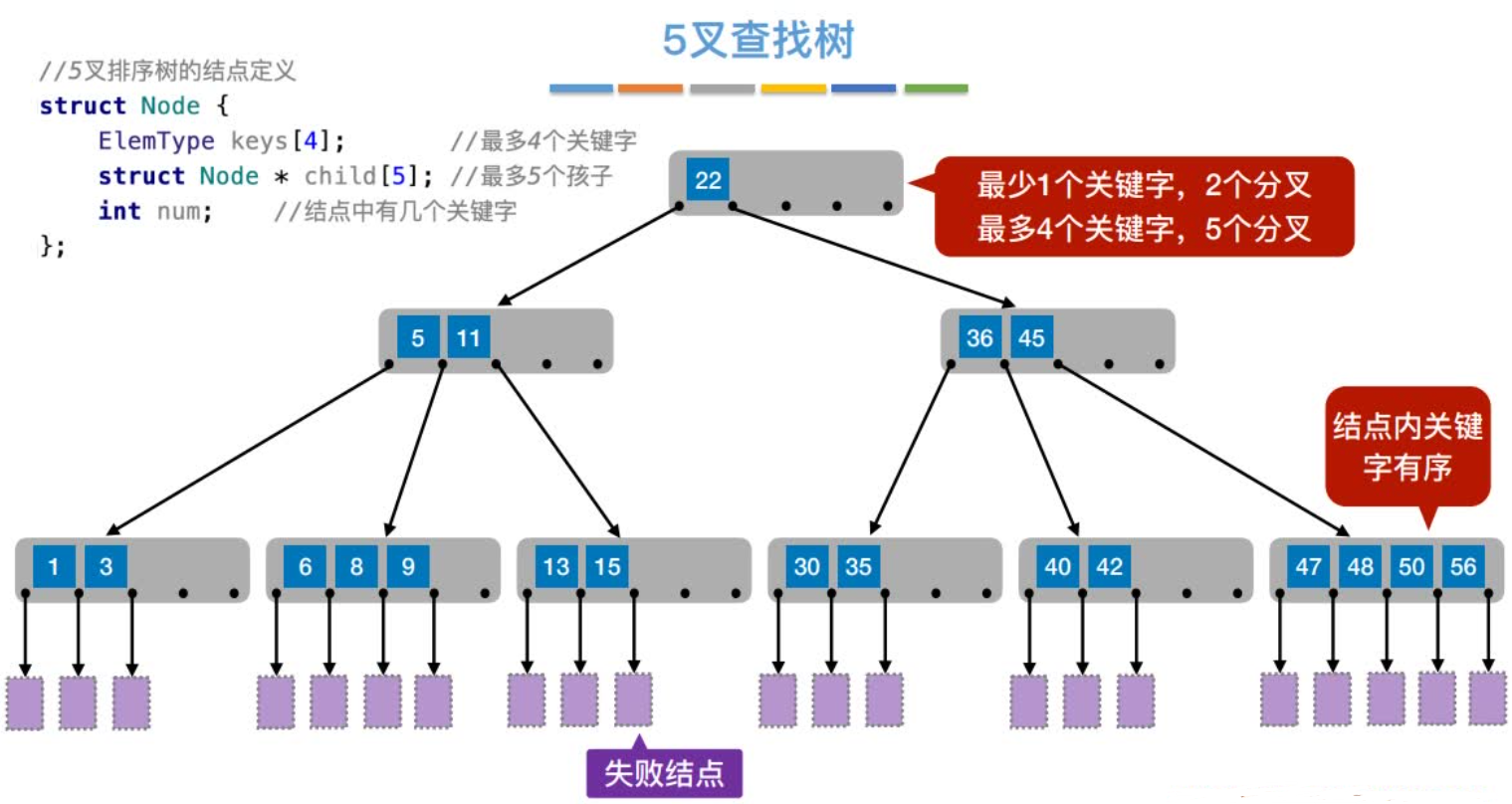
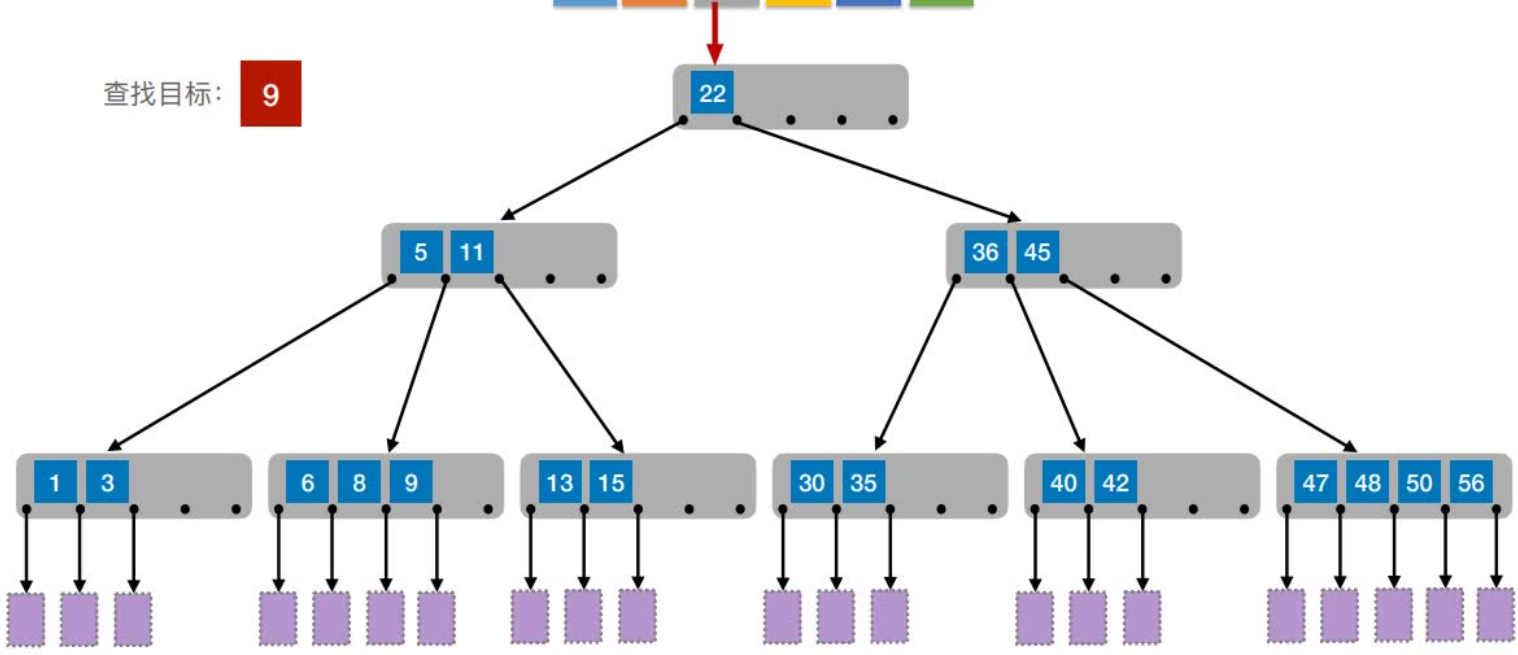
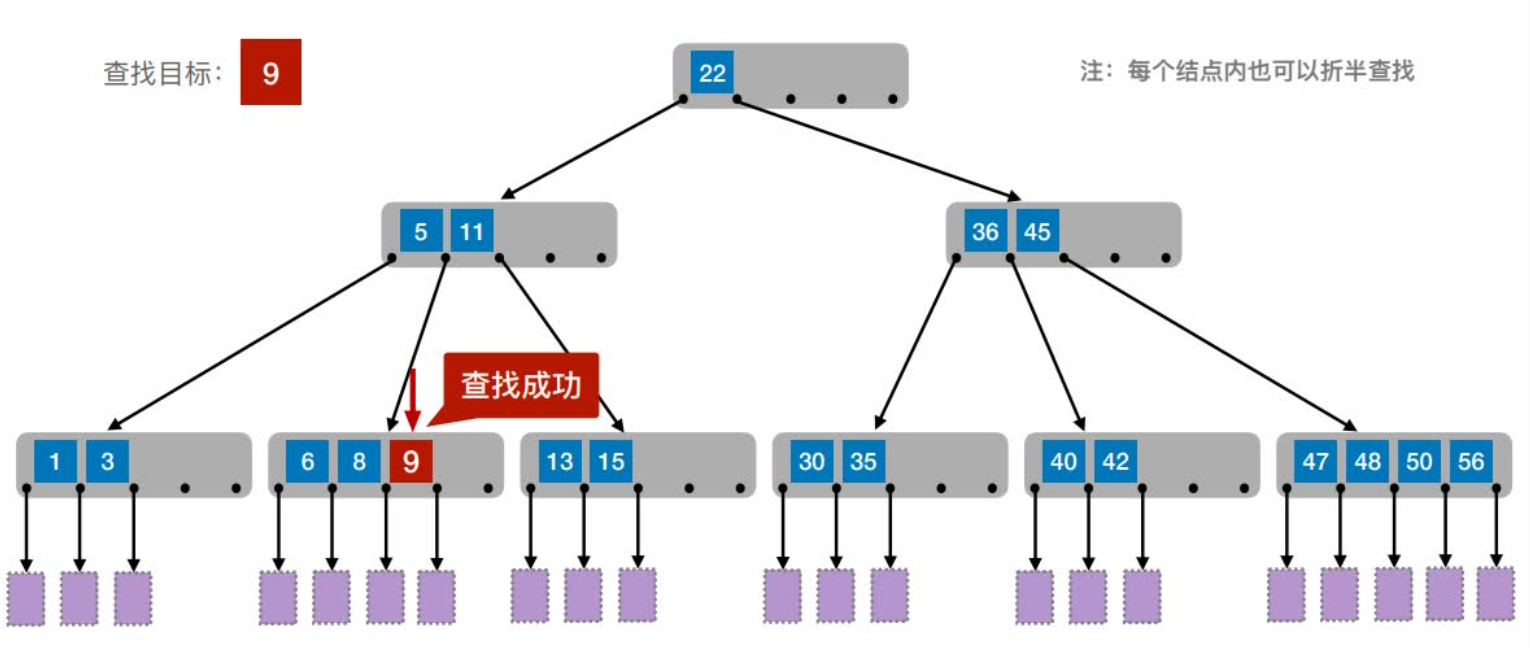
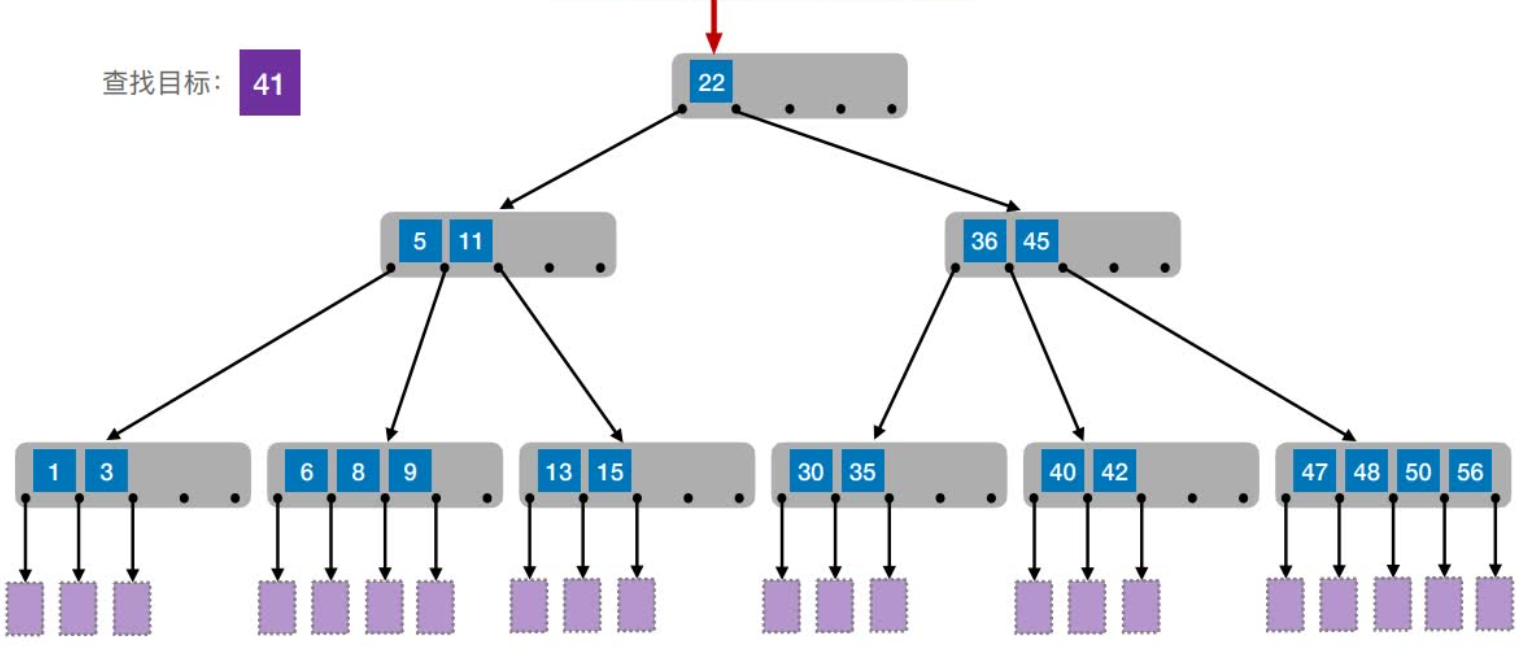
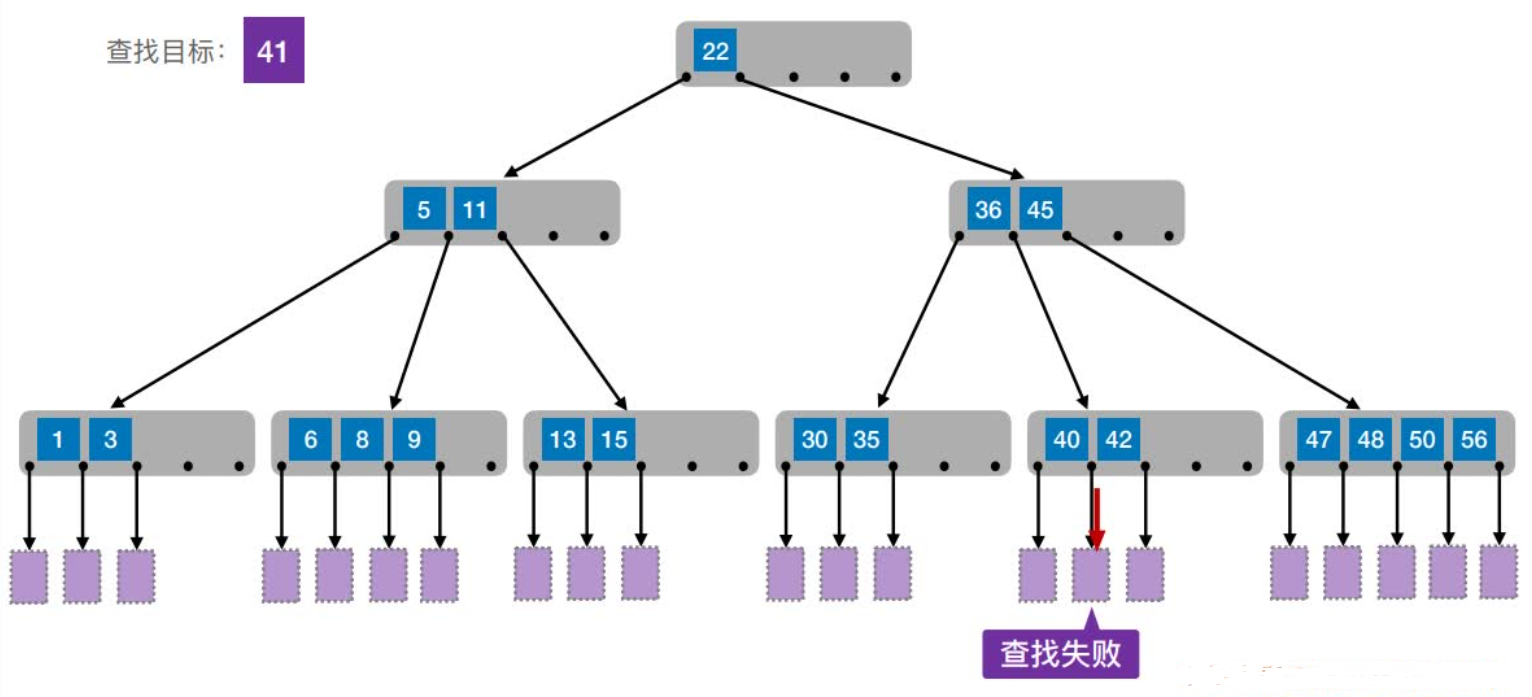
如何保证查找效率



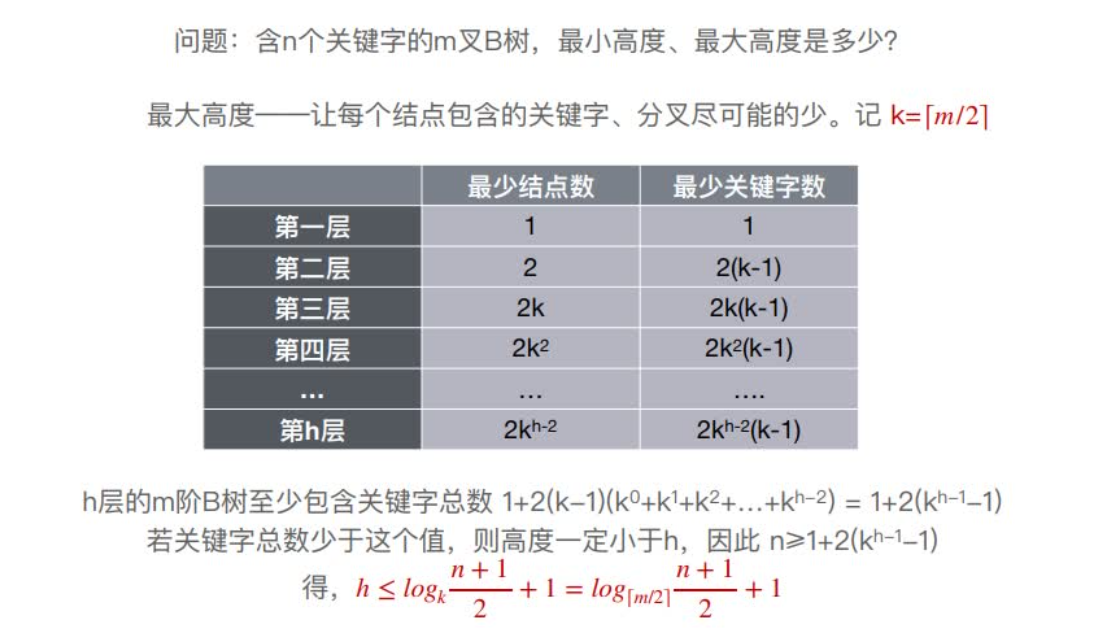
B树的⾼度

注：⼤部分学校算B树的⾼度不包括叶⼦结点（失败结点）




总结