原理

不看每项的系数，容斥原理公式的每一项合起来，其实是把所有情况都选择了一遍（只选一个，只选两个，只选三个，只选四个......），除了一个也不选的情况。然后每项的系数，随着选中数目的增加，在1和-1之间交替。

应用举例

题目背景

思路

这是一道典型的容斥原理应用题。



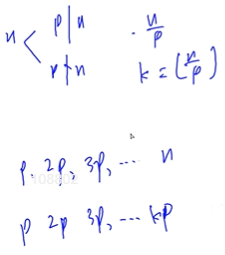
求1~n中有多少数是p的倍数，即n/p（下取整）
求1~n中有多少数既是p1的倍数，也是p2的倍数，即求1到n中有多少数是它们最小公倍数的倍数：n/（p1p2）（因为p1和p2是质数，没有公因子，所以它们的最小公倍数就是它们的乘积*）

m个数，对应了$2^{m}$种选法，但是这里不考虑一个都不选的，所以总共有$2^{m}-1$种选法。
可以用位运算的0，1来反映选不选的中的情况。
1~111…111（m个1）正好反映了$2^{m}-1$种选法。

模板代码

//题目背景：AcWing 890
#include<iostream>
using namespace std;
typedef long long LL;
const int N=20;
int n,m,p[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++) scanf("%d",&p[i]);  //读入质数
    int res=0;//存储总数
    for(int i=1;i<1<<m;i++)    //枚举1~2的m次方-1，每个数的m位二进制表示，表示了一种选择的情况
    {
        int t=1;  //选中的质数的乘积，即它们的最小公倍数
        int s=0;  //选中了几个数
        for(int j=0;j<m;j++)    //遍历当前遍历到的这个数的m位中的每一位
        {
            if(i>>j&1)  //如果当前位为1，证明选中了它
            {
                if((LL)t*p[j]>n)   //但是如果这个时候公倍数已经大于n了，说明1~n中不含有同时能整除这几个选中的质数的数
                {
                    t=-1;    //t=-1作为退出标记
                    break;    //退出内层循环
                }
                t=(LL)t*p[j];  //如果不是上述情况，就把选中的质数乘到t上去
                s++;           //选中数量++
            }
        }
        if(t==-1) continue;   //识别到退出标记，continue继续循环

        if(s&1) res+=n/t;   //如果当前这个数反映的选择情况是选择了奇数个，则作加法
        else res-=n/t;      //是偶数，作减法
    }
    printf("%d",res);
    return 0;
}