leetcode 329 https://leetcode.com/problems/longest-increasing-path-in-a-matrix/
直接暴力DFS会超时

暴力DFS
class Solution {
int res = 0;
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
int n;
int m;
int[][] matrix;
List[HTML_REMOVED] list;

public int longestIncreasingPath(int[][] _matrix) {
    matrix = _matrix;
    n = matrix.length;
    m = matrix[0].length;
    if(n == 1 && m == 1) return 1;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            dfs(i, j, 1);
        }
    }
    return res;
}

public void dfs(int x, int y, int ans){
    if(ans > res) res = ans;
    if(x < 0 || x >= n || y < 0 || y >= m) return;
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i];
        int ny = y + dy[i];
        if(nx >= 0 && nx < n && ny >= 0 && ny < m && matrix[nx][ny] > matrix[x][y] ){
            dfs(nx, ny, ans + 1);    
        }
    }
}

}

超时的原因是 重复计算了很多，比如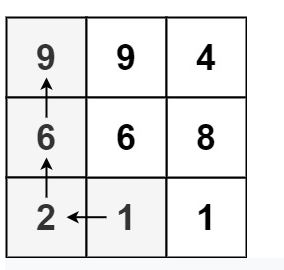
比如2 -> 6 -> 9 这条路径上已经判断了一次 6->9 的距离，下一次 起始点是6时候，又判断了一次 6 -> 9， 就进行了重复的判断。如果能够记录 6 -> 9 这条路径上6能到达的最大值，那么2 ->6->9的时候，2 ->6 直接纳6的值就做到了优化

DFS 加记忆化优化
class Solution {

int res = 0;
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
int n;
int m;
int[][] matrix;
int[][] cache;
List<int[]> list;

public int longestIncreasingPath(int[][] _matrix) {
    matrix = _matrix;
    n = matrix.length;
    m = matrix[0].length;
    cache = new int[n][m];

    for(int i = 0; i < n; i++) Arrays.fill(cache[i], -1);

    if(n == 1 && m == 1) return 1;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            int len = dfs(i, j);
            res = Math.max(res, len);
        }
    }
    return res;
}

public int dfs(int x, int y){  //x y这点能到达的最长距离
    if(cache[x][y] != -1) return cache[x][y];
    cache[x][y] = 1;
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i];
        int ny = y + dy[i];
        if(nx < 0 || nx >= n || ny < 0 || ny >= m || matrix[nx][ny] <= matrix[x][y]) continue;
        int len = 1 + dfs(nx, ny);
        cache[x][y] = Math.max(cache[x][y], len);
    }
    return cache[x][y];
}

}

暴力DFS是正着从1开始往下走，记忆化搜索和dfs加记忆化数组优化是反着推状态
递归思想的记忆化搜索
最后比较的时候，f[x][y] = Math.max(f[x][y], dfs(nx, ny));
例如 6 可以朝9， 朝6， 朝2走，可能第一次朝2走是一个值，朝6走发现比朝2走还大，所以要取到最大的f[x][y]
class Solution {

int[][] g;
int[][] f;
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
int n;
int m;

public int longestIncreasingPath(int[][] matrix) {
    g = matrix;
    n = matrix.length;
    m = matrix[0].length;
    f = new int[n][m];

    for(int i = 0; i < n; i++) Arrays.fill(f[i], -1);
    int res = 0;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            res = Math.max(res, dp(i, j));
        }
    }
    return res;
}

public int dp(int x, int y){
    if(f[x][y] != -1) return f[x][y];
    f[x][y] = 1;
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i];
        int ny = y + dy[i];
        if(nx >= 0 && nx < n && ny  >= 0 && ny < m && g[nx][ny] > g[x][y]){
            f[x][y] = Math.max(f[x][y], dp(nx, ny) + 1);  
        }
    }
    return f[x][y];
}

}