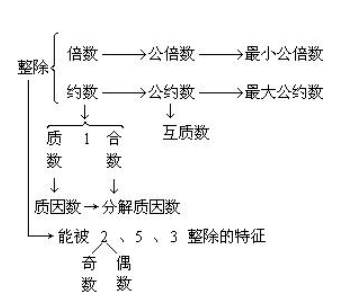
质数

只有1和自己两个约数

合数

合数指自然数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。在自然数中不是质数的就是合数，质数和合数是对立的，两者互为补集

约数

如果一个整数能被两个整数整除，那么这两个数就是这个数的约数。 约数是有限的，一般用最大约数。 直白地说:约数就是能将其整除的除数. 约数是可以整除这个数的数,一般都小于或等于它 (包括它自身).

公约数和最大公约数

公约数(也叫“公因数”)：如果一个整数同时是其它几个整数的约数，我们称这个整数为其它几个整数的“公约数”。公约数中最大的我们称之为这几个整数的最大公约数。

公倍数

指在两个或两个以上的自然数中，如果它们有相同的倍数，这些倍数就是它们的公倍数。公倍数中最小的，就称为这些整数的最小公倍数。

这两个定义并不难理解，举个简单的例子：比如对于正整数4和6，他们的公约数有1、2，其中2是最大公约数;公倍数有12 、24、……，其中最小公倍数是12。在这里由于最小公约数都是1，最大公倍数趋近于无穷大，因此公职类考试中只需要研 究最大公约数与最小公倍数。

互质整数和互质自然数

互质是公约数只有1的两个整数，叫做互质整数。公约数只有1的两个自然数，叫做互质自然数，后者是前者的特殊情形

互质,若N个整数的最大公因数是1，则称这N个整数互质。

例如8,10的最大公因数是2，不是1，因此不是整数互质。

7,11,13的最大公因数是1，因此这是整数互质。

5和5不互质，因为5和5的公因数有1、5。

1和任何数都成倍数关系，但和任何数都互质。因为1的因数只有1，而互质数的原则是：只要两数的公因数只有1时，就说两数是互质数。因为1只有一个因数所以1既不是质数（素数），也不是合数，无法再找到1和其他数的别的公因数了。1和-1与所有整数互素，而且它们是唯一与0互素的整数。

互质数的写法：如c与m互质，则写作（c,m）=1。

小学数学教材对互质数是这样定义的：“公约数只有1的两个数，叫做互质数。”

这里所说的“两个数”是指自然数。

“公约数只有 1”，不能误说成“没有公约数。”

这里有一个误区，认为0不与任何数互质。严格地按照互质的定义来看0与1，-1均互质，通过任意有理数的表示方式a/b（a,b互质且b为正整数），同样可以得出0与1，-1均必须互质，否则0不是有理数。