Dijkstra掌握朴素版本就可以
单源最短路:从一个点出发到各个点的最短路 O(n^2) (前提:边权非负数,如果负权可以用Bellman-Ford / SPFA)
如果你非要问我为啥不能求负权边,因为它的证明要保证每一条边是非负,具体证明考研不考,想学私信
朴素版本代码类似prim的朴素代码,原因是都需要维护集合和更新集合的过程也类似于扩展集合的过程,但是实则完全不同要区分好
注意:在选择填空中得出的每个点到源点的最短路径数值一定是严格递增的才是正确
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010, INF = 0x3f3f3f3f;
int n,m;
int g[N][N], dist[N];//稠密图一般使用邻接矩阵,记录每个节点距离起点的距离
bool st[N];//True表示已经确定最短路 属于s集合
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);//所有节点距离起点的距离初始化为无穷大
dist[1] = 0;//起点距离自己的距离为零
for (int i = 0; i < n; i ++ )//迭代n次,每次可以确定一个点到起点的最短路
{
int t = -1;//t的核心在于维护距离上一个最短路径最近的点
for (int j = 1; j <= n; j ++ )
//不在s集合,并且如果没有更新过,则进行更新, 或者发现更短的路径,则进行更新
if(!st[j] && (t == -1 || dist[j] < dist[t]))
t = j;
st[t] = true;//加入到s集合中
for (int j = 1;j <= n;j ++)//找到了距离最小的点t,并用最小的点t去更新其他的点到起点的距离
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
// 返回起点距离n号节点的最短距离
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m -- )
{
int a,b,c;
cin >> a >> b >> c;
g[a][b] = min(g[a][b],c);
}
int res = dijkstra();
if(res != INF) printf("%d\n",res);
else printf("-1\n");
return 0;
}
Floyd掌握整个实现的过程就好
策略:动态规划,三重寻欢推导图中两两点之间的最短距离,证明使DP方面的考研不考,代码能看懂过程能了解就行
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 210, INF = 0x3f3f3f3f;
int n,m,Q;
int d[N][N];
int main()
{
scanf("%d%d%d",&n,&m,&Q);
memset(d, 0x3f, sizeof d);
//初始化:每个点到自己的距离都是0
for(int i = 1;i <= n;i ++) d[i][i] = 0;
while (m --)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = min(d[a][b], c);
}
/*
三重for循环 DP策略 O(n^3)
思想:f(i,j,k)从i到j,中间经过所有点的编号是1~k的情况下的最短距离是多少
*/
for (int k = 1;k <= n;k ++)//
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);//更新 从i到k再到j 和 当前从i到j的距离
while (Q --)
{
int a, b;
scanf("%d%d", &a, &b);
int c = d[a][b];
if(c > INF / 2) //如果初始1->3和2->3是∞,而1->2是-2,则1->2->3就是∞-2,但实际1和3可能不连通则会造成比∞小一点
puts("impossible");
else
printf("%d\n", c);
}
return 0;
}
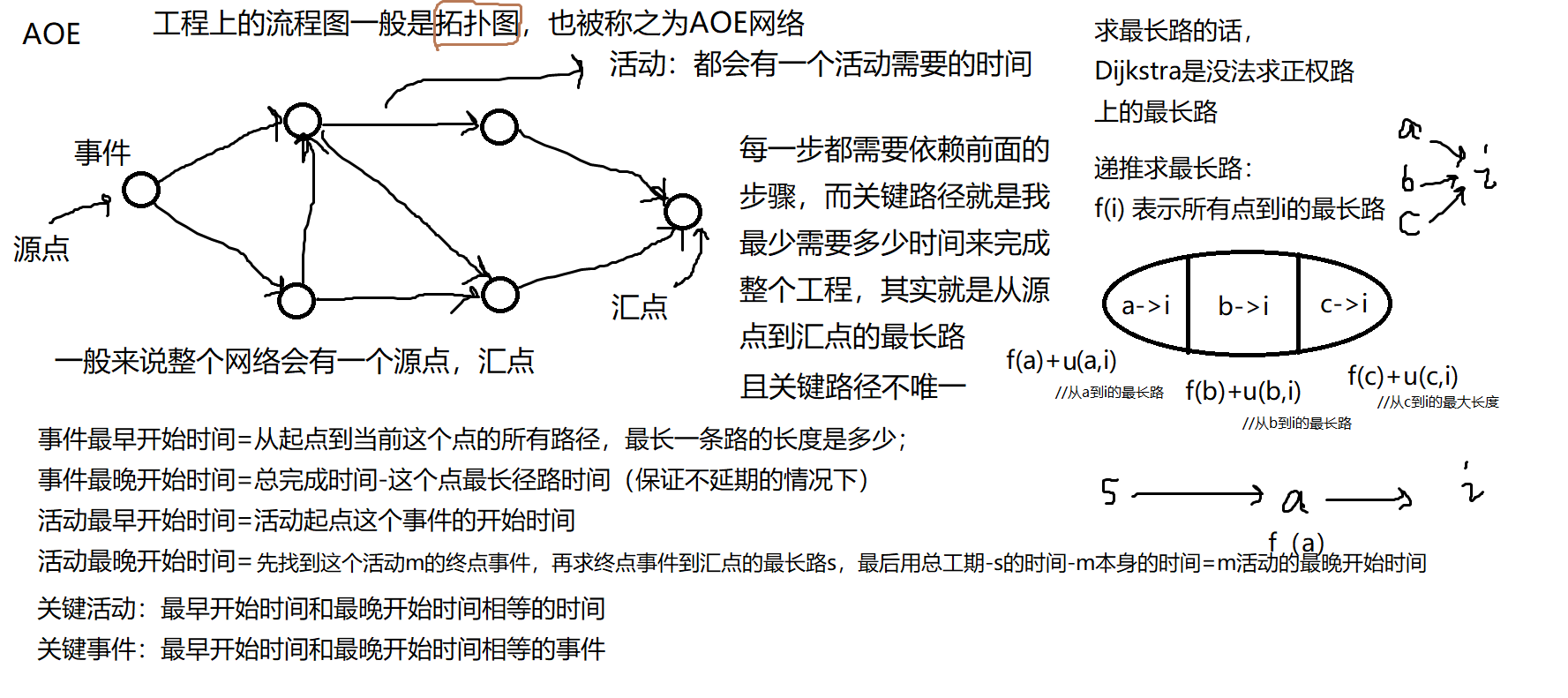
关键路径:就算是最短路的应用
AOE