问题： 给定汉诺塔的层数 $n$，目的是将 $a$ 柱上的 $n$ 个盘子全部移动至 $c$ 柱(且符合汉诺塔移动规则)，并依次输出盘子在 $a$ , $b$ , $c$ 三根柱子上的移动顺序.

一、递归实现

1. 当 $n$ 等于 $1$ 时，将 $a$ 柱上的盘子移动 $c$ 柱
2. 当 $n$ 大于 $1$ 时，先将 $a$ 柱上的 $n-1$ 个盘子移动到$b$柱,接着将 $a$ 柱上剩余的 $1$ 个盘子移动到 $c$ 柱,最后将 $b$ 柱上的 $n-1$ 个盘子移至 $c$ 柱.

递归版代码实现

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
/*递归版汉诺塔实现*/
void hanoi(int n, char A, char B, char C) //将A柱上的n个盘子借助B柱移动至C柱 
{
    if (n == 1) {
        printf("%c->%c\n", A, C);
        return;
    }
    hanoi(n - 1, A, C, B);
    printf("%c->%c\n", A, C);
    hanoi(n - 1, B, A, C);
}
int main() {
    int t; cin >> t;
    while (t--) {
        int n; cin >> n;
        hanoi(n, 'a', 'b', 'c');
    }
    return 0;
}

二、非递归实现（打表找规律）

在知乎上看到的一张图，根据这个图通过找规律实现非递归版的汉诺塔

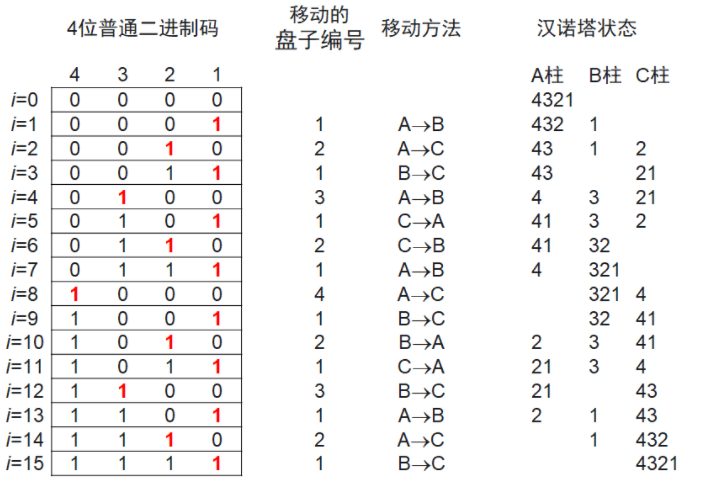
图片来源
1. 在这张图上我们可以看出每次移动的盘子编号就是左边二进制中最低位的1所在的位置
2. 只看某一个编号的话，我们会发现每次的移动操作是按照某个顺序循环出现的
3. 但是根据编号的奇偶，我们发现这个顺序是不一致的，当盘子编号是奇数时，移动顺序是$ABC$循环出现（$A$ -> $B$ ,$B$ -> $C$,$C$ -> $A$ …）;当盘子的编号是偶数时，移动顺序是 $ACB$循环出现
这是上图中找出的规律，此外，仅仅按这种规律实现出来，结果并不是最终的答案
在上面得出的规律的基础上，手动模拟出 $n$ 等于$3$ 时的情况，如下图所示：

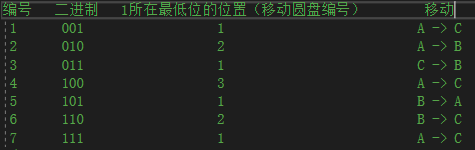
从此图中的规律基本上符合上述所得规律，唯一的不同点就是移动顺序稍有不同，当盘子编号为奇数时，移动顺序是$ACB$,当盘子编号是偶数时，移动顺序是$ABC$.
至此，所有的规律都找出来了，根据盘子总数n的奇偶和盘子编号的奇偶来判断移动顺序。

汉诺塔的非递归版实现（打表找规律）

#include <map>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<char, char> PCC;
/*汉诺塔的非递归找规律实现*/
char odd[3] = { 'a','b','c' };//奇数柱子顺序
char even[3] = { 'a','c','b' };//偶数柱子顺序
int lowbit(int x) {
    return x & -x;
}
int getpos(int x) {
    x = lowbit(x);
    int cnt = 0;
    while (x) {
        cnt++;
        x /= 2;
    }
    return cnt;
}
int num[10000010];
int main() {
    //freopen("test.txt", "w", stdout);
    int t; cin >> t;
    while (t--) {
        map<int, int> cnt;//记录某个圆盘被移动的次数
        map<int, PCC> res;
        int n; cin >> n;
        /*已知汉诺塔的移动次数是2^n-1次*/
        //生成移动盘子编号的序列
        for (int i = 1;i <= (1 << n) - 1;i++) {
            num[i] = getpos(i);
            cnt[num[i]]++;
            if (n % 2 == 0) {
                //n为偶数
                if (num[i] & 1) {
                    //移动的盘子编号为奇数
                    int k = cnt[num[i]];
                    res[i] = { odd[(k - 1) % 3],odd[k % 3] };
                }
                else {
                    //移动的盘子编号为偶数
                    int k = cnt[num[i]];
                    res[i] = { even[(k - 1) % 3],even[k % 3] };
                }
            }
            else {
                /*n为奇数*/
                if (num[i] % 2 == 0) {
                    //移动的盘子编号为偶数
                    int k = cnt[num[i]];
                    res[i] = { odd[(k - 1) % 3],odd[k % 3] };
                }
                else {
                    //移动的盘子编号为奇数
                    int k = cnt[num[i]];
                    res[i] = { even[(k - 1) % 3],even[k % 3] };
                }
            }
        }
        for (int i = 1;i <= (1 << n) - 1;i++) {
            cout << res[i].first << "->" << res[i].second << endl;
        }
    }
    return 0;
} 
/*
编号   二进制   1所在最低位的位置（移动圆盘编号）        移动
 1      001                  1                          A -> C
 2      010                  2                          A -> B
 3      011                  1                          C -> B
 4      100                  3                          A -> C
 5      101                  1                          B -> A
 6      110                  2                          B -> C
 7      111                  1                          A -> C
*/