A. Hard Way

简单计算几何

思路：观察样例下面的小字,把题目读懂.就相当于找这样的点集：

• 在三角形的边上存在某点能从$y=0$连接到该点,且不会穿过三角形内部.

观察样例很明显这样的点其实一定会构成一条边满足这样的条件:
$y_1 > y_2 , y_3 > y_2.且y_1=y_3 $.类似这样的式子.构成的边类似下图：

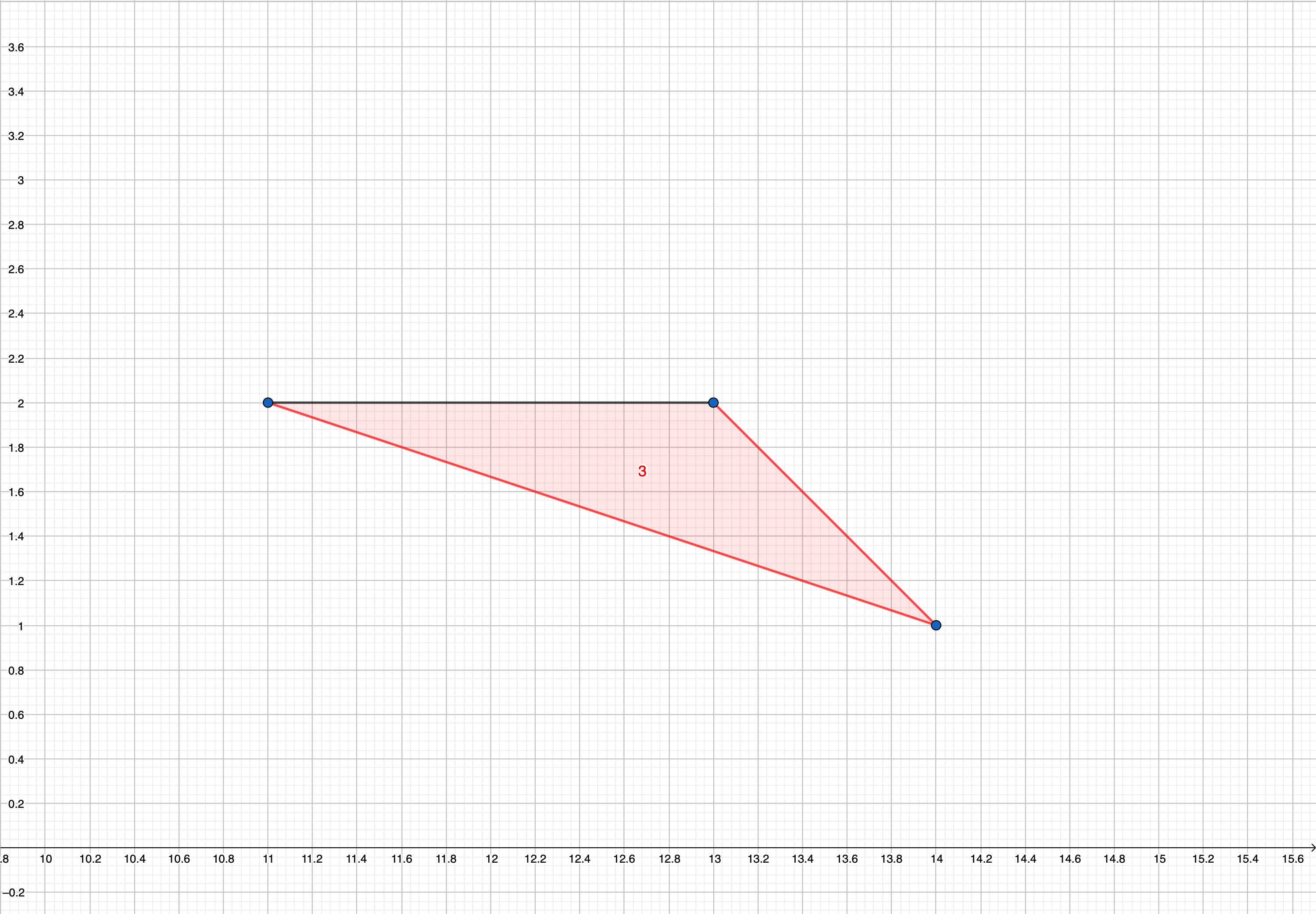
即一条横边平行x轴,且严格高于其他边.

AC Code:

#include<bits/stdc++.h>
#pragma optimize(2)
#define endl '\n'
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;
typedef long long ll;
typedef pair<int,int>PII; 
typedef unsigned long long ull;
const int M=2010;
const ll  llinf=0x3f3f3f3f3f3f3f3f;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int N=2e6+10;
int dx[4]={0,1,0,-1};
int dy[4]={-1,0,1,0};
void solve()
{
       int x1,y1,x2,y2,x3,y3;
       cin>>x1>>y1>>x2>>y2>>x3>>y3;
       if(y1==y2&&y1>y3)
       {
               long double len=abs(x2-x1);
               cout<<fixed<<setprecision(10)<<len<<endl;
       }
       else if(y1==y3&&y1>y2)
       {
               long double len=abs(x1-x3);
               cout<<fixed<<setprecision(10)<<len<<endl;
       }
       else if(y2==y3&&y2>y1)
       {
               long double len=abs(x2-x3);
               cout<<fixed<<setprecision(10)<<len<<endl;
       }else cout<<"0"<<endl;
       return ;
}
int main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
     //   freopen("test.in","r",stdin);
        int t;cin>>t;
        while(t--)solve();
        return 0;
}

B. Power Walking

思路：
莽夫题.尽可能把同一种东西分给同一种人即可.观察样例发现存在一种输出贪心输出方式.
即:$1\leq k \leq type $(最初的总的种类)时,都输出$type$
$k\geq type$,输出$k$即可。

AC Code：

#include<bits/stdc++.h>
#pragma optimize(2)
#define endl '\n'
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;
typedef long long ll;
typedef pair<int,int>PII; 
typedef unsigned long long ull;
const int M=2010;
const ll  llinf=0x3f3f3f3f3f3f3f3f;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int N=2e6+10;
int dx[4]={0,1,0,-1};
int dy[4]={-1,0,1,0};
void solve()
{ 
     int type=0;
     map<int,bool>mp;
     int n;cin>>n;
     for(int i=1;i<=n;i++)
     {
             int x;cin>>x;
             if(!mp[x])type++,mp[x]=true;
     }
     for(int i=1;i<=type;i++)cout<<type<<' ';
     for(int i=type+1;i<=n;i++)cout<<i<<' ';
     cout<<endl;
     return ;
}
int main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
      //  freopen("test.in","r",stdin);
        int t;cin>>t;
        while(t--)solve();
        return 0;
}

C. Great Sequence

思路：
排序一遍.从小到大贪心即可。
唯一问题:一定要开$long long$

AC Code：

#include<bits/stdc++.h>
#pragma optimize(2)
#define endl '\n'
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;
typedef long long ll;
typedef pair<int,int>PII; 
typedef unsigned long long ull;
const int M=2010;
const ll  llinf=0x3f3f3f3f3f3f3f3f;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int N=2e6+10;
int dx[4]={0,1,0,-1};
int dy[4]={-1,0,1,0};
void solve()
{
       int n,x;
       cin>>n>>x;
       vector<int>a(n+1);
       map<ll,int>mp;
       for(int i=1;i<=n;i++)cin>>a[i],mp[a[i]]++;
       sort(a.begin()+1,a.end());//升序
       int ans=0;
       for(int i=1;i<=n;i++)
       {
              if(mp[a[i]])//假如这样的数还存在只能往后匹配 
              {
                      if(mp[(ll)a[i]*x])mp[(ll)a[i]*x]--,mp[a[i]]--;
                      else ans++,mp[a[i]]--;
              }
       }
       cout<<ans<<endl;
       return ;
}
int main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
     //   freopen("test.in","r",stdin);
        int t;cin>>t;
        while(t--)solve();
        return 0;
}

D. Repetitions Decoding

思路:
如果某个数出现奇数次.一定无法构造:因为每次操作只能加一对数进去,因而无法使没有配对的变成能配对的.
但是可能出现偶数个出现奇数次的数,因此需要判断是否每个数都有配对.

此后给出结论:

• 只要满足上述条件即最开始的时候都是配对的那么一定能构造出来.

构造方式如下:
假定为 1 2 2 3 1 3
1 2 2 3 1 3 找到第一对1 1
将它们中间的数按如下方式插入:
1 2 2 3 1
1 2 2 3 1 2 2
1 2 2 3 1 2 2 2 2
1 2 2 3 1 2 2 3 3 2 2.每次都把1 1中间还没有操作过的往右侧的中间插进去。
此时左侧 1 2 2 3 1 2 2 3就是一个 repeat sequence 而新假如的 2 2 3 3 2 2 一半和左侧构成repeat sequence消掉1 1 右侧就是原来中间的反串.即2 2 3在消掉1 1后以反串的形式出现在 右侧了.
即[1 2 2 3 1 2 2 3] 3 2 2 3.
由于至多有n/2对因此操作n/2次后即可构造完毕.

AC Code:

#include<bits/stdc++.h>
#pragma optimize(2)
#define endl '\n'
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;
typedef long long ll;
typedef pair<int,int>PII; 
typedef unsigned long long ull;
const int M=2010;
const ll  llinf=0x3f3f3f3f3f3f3f3f;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int N=2e6+10;
int dx[4]={0,1,0,-1};
int dy[4]={-1,0,1,0};
bool vis[510];//500个位置 
struct node{
        ll pos,c;
};
void solve()
{
       memset(vis,false,sizeof vis);//最初全没有处理 
       int n;cin>>n;
       vector<ll>a(n+1);
       unordered_map<ll,ll>mp;
       for(int i=1;i<=n;i++)cin>>a[i],mp[a[i]]++;
       bool ok=true;
       for(auto c:mp)
        if(c.second%2!=0)
        {
                ok=false;
                break;
        }
       if(!ok||n%2!=0)cout<<"-1"<<endl;//有数出现奇数次或者长度为奇数 
       else
       {
               vector<node>op;
               vector<int>split;//分组情况 
               int sum=0;//左侧已经累积了多少东西 
               for(int i=1;i<=n;i++)
                if(!vis[i])
                {
                        int r;
                        int tmp=1;//统计[l,r]有多少数 
                        for(int j=i+1;j<=n;j++)
                         if(!vis[j])
                         {
                                 tmp++;
                                 if(a[j]==a[i])
                                 {
                                         r=j;
                                         break;//找到右边界 
                                 }
                         }
                        vis[i]=true,vis[r]=true;//删掉两个已经消掉的点 
                        int res=0;


                        for(int j=i+1;j<=r;j++)
                         if(!vis[j])//假如说这个点是没有被消掉的 
                         {
                                 op.push_back({sum+tmp+res,a[j]});//插入后面 
                                 res++;
                         }
                        sum+=tmp*2-2;
                        split.push_back(tmp*2-2);  

                        vector<int>b;
                        for(int j=i+1;j<=r-1;j++)
                         if(!vis[j])b.push_back(a[j]); 
                        reverse(b.begin(),b.end());
                        int cnt=0;
                        for(int j=i+1;j<=r-1;j++)
                         if(!vis[j])a[j]=b[cnt++];                  
                }
              cout<<op.size()<<endl;
               for(auto res:op)cout<<res.pos<<' '<<res.c<<endl;
               cout<<split.size()<<endl;
               for(auto c:split)cout<<c<<' ';
               cout<<endl;
       }
       return ;
}
//[1 2 2 3 1 2 2 3] 3 2 2 3

int main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
      //  freopen("test.in","r",stdin);
        int t;cin>>t;
        while(t--)solve();
        return 0;
}