高斯消元 & 求组合数

高斯消元 —— 模板题 AcWing 883. 高斯消元解线性方程组

• 用代码实现对增广矩阵的系数部分进行初等行变换
• 步骤
  • 枚举每一列 $c$
    1.找到该列绝对值最大的数所在的行
    2.将该行换到最上面未被固定的行
    3.将改行所有数乘以枚举到的数的倒数
    4.将第 $c$ 列的所有数消成 $0$
    5.固定该行
    6.如果下一列是矩阵最后一列，则反向枚举，并用该行唯一的非 $0$ 元消去该列所有元素，直到系数部分是单位阵；若不是最后一行，则继续枚举

模板

// a[N][N]是增广矩阵
int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )   // 找到绝对值最大的行
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);      // 将绝对值最大的行换到最顶端
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];      // 将当前行的首位变成1
        for (int i = r + 1; i < n; i ++ )       // 用当前行将下面所有的列消成0
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; // 无解
        return 1; // 有无穷多组解
    }

    for (int i = n - 1; i >= 0; i -- )      
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];

    //个人认为这三行代码的思路并不是y总上课演示的思路。
    //i从下往上枚举的是所有解。要把a[i][n]变成解，需要第i行除a[i][i] 外所有数均为0.
    //经过上面的计算，已经保证第i行a[i][i]之前的所有数均为0，a[i][i] == 1，第i行以下的所有行中只有对角线上元素非0
    //j > i,因此a[i][j] 所在的第j列只有a[j][j]非0；要消掉a[i][j],需要a[i][j] -= a[j][j] * a[i][j]
    //此时a[i][n]的变化就是 a[i][n] -= a[i][j] * a[j][n]
    //因此这段代码可以保证得出答案

    return 0; // 有唯一解
}

//输出时可能会输出-0.00,要转化一下

• 代码

求组合数

• 直接计算，时间复杂度很大，会超时。优化关键在于预处理
• 注解：下面的数据范围中，$n$ 表示询问次数，$a b$ 表示组合数上下标，$p$ 表示取模的数

递推法求组合数 —— 模板题 AcWing 885. 求组合数 I

• 数据范围：$$1≤n≤10000$$ $$1≤b≤a≤2000$$
• 关键等式：$$C^{b}_{a}=C^{b}_{a-1}+C^{b-1}_{a-1}$$ 说明：从 $a$ 个苹果里选出 $b$ 个苹果，相当于从 $a-1$ 个苹果中选 $b$ 个苹果，或从 $a-1$ 个苹果中选 $b-1$ 个苹果，让剩下的那个苹果成为第 $b$ 个苹果
• 通过上述递推式先预处理出所有组合数，询问时直接查询数组即可

时间复杂度：$O(ab)$

模板

// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
    for (int j = 0; j <= i; j ++ )
        if (!j) c[i][j] = 1;
        else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

• 代码

通过预处理逆元的方式求组合数 —— 模板题 AcWing 886. 求组合数 II

• 数据范围：$$1≤n≤10000$$ $$1≤b≤a≤10^5$$
• 注意，这里的题数据范围比上一题要大得多，因此上一题的算法在这一题会超时

时间复杂度：$O(a\log 10^{9})$

模板

首先预处理出所有阶乘取模的余数fact[N]，以及所有阶乘取模的逆元infact[N]
如果取模的数是质数，可以用费马小定理求逆元
int qmi(int a, int k, int p)    // 快速幂模板
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
    fact[i] = (LL)fact[i - 1] * i % mod;
    infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}

• 代码

Lucas定理 —— 模板题 AcWing 887. 求组合数 III

• 数据范围：$$1≤n≤20$$ $$1≤b≤a≤10^{18}$$
• 这里的数据又爆空间又爆时间。可以用卢卡斯定理来优化预处理
• 卢卡斯定理：$$C^{a}_{b}\equiv C^{a\bmod p}_{b\bmod p}\times C^{a/p}_{b/p}\pmod p$$ (p为质数)
  • 证明：$a b$ 分别转化成 $p$ 进制再转化会十进制可以得到算式：$$a=a_{k}p^{k}+a_{k-1}p^{k-1}+…+a_{0}·p^{0}$$ $$b=b_{k}p^{k}+b_{k-1}p^{k-1}+…+b_{0}·p^{0}$$
  • 因此 $$(1+x)^{a}=(1+x)^{a_0}((1+x)^{p})^{a_1}…((1+x)^{p^{k}})^{a_k}$$
  • 因为 $$(1+x)^{p}=C^{0}_{p}1+C^{1}_{p}x+…+C^{p}_{p}x^{p}\equiv 1+x^{p}\pmod p$$
    • 由数学归纳法，可以得出 $$(1+x)^{p^{k}}\equiv 1+x^{p^{k}}\pmod p$$
  • 所以 $$(1+x)^{a}\equiv (1+x)^{a_0}(1+x^{p})^{a_1}…(1+x^{p^{k}})^{a_k}\pmod p$$ 对比等式两边 $x^{b}$ 的系数可知 $$C^{b}_{a}\equiv C^{b_0}_{a_0}C^{b_1}_{a_1}…C^{b_{k}}_{a_{k}}\pmod p$$
  • 以上是对应y总讲课里面的算式证明。对于本blog里卢卡斯定理的形式的证明，可以参考这篇博客

时间复杂度：$$O(\log_{p}a\times p\log p)=O(p\log a)$$ $\log_{p}a$ 是求 $a\bmod p$ 和 $b\bmod p$ 的时间，因为 $a b$ 转化成 $p$ 进制都是 $\log_{p}a$ 位

模板

若p是质数，则对于任意整数 1 <= m <= n，有：
    C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)

int qmi(int a, int k, int p)  // 快速幂模板
{
    int res = 1 % p;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b, int p)  // 通过定理求组合数C(a, b)
{
    if (a < b) return 0;

    LL x = 1, y = 1;  // x是分子，y是分母
    for (int i = a, j = 1; j <= b; i --, j ++ )
    {
        x = (LL)x * i % p;
        y = (LL) y * j % p;
    }

    return x * (LL)qmi(y, p - 2, p) % p;
}

int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

• 代码

分解质因数法求组合数 —— 模板题 AcWing 888. 求组合数 IV

• 数据范围：$$1≤b≤a≤5000$$
• 从定义出发求组合数，结果可能很大，需要高精度
• 如果高精度乘法和高精度除法都实现的话运行效率会比较低。因此先分解质因数，计算时只用到高精度乘法即可
• 组合数：$$C^{a}_{b}=\frac{a\times (a-1)\times …(a-b+1)}{b\times (b-1)\times …1}=\frac{a!}{b!(a-b)!}$$
  • 为了方便分解质因数，我们用带阶乘的算式来做
  • 对一个阶乘数分解质因数：$$a!=p_{1}^{\alpha _1}p_{2}^{\alpha _2}…p_{k}^{\alpha _k}$$ 如何求出 $p_{i}$ 对应的指数 $\alpha _{i}$ 呢 $$\alpha _{i}=\lfloor \frac{a}{p_i} \rfloor +\lfloor \frac{a}{p_i^{2}} \rfloor +\lfloor \frac{a}{p_i^{3}} \rfloor +…$$

模板

当我们需要求出组合数的真实值，而非对某个数的余数时，分解质因数的方式比较好用：
    1. 筛法求出范围内的所有质数
    2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
    3. 用高精度乘法将所有质因子相乘

int primes[N], cnt;     // 存储所有质数
int sum[N];     // 存储每个质数的次数
bool st[N];     // 存储每个数是否已被筛掉


void get_primes(int n)      // 线性筛法求素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)       // 求n！中的次数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)       // 高精度乘低精度模板
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }

    while (t)                       
    {
        c.push_back(t % 10);
        t /= 10;
    }
    //这里的t可能是两位以上的数，不能直接将t放进数组中
    //因为该数组要被反复的乘，存t的那一位可能会溢出而导致答案错误
    //因此t要进一步被分解，数组中每一个元素都要保证是个位数
    //在高精度乘法模板题中，由于高精度乘法只执行一次，不存在数组中某一位溢出的问题，就不需要对t进行细分处理

    return c;
}

get_primes(a);  // 预处理范围内的所有质数

for (int i = 0; i < cnt; i ++ )     // 求每个质因数的次数
{
    int p = primes[i];
    sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}

vector<int> res;
res.push_back(1);

for (int i = 0; i < cnt; i ++ )     // 用高精度乘法将所有质因子相乘
    for (int j = 0; j < sum[i]; j ++ )
        res = mul(res, primes[i]);

• 代码

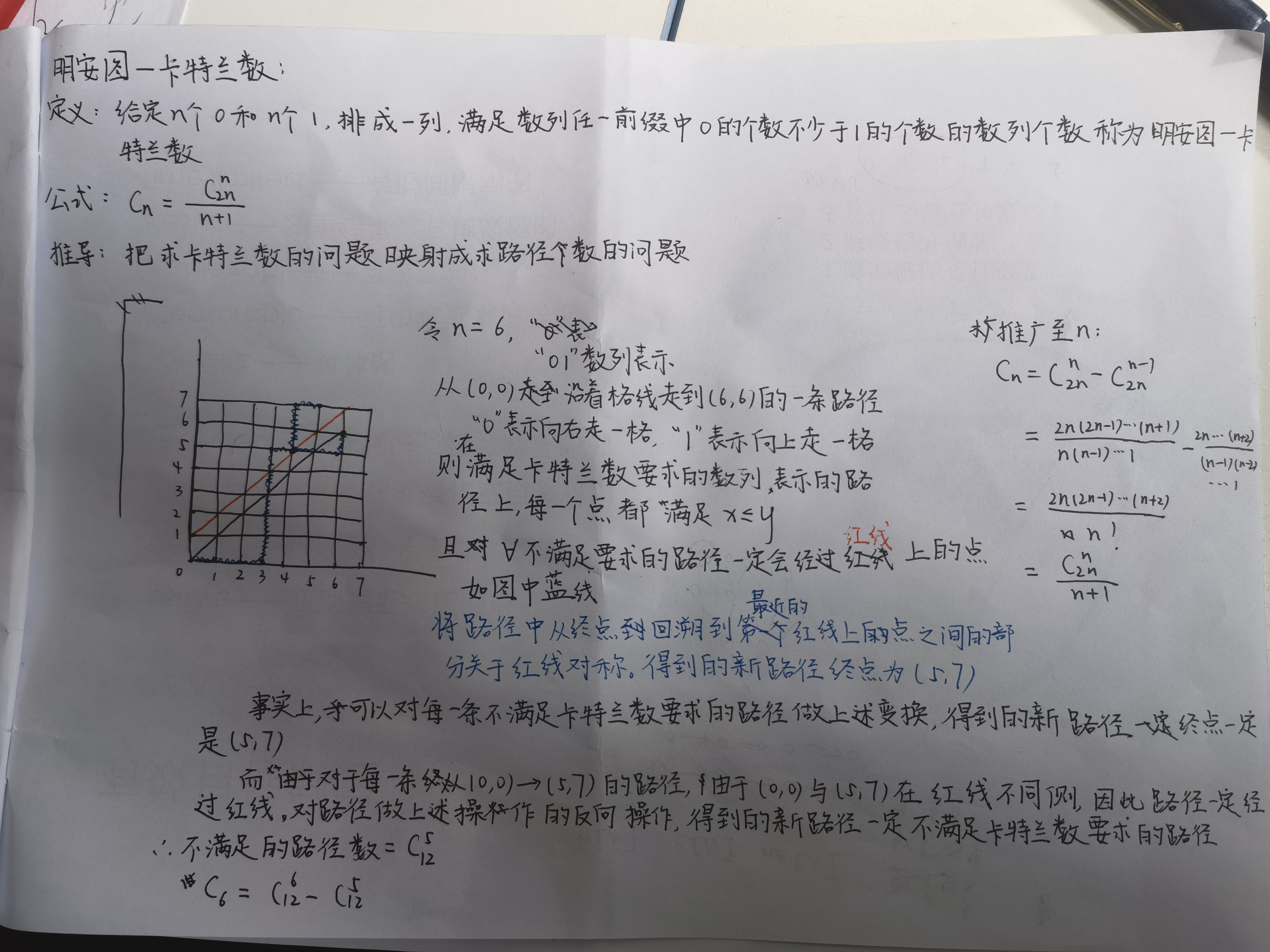
卡特兰数 —— 模板题 AcWing 889. 满足条件的01序列

模板

给定n个0和n个1，它们按照某种顺序排成长度为2n的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为： Cat(n) = C(2n, n) / (n + 1)

• 代码

作者：yxc
链接：https://www.acwing.com/blog/content/406/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。