线性代数

向量表示

从 物理学 角度说，向量 是一个有固定长度和方向的箭头

从 计算机科学 角度来说，向量 是一个形如 $a = [x, y, z]$ 的数字列表

但事实上，向量最好的理解方式是：

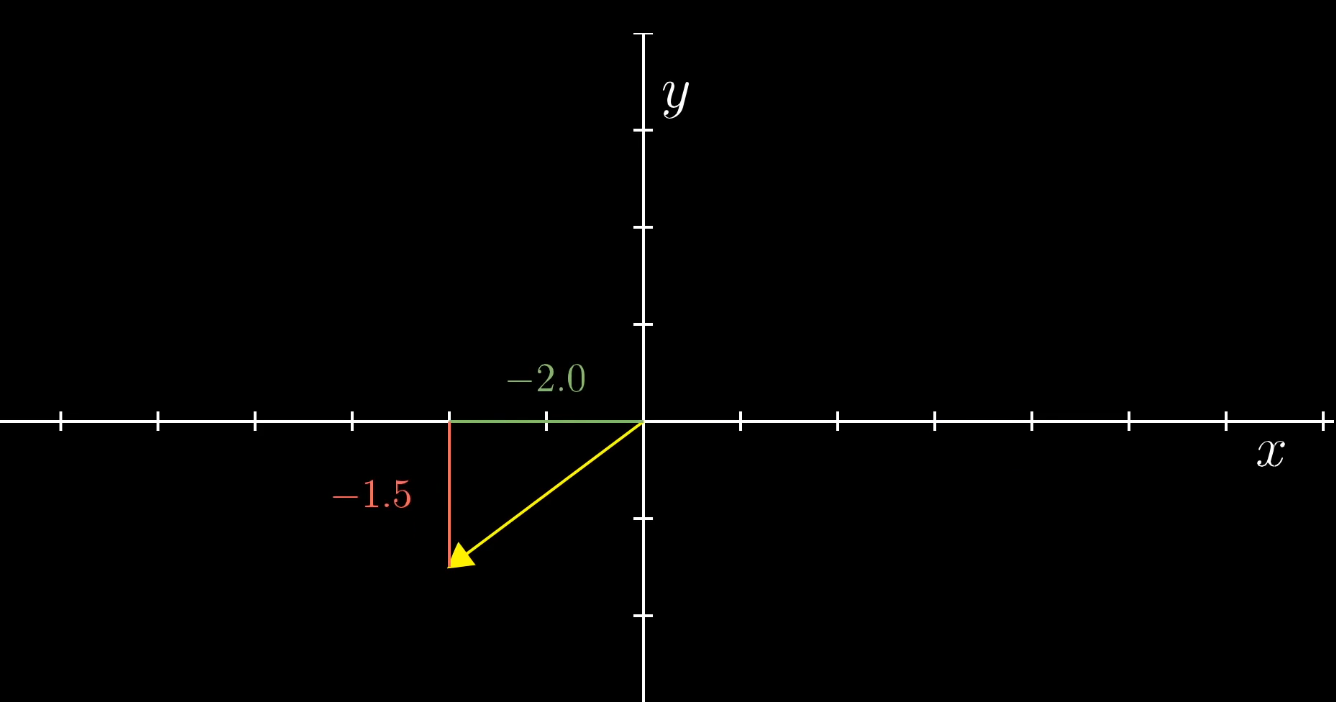
建立坐标系，用物理的箭头来表示，同时用数字列表 记录 向量的坐标值，

需要注意的是，所有向量图示都将 原点 $O$ 表示为 $[0…0]$。

但是，向量 并不是一成不变的，它同样支持如 加减乘除开方 等运算。

向量的加减法

与小学中我们所学到的 数轴上加减法 理解上无异，但可能 扩展到 多维。

我们将 一个向量的终点 看作是 下一个向量的起点，则最后的值等于 从原点到最后一个向量的终点。

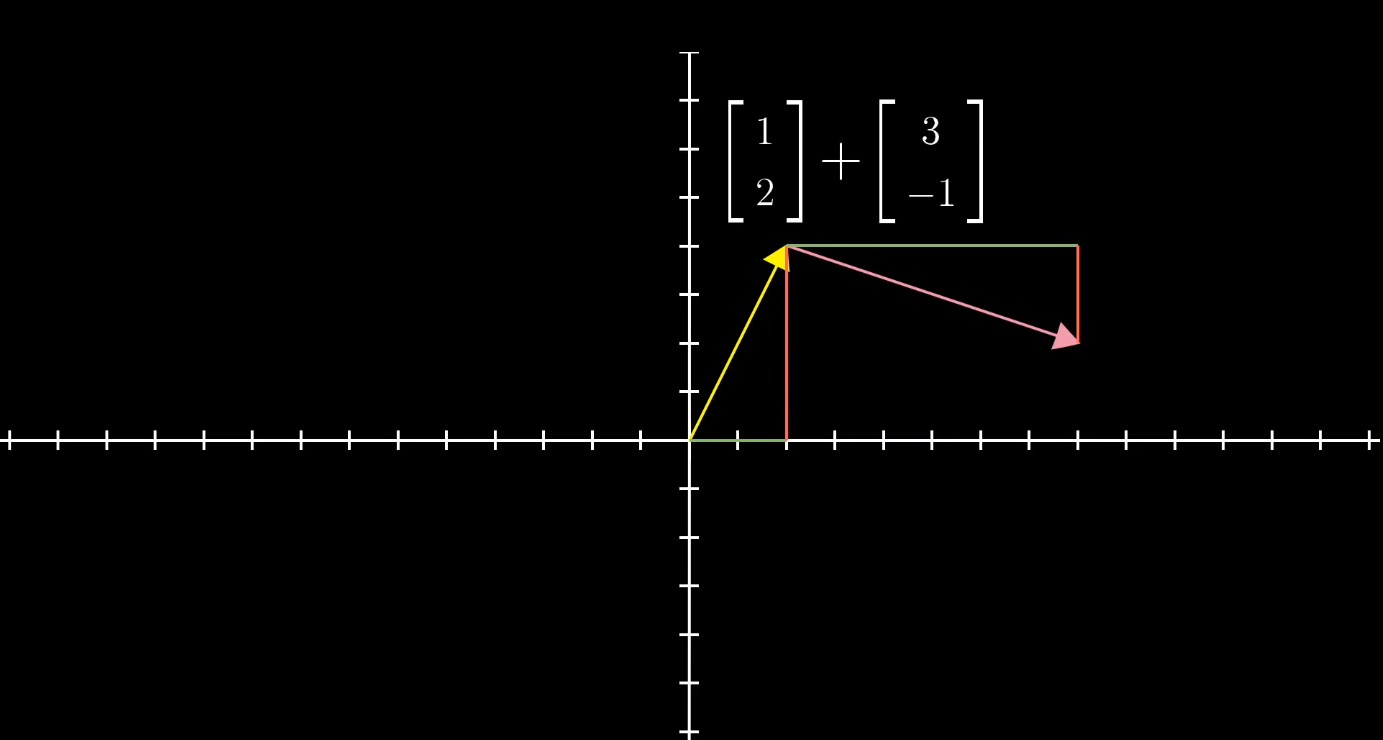
如图所示，答案为 $[4, 1]$，即为粉色向量的终点。

总结来说，就是将 对应项 的值相加或相减

向量的乘除法

乘法 即将一个向量的长度 缩放，开方操作 同理

除法 则可以理解为 从原点反向 做乘法操作，

值得一提的是，这些影响向量的数字也可以称为 标量

扩展延伸

线性代数 可以清晰表达大量 不同数据 ，

更重要的是能 直观地 对空间不同变化进行描绘。