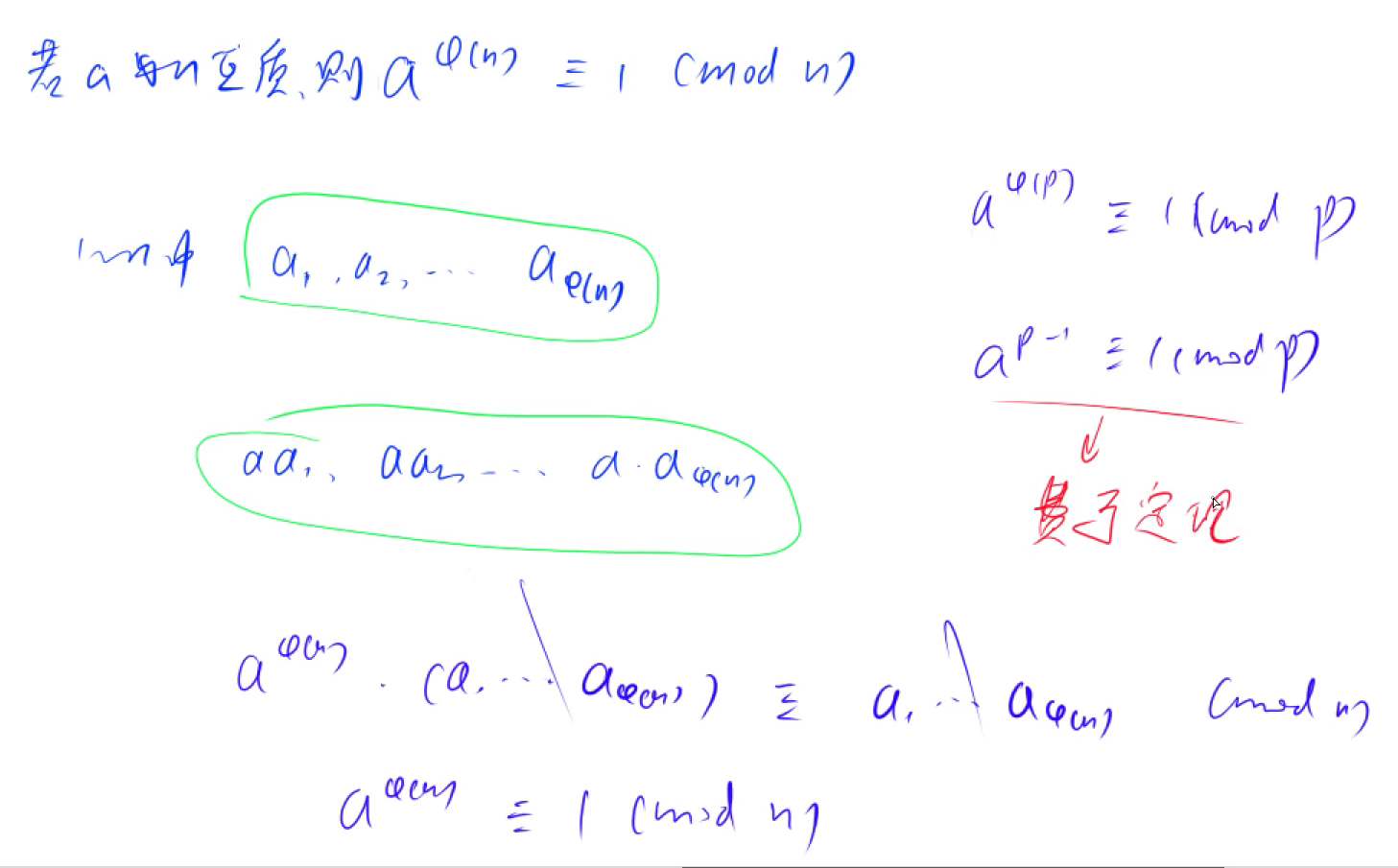
先找出1到n之间与n互质的数

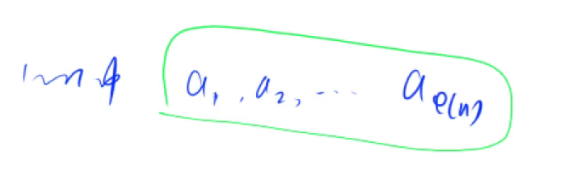
然后因为a与n互质，所以1到n与n互质的数的乘积也与n互质，所以在第一组的每个数都乘上a后也就是第二组数是和第一组数是一样的，这里肯定会有很多人问，第二组数不是每个数都在第一组数的基础上都乘上了a吗?
其实这两组数并不是真正意义上的数值相等，而是第二组数在乘a后mod n之后就是原来第一组的数，这里又会问这里对n取模之后为什么会和原来的数一样只不过是顺序不同
这是因为首先对mod n的余数肯定不会超过n(也不会等于n)也就是第二组的每个数都在0到n - 1的范围内，然后第二组的每个数其实都等于kn + q(k为商，q为余数)如果q不和n互质的话那么kn + q就不会和n互质，和第二组都和n互质矛盾了，所以得出的余数q肯定和n互质，q又在0 到 n - 1的范围内，第二组的数目和第一组相同，且两两不同，所以肯定第二组的数mod n之后是和第一组一样的只不过是顺序可能不同

所以两组数每个数的乘积mod n的余数是一样的

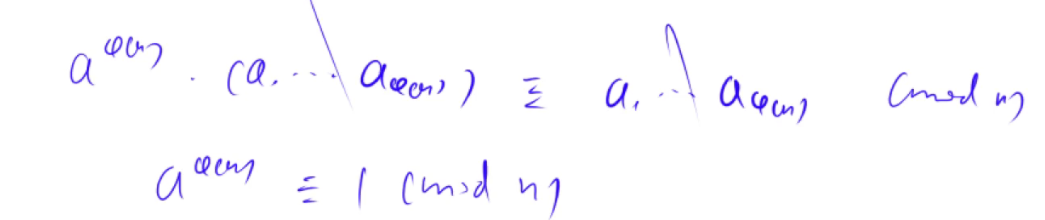
而第二组数据两两不同以及最后为什么第一组数值的所有乘积为与n互质的数就能够约掉
其实是借助了剩余系定理三

而(m,c) = 1是表示m和c是互质的，个人理解(c, m) = 0应该是表示的是m = 0的情况下而将式子变形为最后一步时
两个数相乘的结果可以被n整除，其中一个数又与n是互质的，所以一定是另外一个数可以被n整除
举个例子5 * 6 = 0 mod 35和3互质，两边同时除以5就是6 = 0 mod 3还是对的
有一种更好的理解就是借助最基本的同于关系的性质

因此由以上可以证明欧拉定理，而费马小定理其实时采用了p为质数时和p在1到p中有p - 1个互质的数来证明的