这几天整理了莫队算法,关于莫队,很多参考书和参考资料缺少详细的描述
《算法竞赛进阶指南》中也很少有莫队算法相关的内容
这里做一个补充
内容有点多,我在自己博客上也写了相关内容
嵌套与分块数据结构(一)
嵌套与分块数据结构(二)
莫队综合题
莫队算法模版
莫队算法的核心,是对大量的询问进行处理。
每个询问一般都有一个区间[l, r],我们对询问进行分块
分块过程
bool cmp(const Qry& a, const Qry& b) {
if(belong[a.l] ^ belong[b.l]) return belong[a.l] < belong[b.l];
if(belong[a.l] & 1) return a.r < b.r;
return a.r > b.r;
}
void block() {
sz = sqrt(1.0 * n);
t = n / sz;
_rep(i, 1, t) _rep(k, (i - 1) * sz + 1, i * sz) {
belong[k] = i;
}
if(t * sz < n) {
t++;
_rep(k, (t - 1) * sz + 1, n) belong[k] = t;
}
}
主过程
inline void add(int x, int& ans) {
if(++num[x] == 1) ans++;
}
inline void del(int x, int& ans) {
if(--num[x] == 0) ans--;
}
void solve() {
sort(qry + 1, qry + 1 + m, cmp);
Set(num, 0);
tans = 0;
int l = 1, r = 0;
_rep(i, 1, m) {
while (l < qry[i].l) del(A[l++], tans);
while (l > qry[i].l) add(A[--l], tans);
while (r < qry[i].r) add(A[++r], tans);
while (r > qry[i].r) del(A[r--], tans);
ANS[qry[i].id] = tans;
}
}
结合代码思考,这就是“大段维护,不完整段局部朴素”的思想

编程技巧
int l = 1, r = 0;
while (l < ql) // ...
while (r < qr) // ...
假设询问区间是[ql, qr]
我们令l = 1, r = 0为初始值
然后扩展到[ql, qr],看相关变化
离线莫队算法
参考代码如下
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <sstream>
#include <iomanip>
#include <cmath>
#include <bitset>
#include <assert.h>
using namespace std;
typedef long long llong;
typedef set<int>::iterator ssii;
#define Cmp(a, b) memcmp(a, b, sizeof(b))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define Set(a, v) memset(a, v, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define _forS(i, l, r) for(set<int>::iterator i = (l); i != (r); i++)
#define _rep(i, l, r) for(int i = (l); i <= (r); i++)
#define _for(i, l, r) for(int i = (l); i < (r); i++)
#define _forDown(i, l, r) for(int i = (l); i >= r; i--)
#define debug_(ch, i) printf(#ch"[%d]: %d\n", i, ch[i])
#define debug_m(mp, p) printf(#mp"[%d]: %d\n", p->first, p->second)
#define debugS(str) cout << "dbg: " << str << endl;
#define debugArr(arr, x, y) _for(i, 0, x) { _for(j, 0, y) printf("%c", arr[i][j]); printf("\n"); }
#define _forPlus(i, l, d, r) for(int i = (l); i + d < (r); i++)
#define lowbit(i) (i & (-i))
#define MPR(a, b) make_pair(a, b)
const int maxn = 50000 + 10;
int n, m, A[maxn];
// == block ==
int belong[maxn], sz, t;
void block() {
sz = sqrt(n);
t = n / sz;
_rep(i, 1, t) {
_rep(k, (i - 1) * sz + 1, i * sz) belong[k] = i;
}
if(t * sz < n) {
t++;
_rep(k, (t - 1) * sz + 1, n) belong[k] = t;
}
}
// == block finished ==
inline llong gcd(llong a, llong b) {
return b ? gcd(b, a % b) : a;
}
// == query structure ==
class Qry {
public:
int l, r;
int id;
};
Qry qry[maxn];
int cmp(const Qry& a, const Qry& b) {
if(belong[a.l] ^ belong[b.l]) return belong[a.l] < belong[b.l];
if(belong[a.l] & 1) return a.r < b.r;
return a.r > b.r;
}
// == query finished ==
// == Mo's algotithm ==
llong num[maxn];
void maintain(int x, int d, llong& ans) {
ans -= num[x] * (num[x] - 1);
num[x] += d;
ans += num[x] * (num[x] - 1);
}
llong ANS[maxn][2];
void solve() {
int l = 1, r = 0;
llong res = 0;
_rep(i, 1, m) {
int ql = qry[i].l, qr = qry[i].r;
if(ql == qr) {
ANS[qry[i].id][0] = 0;
ANS[qry[i].id][1] = 1;
continue;
}
while (l < ql) maintain(A[l++], -1, res);
while (l > ql) maintain(A[--l], 1, res);
while (r < qr) maintain(A[++r], 1, res);
while (r > qr) maintain(A[r--], -1, res);
llong D = (llong)(qry[i].r - qry[i].l + 1) * (qry[i].r - qry[i].l);
llong g = gcd(D, res);
ANS[qry[i].id][0] = res;
ANS[qry[i].id][1] = D;
if(!g) ANS[qry[i].id][1] = 1;
else {
ANS[qry[i].id][0] /= g;
ANS[qry[i].id][1] /= g;
}
}
}
// == Mo finished ==
void init() {
Set(num, 0);
Set(ANS, 0);
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
init();
// == get input ==
scanf("%d%d", &n, &m);
_rep(i, 1, n) scanf("%d", &A[i]);
_rep(i, 1, m) {
scanf("%d%d", &qry[i].l, &qry[i].r);
qry[i].id = i;
}
// == input finished ==
// == block ==
block();
// == block finsihed ==
// == solve the problem ==
sort(qry + 1, qry + 1 + m, cmp);
solve();
_rep(i, 1, m) printf("%lld/%lld\n", ANS[i][0], ANS[i][1]);
}
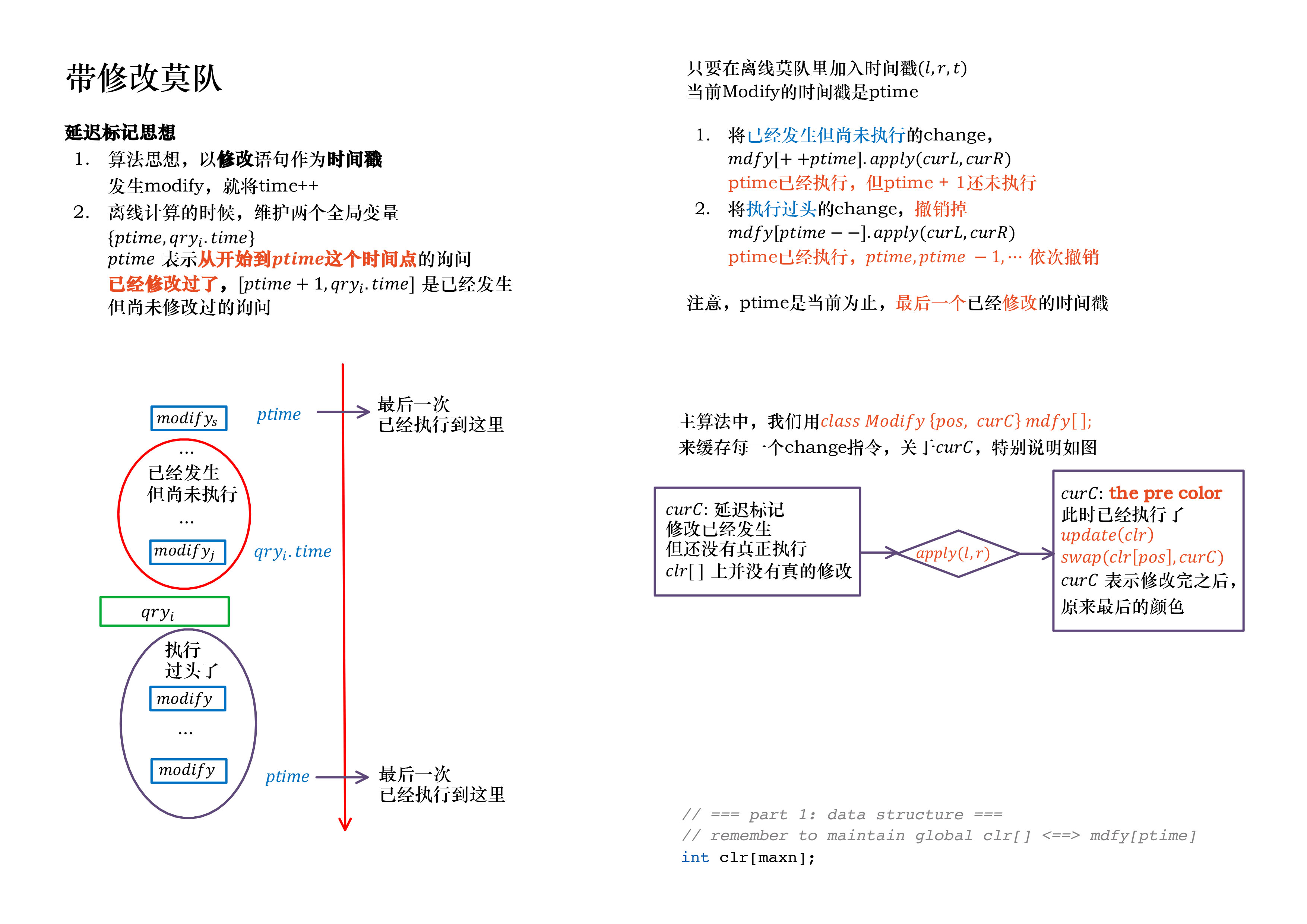
带修改莫队
const int maxn = 1000000 + 5;
int n, m, t, sz;
int CNT[maxn];
int clr[maxn];
int cntq = 0, cntc = 0;
int ANS[maxn];
void init() {
cntq = cntc = 0;
}
class Query {
public:
int l, r, id, time;
};
Query qry[maxn];
inline void add(int x, int& ans) {
if(++CNT[x] == 1) ans++;
}
inline void del(int x, int& ans) {
if(--CNT[x] == 0) ans--;
}
// == init block ==
int tans = 0;
void initBlk() {
tans = 0;
}
// == init block finished ==
class Modify {
public:
int pos, curC;
void apply(int curL, int curR) {
if(curL <= pos && pos <= curR) {
int oldC = clr[pos];
del(oldC, tans);
add(curC, tans);
}
swap(curC, clr[pos]);
}
};
Modify mdfy[maxn];
// === block() by n ===
int belong[maxn];
void block() {
Set(belong, 0);
sz = pow(n, 2.0 / 3.0);
t = n / sz;
_rep(i, 1, t) {
_rep(k, (i - 1) * sz + 1, i * sz) belong[k] = i;
}
if(t * sz < n) {
t++;
_rep(k, (t - 1) * sz + 1, n) belong[k] = t;
}
// debug(t);
}
// == solve() ==
bool cmp(const Query& a, const Query& b) {
if(belong[a.l] ^ belong[b.l]) return belong[a.l] < belong[b.l];
if(belong[a.r] ^ belong[b.r]) return belong[a.r] < belong[b.r];
return a.time < b.time;
}
void solve() {
sort(qry + 1, qry + 1 + cntq, cmp);
initBlk();
assert(tans == 0);
// get started ptime and [l, r]
int ptime = 0, l = 0, r = 0;
// then expand to other query by recursion
_rep(i, 1, cntq) {
int ql = qry[i].l, qr = qry[i].r, qt = qry[i].time;
while (l < ql) del(clr[l++], tans);
while (l > ql) add(clr[--l], tans);
while (r < qr) add(clr[++r], tans);
while (r > qr) del(clr[r--], tans);
while (ptime < qt) mdfy[++ptime].apply(l, r);
while (ptime > qt) mdfy[ptime--].apply(l, r);
ANS[qry[i].id] = tans;
//debug(clr[1]);
}
}
// == solve fnished ==
// === block() finished ===
int main() {
freopen("input.txt", "r", stdin);
init();
// == input ==
scanf("%d%d", &n, &m);
_rep(i, 1, n) {
scanf("%d", &clr[i]);
}
assert(cntq == 0 && cntc == 0);
_rep(i, 1, m) {
char op[2];
scanf("%s", op);
if(op[0] == 'Q') {
Query& curq = qry[++cntq];
scanf("%d%d", &curq.l, &curq.r);
curq.id = cntq;
curq.time = cntc;
//debug(curq.time);
}
else {
Modify& md = mdfy[++cntc];
scanf("%d%d", &md.pos, &md.curC);
// mdfy[] as a tag, we not really change here
}
}
// == input finished ==
// == block ==
block();
// == block finished ==
solve();
_rep(i, 1, cntq) printf("%d\n", ANS[i]);
}
莫队算法的典型问题–区间众数(复杂版)

const int maxn = 40000 + 10;
const int maxt = 35 + 5;
class Mode {
public:
int CNT, pos;
void clear() {
CNT = pos = 0;
}
};
Mode f[maxt][maxt], cur;
int belong[maxn], c[maxt][maxt][maxn];
void init() {
Set(belong, 0);
Set(c, 0);
}
int a[maxn], buf[maxn];
int n, m, tot, t, sz;
void discrete() {
Cpy(buf, a);
sort(buf + 1, buf + 1 + n);
tot = unique(buf + 1, buf + 1 + n) - buf - 1;
_rep(i, 1, n) {
a[i] = lower_bound(buf + 1, buf + 1 + tot, a[i]) - buf;
}
}
// == block ==
class Blk {
public:
int L, R;
};
Blk blk[maxn];
void block() {
t = pow((double)n, 1.0 / 3.0);
sz = t ? n / t : n;
_rep(i, 1, t) {
blk[i].L = (i - 1) * sz + 1;
blk[i].R = i * sz;
}
if(blk[t].R < n) {
t++;
blk[t].L = blk[t - 1].R + 1;
blk[t].R = n;
}
_rep(i, 1, t) _rep(k, blk[i].L, blk[i].R) {
belong[k] = i;
}
}
// == blocked finished ==
// == init seg ==
void initseg() {
cur.clear();
_for(i, 0, maxt) _for(j, 0, maxt) f[i][j].clear();
_rep(i, 1, t) _rep(j, i, t) {
_rep(k, blk[i].L, blk[j].R) {
++c[i][j][a[k]];
}
_rep(x, 1, tot) {
if(f[i][j].CNT < c[i][j][x]) {
f[i][j].CNT = c[i][j][x];
f[i][j].pos = x;
}
}
}
}
// == init seg finished ==
inline void maintain(int x, int y, int val) {
++c[x][y][val];
if(c[x][y][val] > cur.CNT || (c[x][y][val] == cur.CNT && val < cur.pos)) {
cur.CNT = c[x][y][val];
cur.pos = val;
}
}
// == query ==
int query(int l, int r) {
int p = belong[l], q = belong[r];
int x = 0, y = 0;
if(p + 1 <= q - 1) {
x = p + 1; y = q - 1;
}
cur = f[x][y];
if(p == q) {
// at the same block
_rep(i, l, r) maintain(x, y, a[i]);
_rep(i, l, r) --c[x][y][a[i]];
}
else {
_rep(i, l, blk[p].R) maintain(x, y, a[i]);
_rep(i, blk[q].L, r) maintain(x, y, a[i]);
_rep(i, l, blk[p].R) --c[x][y][a[i]];
_rep(i, blk[q].L, r) --c[x][y][a[i]];
}
return buf[cur.pos];
}
// == query finished ==
int main() {
freopen("input.txt", "r", stdin);
init();
// == input ==
cin >> n >> m;
_rep(i, 1, n) scanf("%d", &a[i]);
// == input finished ==
// == discrete ==
discrete();
// == discrete finished ==
// == block ==
block();
// == block finished ==
// == then init Segment ==
initseg();
// == init segment finished ==
// == then solve() ==
int x = 0;
while (m--) {
int l, r;
scanf("%d%d", &l, &r);
l = (l + x - 1) % n + 1;
r = (r + x - 1) % n + 1;
if(l > r) swap(l, r);
x = query(l, r);
printf("%d\n", x);
}
}
莫队算法的典型问题–区间众数(简单版)

树上莫队
树上莫队背景知识
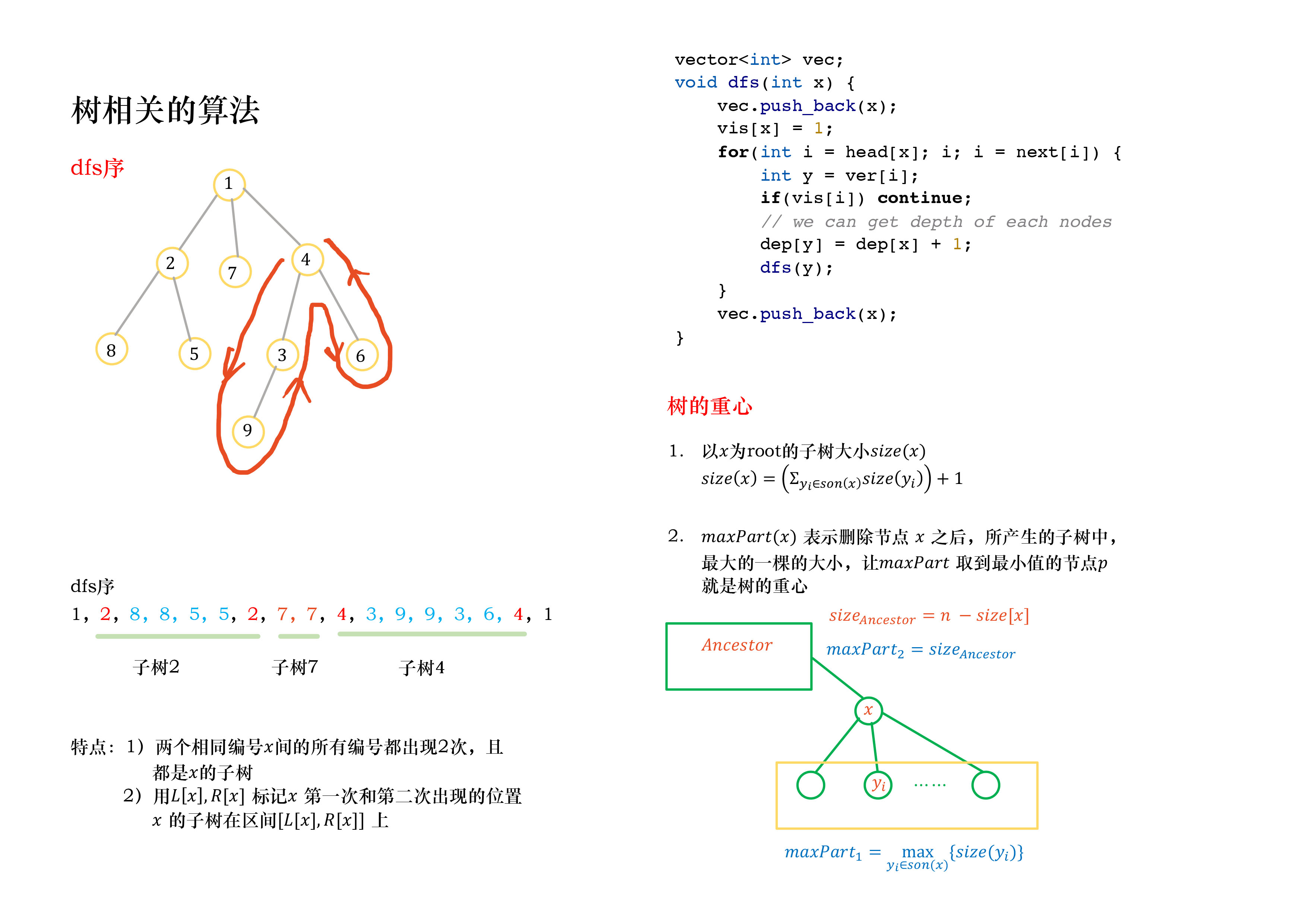


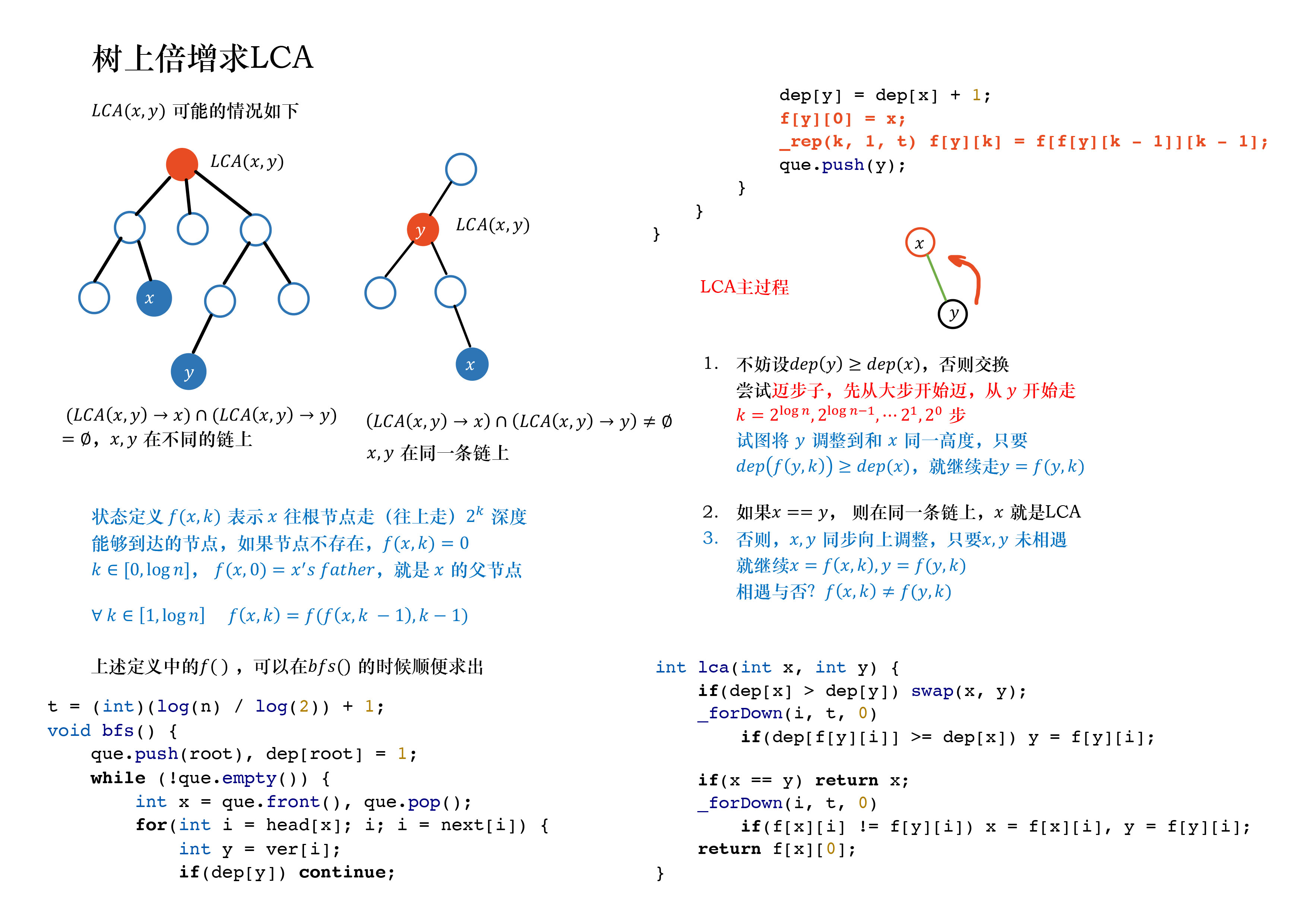
树上LCA
const int maxn = 50000 + 10;
const int maxt = 20;
int n, m, t;
int T;
// == lca init() ==
int f[maxn][maxt], dist[maxn], dep[maxn];
// == lca finished ==
// == graph ==
int head[maxn], ver[maxn * 2], nxt[maxn * 2], w[maxn * 2];
int tot = 0;
void init() {
Set(head, 0);
Set(ver, 0);
Set(nxt, 0);
Set(w, 0);
Set(f, 0);
Set(dist, 0);
Set(dep, 0);
tot = 0;
}
void add(int x, int y, int z) {
ver[++tot] = y, nxt[tot] = head[x], head[x] = tot;
w[tot] = z;
}
// == graph finished ==
// == init lca and bfs() ==
queue<int> que;
void bfs() {
t = (int)(log(n) / log(2)) + 1;
que.push(1), dep[1] = 1;
while (!que.empty()) {
int x = que.front(); que.pop();
for(int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if(dep[y]) continue;
dep[y] = dep[x] + 1;
f[y][0] = x;
dist[y] = dist[x] + w[i];
_rep(k, 1, t) f[y][k] = f[f[y][k - 1]][k - 1];
que.push(y);
}
}
}
// == bfs finished
// == lca ==
int lca(int x, int y) {
if(dep[x] > dep[y]) swap(x, y);
_forDown(k, t, 0) if(dep[f[y][k]] >= dep[x]) y = f[y][k];
if(x == y) return x;
_forDown(k, t, 0) if(f[x][k] != f[y][k]) {
x = f[x][k], y = f[y][k];
}
return f[x][0];
}
// == lca finished ==
int main() {
freopen("input.txt", "r", stdin);
scanf("%d", &T);
while (T--) {
init();
scanf("%d%d", &n, &m);
_for(i, 1, n) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(x, y, z);
add(y, x, z);
}
// == input finished ==
// bfs and lca
bfs();
_rep(i, 1, m) {
int x, y;
scanf("%d%d", &x, &y);
printf("%d\n", dist[x] + dist[y] - 2 * dist[lca(x, y)]);
}
}
}
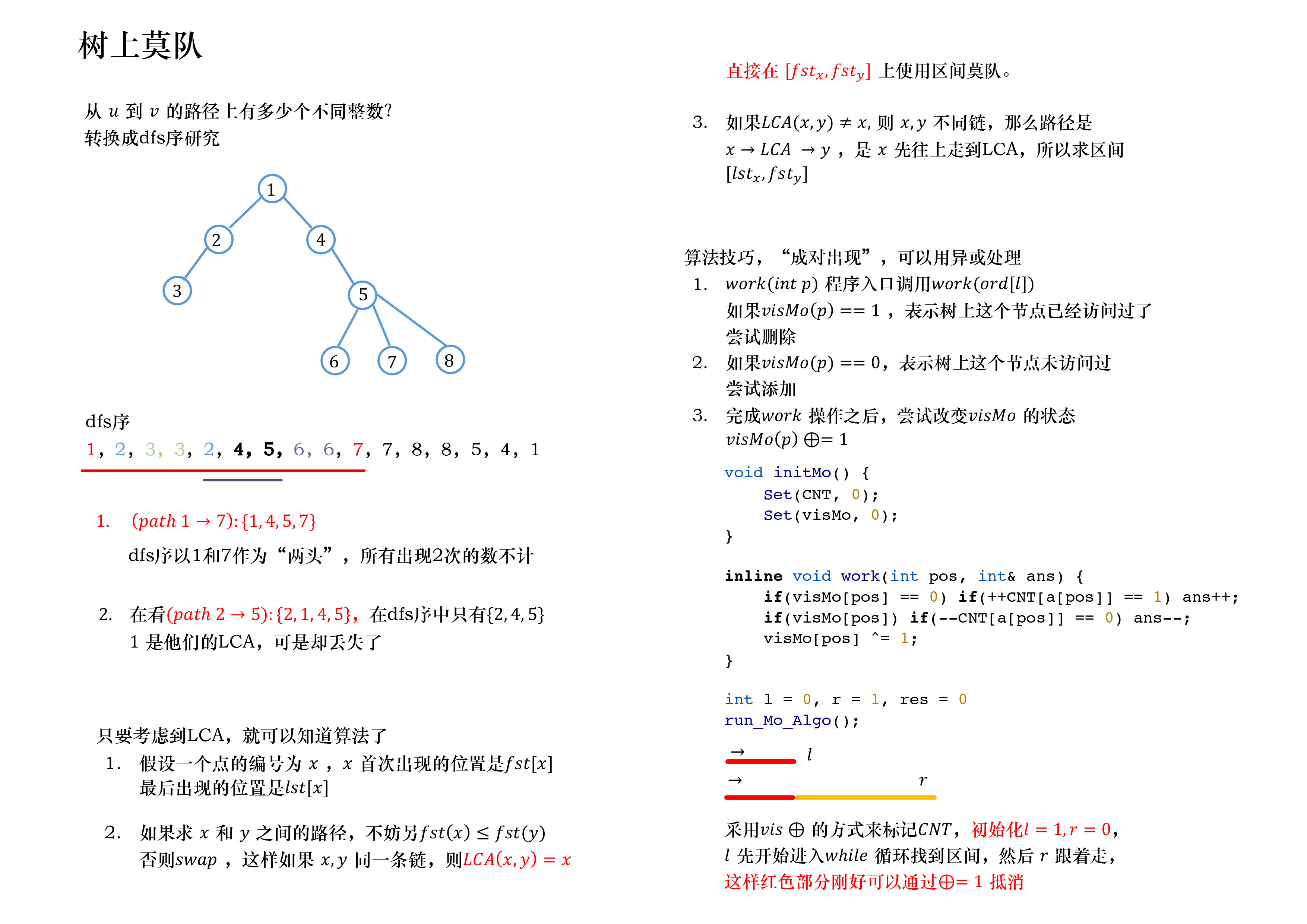
树上莫队初步
const int maxn = 200200;
int n, m, N;
int a[maxn], buf[maxn];
// == Graph structure ==
int head[maxn], nxt[maxn], ver[maxn];
int tot = 0;
void init() {
Set(head, 0);
Set(nxt, 0);
Set(ver, 0);
tot = 0;
}
void add(int x, int y) {
ver[++tot] = y; nxt[tot] = head[x]; head[x] = tot;
}
// == Graph structure finished ==
// == discrete ==
void discrete() {
sort(buf + 1, buf + 1 + n);
N = unique(buf + 1, buf + 1 + n) - buf - 1;
_rep(i, 1, n) a[i] = lower_bound(buf + 1, buf + 1 + N, a[i]) - buf;
}
// == dicrete finsihed ==
// == dfs order and lca ==
int f[maxn][30], dep[maxn];
int h = 0;
int fst[maxn], lst[maxn];
int ord[maxn], dfsn;
void initdfs() {
Set(dep, 0);
Set(fst, 0);
Set(lst, 0);
Set(ord, 0);
dfsn = 0;
dep[1] = 1;
h = 20 + 5;
}
void dfs(int x) {
assert(dep[1] == 1);
ord[++dfsn] = x;
fst[x] = dfsn;
for(int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if(dep[y]) continue;
dep[y] = dep[x] + 1;
f[y][0] = x;
_rep(k, 1, h) f[y][k] = f[f[y][k - 1]][k - 1];
dfs(y);
}
ord[++dfsn] = x;
lst[x] = dfsn;
}
int LCA(int x, int y) {
if(dep[x] > dep[y]) swap(x, y);
_forDown(i, h, 0) if(dep[f[y][i]] >= dep[x]) y = f[y][i];
if(x == y) return x;
_forDown(i, h, 0) if(f[y][i] != f[x][i]) {
x = f[x][i], y = f[y][i];
}
return f[x][0];
}
// == dfs order and lca finshed ==
// == query and block ==
class Qry {
public:
int l, r, lca, id;
};
Qry qry[maxn];
int belong[maxn];
int sz, t;
bool cmp(const Qry& a, const Qry& b) {
if(belong[a.l] ^ belong[b.l]) return belong[a.l] < belong[b.l];
if(belong[a.l] & 1) return a.r < b.r;
return a.r > b.r;
}
// [1, dfsn]
void block() {
sz = sqrt(dfsn);
t = dfsn / sz;
_rep(i, 1, t) _rep(k, (i - 1) * sz + 1, i * sz) belong[k] = i;
if(t * sz < n) {
t++;
_rep(k, (t - 1) * sz + 1, n) belong[k] = t;
}
}
// == query and block finsihed ==
// == Mo algorithm ==
int CNT[maxn];
int visMo[maxn];
void initMo() {
Set(CNT, 0);
Set(visMo, 0);
}
inline void work(int pos, int& ans) {
if(visMo[pos] == 0) if(++CNT[a[pos]] == 1) ans++;
if(visMo[pos]) if(--CNT[a[pos]] == 0) ans--;
visMo[pos] ^= 1;
}
int ANS[maxn];
int l = 1, r = 0, res = 0;
void solve() {
sort(qry + 1, qry + 1 + m, cmp);
_rep(i, 1, m) {
int ql = qry[i].l, qr = qry[i].r, qlca = qry[i].lca;
// printf("%d %d\n", ql, qr);
while (l < ql) work(ord[l++], res);
while (l > ql) work(ord[--l], res);
while (r < qr) work(ord[++r], res);
while (r > qr) work(ord[r--], res);
if(qlca) work(qlca, res);
ANS[qry[i].id] = res;
if(qlca) work(qlca, res);
}
}
// == Mo;s algo finished ==
int main() {
freopen("input.txt", "r", stdin);
init();
// == input data ==
scanf("%d%d", &n, &m);
_rep(i, 1, n) {
scanf("%d", &a[i]);
buf[i] = a[i];
}
_for(i, 1, n) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
// == input finished ==
// == discrete ==
discrete();
// == discrete finished ==
// == get dfs order and lca ==
initdfs();
dfs(1);
// == dfs order finished
// == block query ==
// == block query finished ==
// == check the arr ord[]
block();
_rep(i, 1, m) {
int l, r;
scanf("%d%d", &l, &r);
int lca = LCA(l, r);
//debug(lca);
if(fst[l] > fst[r]) swap(l, r);
qry[i].id = i;
if(l == lca) {
qry[i].l = fst[l];
qry[i].r = fst[r];
}
else {
qry[i].l = lst[l];
qry[i].r = fst[r];
qry[i].lca = lca;
}
}
// == Mo algorithm ==
initMo();
solve();
_rep(i, 1, m) printf("%d\n", ANS[i]);
}
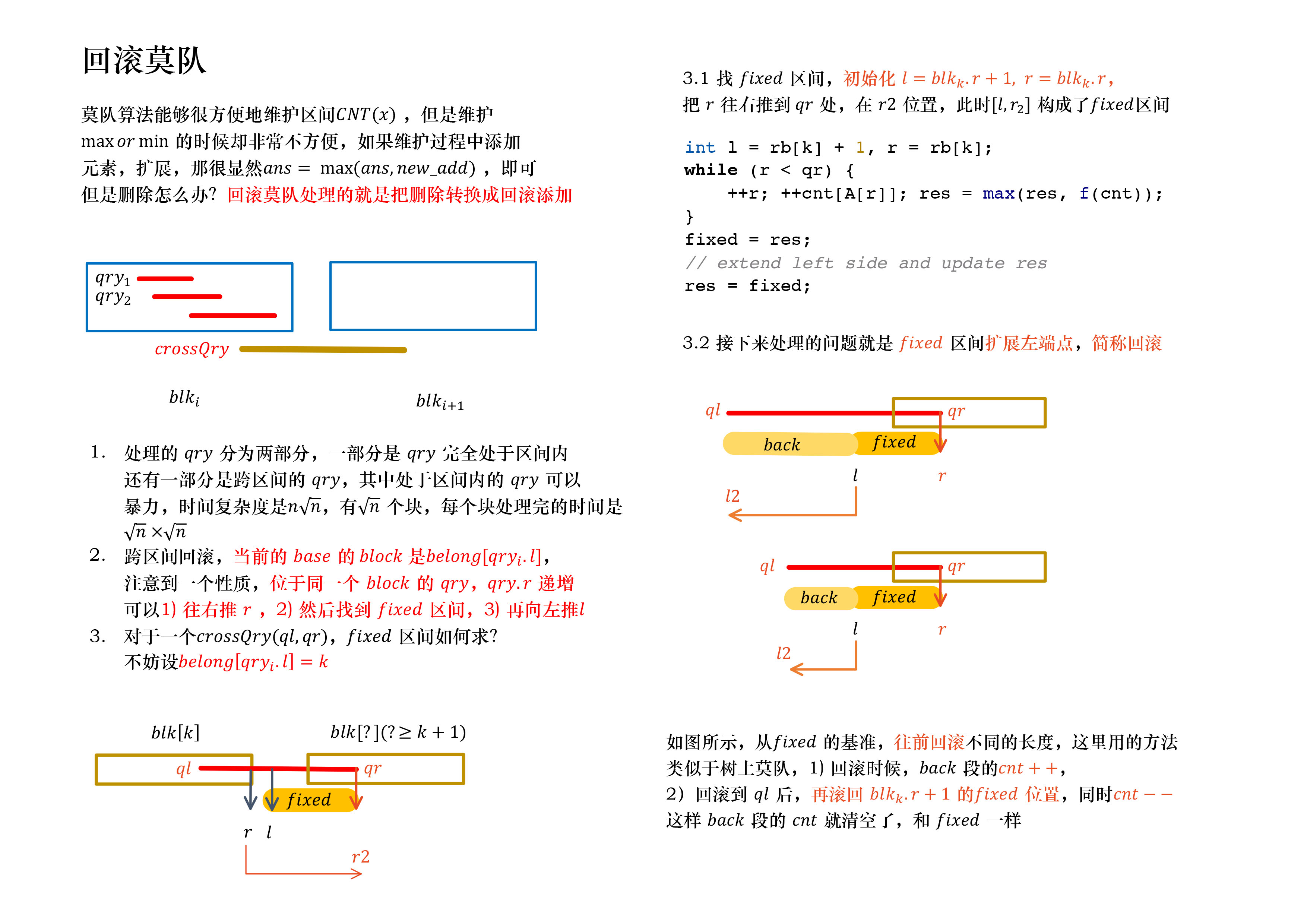
回滚莫队

const int maxn = 100000 + 10;
const int maxb = 5000;
int n, m, N;
int a[maxn], typ[maxn], inp[maxn];
class Qry {
public:
int l, r, id;
};
Qry qry[maxn];
// == discrete ==
void discrete() {
sort(inp + 1, inp + 1 + n);
N = unique(inp + 1, inp + 1 + n) - inp - 1;
_rep(i, 1, n) typ[i] = lower_bound(inp + 1, inp + 1 + N, a[i]) - inp;
}
// == discrete finished ==
// == block ==
int bl[maxn], br[maxn];
int belong[maxn];
int sz, t;
void block() {
sz = sqrt(n);
t = n / sz;
_rep(i, 1, t) {
bl[i] = (i - 1) * sz + 1;
br[i] = i * sz;
_rep(k, bl[i], br[i]) belong[k] = i;
}
if(t * sz < n) {
t++;
bl[t] = (t - 1) * sz + 1;
br[t] = n;
_rep(k, bl[t], br[t]) belong[k] = t;
}
}
bool cmp(const Qry& a, const Qry& b) {
if(belong[a.l] ^ belong[b.l]) return belong[a.l] < belong[b.l];
return a.r < b.r;
}
// == block finsihed ==
int cnt[maxn];
llong ANS[maxn];
void initMo() {
Set(ANS, 0);
Set(cnt, 0);
}
llong force(int ql, int qr) {
llong res = 0;
int tcnt[maxn];
_rep(i, ql, qr) tcnt[typ[i]] = 0;
_rep(i, ql, qr) {
tcnt[typ[i]]++;
res = max(res, (llong)1 * tcnt[typ[i]] * a[i]);
//debug(res);
}
return res;
}
void solve() {
sort(qry + 1, qry + 1 + m, cmp);
int i = 1;
_rep(k, 1, t) {
int l = br[k] + 1, r = br[k];
Set(cnt, 0);
llong res = 0;
// brute force for seg in block
for( ; belong[qry[i].l] == k; i++) {
int ql = qry[i].l, qr = qry[i].r;
if(belong[ql] == belong[qr]) {
llong ans = force(ql, qr);
ANS[qry[i].id] = ans;
continue;
}
llong fix = 0;
while (r < qr) {
r++;
++cnt[typ[r]];
res = max(res, (llong)1 * cnt[typ[r]] * a[r]);
//debug(res);
}
fix = res;
while (l > ql) {
l--;
++cnt[typ[l]];
res = max(res, (llong)1 * cnt[typ[l]] * a[l]);
//debug(res);
}
ANS[qry[i].id] = res;
//debug(res);
while (l < br[k] + 1) {
--cnt[typ[l]];
++l;
}
res = fix;
}
}
}
int main() {
freopen("input.txt", "r", stdin);
// == input ==
scanf("%d%d", &n, &m);
_rep(i, 1, n) {
scanf("%d", &a[i]);
inp[i] = a[i];
}
_rep(i, 1, m) {
int _l, _r;
scanf("%d%d", &_l, &_r);
qry[i].l = _l;
qry[i].r = _r;
qry[i].id = i;
}
// == input finished ==
// == discrete ==
discrete();
// == discrete finished ==
// == block ==
block();
// == block finished ==
// == Mo Algorithm ==
initMo();
solve();
// == Mo Algo finished ==
_rep(i, 1, m) printf("%lld\n", ANS[i]);
}
树状数组问题莫队式处理
莫队式处理,就是先根据询问的区间,对询问排序
然后再应用树状数组
const int maxn = 1000000 + 5;
class Fwick {
public:
vector<int> C;
int n;
void resize(int n) {
this->n = n;
C.resize(n + 1);
}
void clear() {
fill(C.begin(), C.end(), 0);
}
int sum(int x) {
int ret = 0;
while (x) {
ret += C[x];
x -= lowbit(x);
}
return ret;
}
void add(int x, int d) {
while (x <= n) {
C[x] += d;
x += lowbit(x);
}
}
int find(int l, int r, int val) {
while (l < r) {
int mid = (l + r) >> 1;
if(sum(mid) < val) l = mid + 1;
else r = mid;
}
return l;
}
};
Fwick fwick;
int A[maxn], N, vis[maxn];
int ANS[maxn];
int m;
void init() {
Set(vis, 0);
Set(ANS, 0);
}
class Qry {
public:
int l, r;
int id;
bool operator< (const Qry& rhs) const {
return r < rhs.r;
}
};
Qry qry[maxn];
void solve() {
_rep(i, 1, m) {
_rep(k, qry[i - 1].r + 1, qry[i].r) {
if(vis[A[k]]) fwick.add(vis[A[k]], -1);
vis[A[k]] = k;
fwick.add(vis[A[k]], 1);
}
ANS[qry[i].id] = fwick.sum(qry[i].r) - fwick.sum(qry[i].l - 1);
}
_rep(i, 1, m) printf("%d\n", ANS[i]);
}
int main() {
freopen("./input.txt", "r", stdin);
init();
scanf("%d", &N);
int maxv = 0;
_rep(i, 1, N) {
scanf("%d", &A[i]);
maxv = max(maxv, A[i]);
}
fwick.resize(maxn);
// == then input the query ==
scanf("%d", &m);
_rep(i, 1, m) {
scanf("%d%d", &qry[i].l, &qry[i].r);
qry[i].id = i;
}
sort(qry + 1, qry + 1 + m);
// == then solve the problem ==
solve();
}
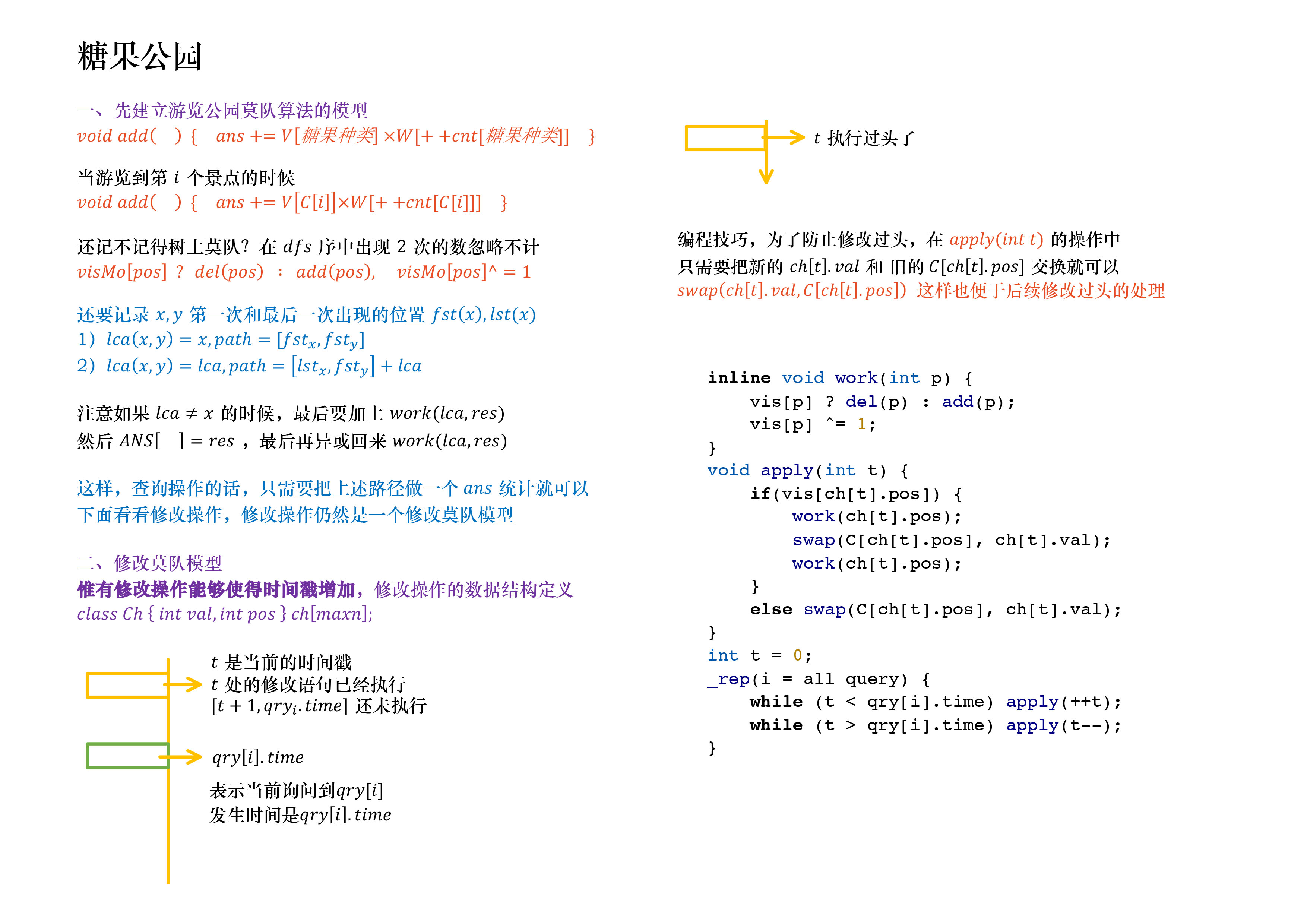
莫队算法综合
const int maxn = 200000 + 10;
// == Graph structure ==
int head[maxn], nxt[maxn], ver[maxn];
int tot = 0;
void initG() {
Set(head, 0);
Set(nxt, 0);
Set(ver, 0);
tot = 0;
}
void add(int x, int y) {
ver[++tot] = y;
nxt[tot] = head[x];
head[x] = tot;
}
// == Graph structure finished ==
// == get input ==
int V[maxn], W[maxn], C[maxn];
int cnt[maxn];
int n, m, q;
void init() {
Set(cnt, 0);
}
void getinp() {
scanf("%d%d%d", &n, &m, &q);
_rep(i, 1, m) scanf("%d", &V[i]);
_rep(i, 1, n) scanf("%d", &W[i]);
_for(i, 1, n) {
int u, v;
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
_rep(i, 1, n) scanf("%d", &C[i]);
}
// == input finished ==
// == get dfs order and lca ==
int fst[maxn], lst[maxn], dep[maxn], ord[maxn];
int f[maxn][30];
const int H = 25;
int dfn = 0;
void initdfs() {
Set(dep, 0);
Set(f, 0);
dep[1] = 1;
dfn = 0;
}
void dfs(int x) {
assert(dep[1] == 1);
ord[++dfn] = x;
fst[x] = dfn;
for(int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if(dep[y]) continue;
dep[y] = dep[x] + 1;
f[y][0] = x;
_rep(k, 1, H) f[y][k] = f[f[y][k - 1]][k - 1];
dfs(y);
}
ord[++dfn] = x;
lst[x] = dfn;
}
int getlca(int x, int y) {
if(dep[x] > dep[y]) swap(x, y);
_forDown(i, H, 0) if(dep[f[y][i]] >= dep[x]) y = f[y][i];
if(x == y) return x;
_forDown(i, H, 0) if(f[y][i] != f[x][i]) {
x = f[x][i], y = f[y][i];
}
return f[x][0];
}
// == dfs order and lca finished ==
// == get qry and change ==
class Qry {
public:
int l, r, id, time, lca;
};
Qry qry[maxn];
class Ch {
public:
int val, pos;
};
Ch ch[maxn];
int qn = 0, cn = 0;
void getinp2() {
_rep(i, 1, q) {
int op, x, y;
scanf("%d%d%d", &op, &x, &y);
if(op) {
int lca = getlca(x, y);
qry[++qn].time = cn;
qry[qn].id = qn;
if(fst[x] > fst[y]) swap(x, y);
if(x == lca) {
qry[qn].l = fst[x];
qry[qn].r = fst[y];
}
else {
qry[qn].l = lst[x];
qry[qn].r = fst[y];
qry[qn].lca = lca;
}
}
else {
ch[++cn].pos = x;
ch[cn].val = y;
}
}
}
// == qry and change finished ==
// == block ==
int belong[maxn];
int sz, t;
void block() {
sz = sqrt(dfn);
t = dfn / sz;
_rep(i, 1, t) _rep(k, (i - 1) * sz + 1, i * sz) belong[k] = i;
if(t * sz < dfn) {
t++;
_rep(k, (t - 1) * sz + 1, dfn) belong[k] = t;
}
}
int cmp(const Qry& a, const Qry& b) {
if(belong[a.l] ^ belong[b.l]) return belong[a.l] < belong[b.l];
if(belong[a.l] ^ belong[b.r]) return belong[a.r] < belong[b.r];
return a.time < b.time;
}
// == block finsihed ==
// == Mo algorithm ==
int visMo[maxn];
void push(int x, llong& ans) {
ans += (llong)1 * V[C[x]] * W[++cnt[C[x]]];
}
void del(int x, llong& ans) {
ans -= (llong)1 * V[C[x]] * W[cnt[C[x]]--];
}
void work(int x, llong& ans) {
visMo[x] ? del(x, ans) : push(x, ans);
visMo[x] ^= 1;
}
void apply(int t, llong& ans) {
if(visMo[ch[t].pos]) {
work(ch[t].pos, ans);
swap(ch[t].val, C[ch[t].pos]);
assert(visMo[ch[t].pos] == 0);
work(ch[t].pos, ans);
}
else swap(ch[t].val, C[ch[t].pos]);
}
llong ANS[maxn];
void solve() {
sort(qry + 1, qry + 1 + qn, cmp);
int l = 1, r = 0, ptime = 0;
llong ans = 0;
_rep(i, 1, qn) {
int ql = qry[i].l, qr = qry[i].r, qt = qry[i].time, qlca = qry[i].lca;
while (l < ql) work(ord[l++], ans);
while (l > ql) work(ord[--l], ans);
while (r < qr) work(ord[++r], ans);
while (r > qr) work(ord[r--], ans);
while (ptime < qt) apply(++ptime, ans);
while (ptime > qt) apply(ptime--, ans);
if(qlca) work(qlca, ans);
ANS[qry[i].id] = ans;
if(qlca) work(qlca, ans);
}
}
// == Mo algorithm finished ==
int main() {
freopen("input.txt", "r", stdin);
initG();
init();
getinp();
initdfs();
dfs(1);
getinp2();
block();
solve();
_rep(i, 1, qn) printf("%lld\n", ANS[i]);
}


oi-wiki
orz
大神
Orz
orz
太棒了