线性代数

行列式的概念

在二维空间中，给定两个 基向量，称以它们为 边 的正方形为 基准图形。

对这两个 基向量 进行 线性变化，得到以它们为边的 两边互相平行的 新图形。

而 新图形 和 基准图形 的 比值 就是 行列式的答案。

下面是用 容斥原理 解决二维行列式问题。

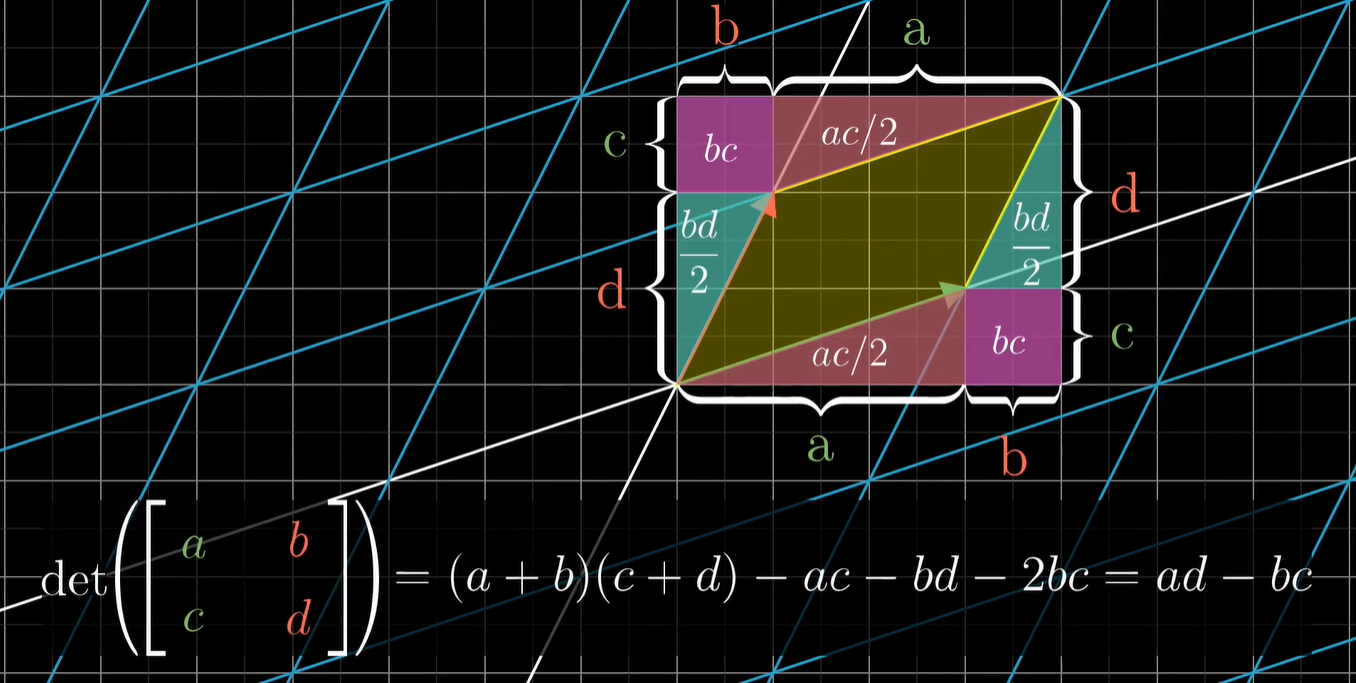
这样的 空间表示 同样可以扩展到 多维。

比如那三维行列式是这样的：

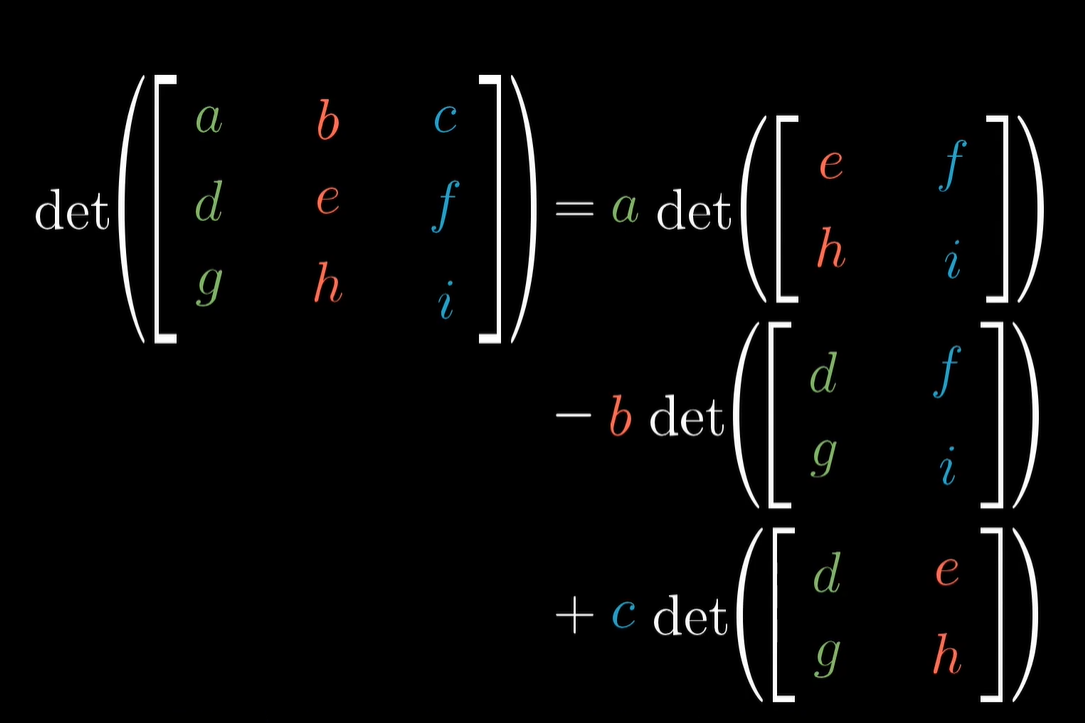
其中二维行列式部分可以理解为 面。

我们还能发现一个简单且有趣的性质：

对于矩阵的 两个线性变化 $M_1, M_2$，有 $det(M_1M_2) = det(M_1)det(M_2)$

原因是，$M_1,M_2$ 是缩放比例，满足 分配率。

扩展延伸

想一下，如果将线性变化拿来 解方程组 会怎么样呢？