二分详解

一、二分查找概述

二分查找，又称折半查找。
能够快速地从 顺序存储 的 有序 序列中查找元素。

顺序存储 ：算法要求快速地找到序列 中间元素 的下标，
像 链表 这类存储结构便不能满足。

有序：元素按一定顺序排列（比如 从大到小 或 从小到大 ）

二、二分查找原理简述

背景：对于元素 升序排序 的数组 arr ，
第一个元素下标为 0 ( L ) ，最后一个元素的下标为 R 。

询问：在数组中查找：是否存在数值 target ？
若存在请输出其 下标，若不存在则输出 -1 。

1. 找寻中间元素的下标 mid = ( L + R ) / 2

2. 判断中间元素是否是 if( arr[mid] == target )

3. 如果 arr[mid] == target 则输出 mid

4. 如果 arr[mid] != target 则可以 缩小判断的区间：( 已知数组 arr 升序排序 )

   ( 1 ) 如果 arr[mid] < target 则 L = mid + 1
   ( 2 ) 如果 arr[mid] > target 则 R = mid - 1

5. 由此重复执行上述过程，不断缩小区间直至找到元素 target ，
   或者区间 [ L , R ] 内没有元素，判断元素 target 不存在

第 4 步中区间的缩小是二分查找的 核心 。
每轮查找便能排除一半不可能的元素下标，极大地提高了查找效率。

{:height=”70%” width=”70%”}

即每次将答案所在的区间 缩小一半 ( 每次都 保证答案在区间中 )
当区间长度为 1 时，这个区间里的数就是结果。

该结果 一定存在，但它 不一定 是答案。

三、二分查找代码实现

// 设置全局变量 n 作为元素的个数
int binary_search( int arr[], int target )
{
    int L = 0, R = n - 1;
    while( L <= R ) // 说明 1
    {
        int mid = ( L + R ) / 2; // 说明 2

        // 调整区间 [ L , R ]
        if( arr[mid] > target )
            R = mid - 1; // [ L , mid - 1 ]
        else if( arr[mid] = target )
            return mid; // 找到 target
        else if( arr[mid] < target )
            L = mid + 1; // [ mid + 1 , R ]
    }
    return -1;
}

说明：

1 . 每轮循环的判断条件为 L <= R ，若换成 L < R 会怎么样？

( 1 ) 初始区间的设置 int L = 0, R = n - 1;，说明区间为数组两端真实的元素下标。
即判断 闭区间 [ L , R ]，
当执行到 L == R 时，区间内还有一个元素，仍要继续判断。
若换成 L < R，则会遗漏最后一个元素，因此 错误 。

// 上述错误在于最终 下标为 L == R 的点被遗漏
// 可以在此基础上改正，即补充判断最后的元素
... if( q[L] == x ) ...

( 2 ) 初始区间的设置 int L = 0, R = n; ，区间的右边不是真实的下标（越界），
即判断 开区间 [ L , R + 1 ），
当执行到 L == R 时，区间为 [ L , L ) 或 [ R , R )
此时循环判断条件改为 L < R 没有遗漏元素，正确 。

int binary_search( int arr[], int target ){
  int L = 0, R = n;
  while( L < R )
  ......
}

2 . mid 作为取两个数的中间值，会存在是否加 1 的问题，即

mid = ( L + R + 1 ) / 2
mid = ( L + R ) / 2

当 L + R 为偶数时，会存在中间取值的两种不同情况。

在上述二分查找算法中没有区别，但会在下面的算法中产生错误。

四、二分的本质

在二分搜索中，我们要求元素有序 ( 单调 )。
但 单调性 并 不是 二分的本质要求。

题目有单调性一定可以二分，可以二分的题目不一定非得有单调性

二分的本质是 边界，
其关键在于是否存在 某种性质 ，可以将数组 一分为二 。
左半边 的元素 满足 性质，而 右半边 元素 不满足，且两边没有交集。

而通过性质划分元素序列，就会在分界处产生左右两端的 边界 。
求解边界有关问题，才是二分的本质问题。

举例：在上述的二分查找中 ( 升序 ) ，性质为：以 target 为分界，
左边的元素 arr[x] < target ，右边的元素 arr[x] > target

二分要求元素有序，实际上是配合 target 将原序列一分为二，
从而达到将判断的个数减半的目的。

而这个 target 就可以看作一种特殊的边界。

五、应用场景 —— 整数二分

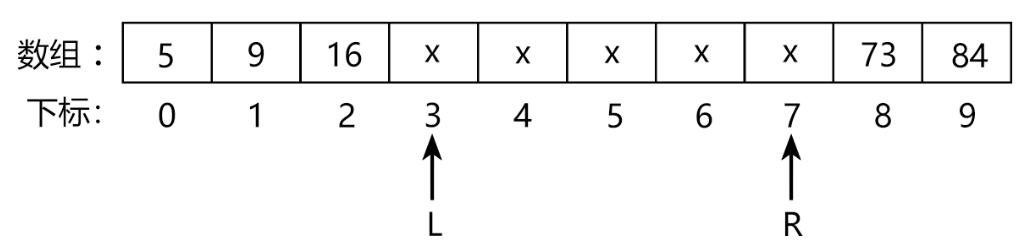
给定一个按照 升序 排列的长度为 n 的整数数组，
返回数组中一个元素 x 的 起始位置 和 终止位置 的下标。

( 数组中可能存在多个元素 x )

{:height=”70%” width=”70%”}

题源： 789. 数的范围 - AcWing题库

解题关键：当 q[mid] == target 时区间的调整。

六、二分代码实现

1. 计算左边界下标 ( 第一个 x 的下标 )

// 全局变量 n 为数组中元素的个数
int find_left( int q[], int target )
{
    int l = 0, r = n - 1; // 设置起始的区间 
    int mid;

    while( l < r )
    {
        mid = ( l + r ) / 2;
        if( q[mid] > target ) r = mid - 1;
        else if( q[mid] < target ) l = mid + 1;
        else if( q[mid] == target )
            r = mid; // 解题关键 
    }

    // 区间缩小到一个元素，其下标为 L ( L == R ) 
    // 若原数组中存在 target，则 q[L] == target，L 为其下标 
    if( q[l] == target ) return l; 
    else return -1; 
}

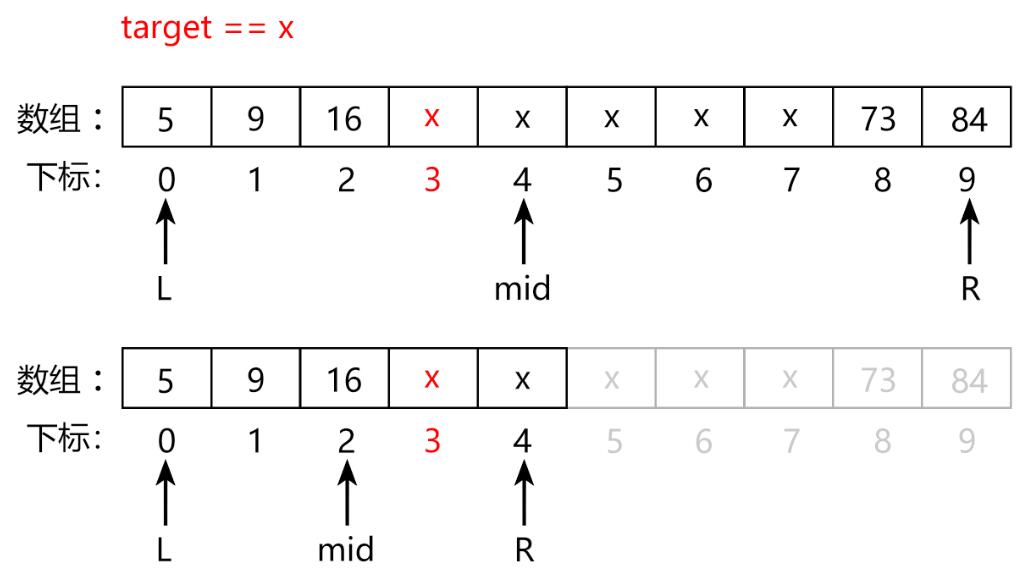
解题关键：

二分要求调整区间，得到的新区间 包含答案 。( 答案不能丢 )
当 q[mid] == target 时，答案有两种情况：

1. 当前元素 q[mid] 即为答案；
2. 答案还在 q[mid] 左边。

因此要向左缩小区间，r = mid 。
( 这里不能是 r = mid - 1 是因为 q[mid] 元素本身可能是答案 )

{:height=”70%” width=”70%”}

2. 计算右边界下标 ( 最后一个 x 的下标 )

// 与计算左边界函数 find_left 只有两处不同。
int find_right( int q[], int target )
{
    int l = 0, r = n - 1;
    int mid;

    while( l < r )
    {
        mid = ( l + r + 1 ) / 2; // 注意 mid 要加 1  
        if( q[mid] > target ) r = mid - 1;
        else if( q[mid] < target ) l = mid + 1;
        else if( q[mid] == target )
            l = mid; // 解题关键 
    }

    if( q[l] == target ) return l; 
    else return -1; 
} 

说明：

1. 区间的调整与左边界相同，当 q[mid] == target 时，
   要向右缩小区间，l = mid 。
2. 注意此处的 mid 在计算时需要 加 1 。

这是在递归或者循环中常见的易错点，若不加 1 可能会导致死循环。

区间的缩小有三种情形

​ ( 1 ) [ L , R ] ——> [ L , mid - 1 ] ( 对应 q[mid] > target )

​ ( 2 ) [ L , R ] ——> [ mid + 1 , R ] ( 对应 q[mid] < target )

​ 前两种情形不会出现死循环。

​ ( 3 ) [ L , R ] ——> [ mid , R ] ( 对应 q[mid] == target )

​ 当 L 与 R 相邻时 ( L + 1 == R )
​ 若使用 mid = ( L + R ) / 2 == L
​ 这样会产生 [ L , R ] ——> [ L , R ] ，导致死循环。

​ 同样，之前的 计算左边界 的模板，则不能使用 mid = ( L + R ) / 2 + 1

3 . 一般的题目中 mid 的计算需要考虑 防止溢出 问题

mid = left + ((right - left) >> 1)
mid = left + ((right - left) >> 1) + 1

补充说明：

本模板使用的循环判断条件为 while( L < R ) ，
因此区间最后剩下的元素不会在循环中判断，
而这个元素的下标即为 L ，用于之后的判断。

七、区间调整的简化

// 计算左边界下标
if( q[mid] > target ) r = mid - 1; // 调整边界 r
else if( q[mid] < target ) l = mid + 1;
else if( q[mid] == target )
    r = mid; // 调整边界 r

// 可简化为：
if( q[mid] >= target ) r = mid;
else l = mid + 1;

简化步骤说明：

1 . 合并了两个判断条件；

条件 q[mid] == target 可以合并到 调整相同的边界 的条件中。

2 . 用 else if 写全每一个判断条件能提高代码的可读性。
若足够熟练，则可以省略。

// 计算右边界下标
if( q[mid] > target ) r = mid - 1;
else if( q[mid] < target ) l = mid + 1; // 调整边界 l
else if( q[mid] == target )
    l = mid; // 调整边界 l

// 可简化为：
if( q[mid] <= target ) l = mid;
else r = mid - 1;

八、函数模板

#include <iostream>
using namespace std;

const int N = 100010;

int n, m;
int q[N];

int main()
{
    scanf( "%d%d", &n, &m );
    for( int i = 0; i < n; i++ ) scanf("%d", &q[i] ); 

    while( m-- )
    {
        int x;
        scanf( "%d", &x );

        int l = 0, r = n - 1;
        while( l < r ) // 计算左边界 
        {
            int mid = l + r >> 1;
            if( q[mid] >= x ) r = mid;
            else l = mid + 1;   
        } 

        if( q[l] != x ) printf( "-1 -1 \n" ); // 数组中没有元素 x 
        else // 只有存在元素 x，才能考虑左右边界 
        {
            printf( "%d ", l ); // 循环结束后，l 和 r 相等，均为左边界的下标 

            int l = 0, r = n - 1;
            while( l < r ) // 计算右边界
            {
                int mid = l + r + 1 >> 1;
                if( q[mid] <= x ) l = mid;
                else r = mid - 1;
            } 

            printf( "%d\n", l );
        }
    }
    return 0; 
}

九、应用场景 —— 浮点数二分

给定元素值 x，计算其 平方根 、 三次方根 。

题源： 790. 数的三次方根 - AcWing题库

十、浮点数二分

1. 开方运算与二分的关系

前面说过二分的本质在于某种 性质 划分的 边界 ，
开方运算之所以可以用二分来解，
可以理解为在数轴某个 区间 内找到一个数 mid ，这个数的乘方等于 x 。
在 mid 左边 的数的乘方均小于 x ，在 mid 右边 的数的乘方均大于 x 。

这个 mid 即为所求的边界。

2. 浮点数二分解题思路

​ ( 1 ) 对于给出的被开方数 x ，首先要确定其开方的结果所在的 区间 。
​ ( 2 ) 使用二分逐渐 缩小区间，直到找到答案。

由于开方之后的 结果 大多数情况下 不是整数，( 无限不循环小数 )
再加上计算机对于浮点数存在误差，因此无法求出一个确定的值。

处理方式：当区间缩小到 足够小 时，就将这个区间的 任意 左右边界作为答案。

十一、计算平方根 $\sqrt x $ 代码实现

#include<iostream>
using namespace std;

int main()
{
    double x;
    cin >> x;

    double l = -10000, r = 10000; // 结果所在区间初始设为 [ -10000 , 10000 ]
    while( ( r - l ) > 1e-8 ) // 当区间小于 10^(-8) ，则认为找到答案
    {
        double mid = ( l + r ) / 2;
        if( mid * mid >= x ) r = mid;
        else l = mid;
    }
    printf( "%f", l );
    // printf( "%f", r ); // 也可以
    return 0；
}

说明：

​ 1. 结果所在区间初始值的选取

​ $\sqrt x$ 的结果所在区间有两种情况：

​ ( 1 ) 当 x >= 1 时，$\sqrt x$ ∈ [ 0 , x ] ;
​ ( 2 ) 当 x <1 时，$\sqrt x$ ∈ [ 0 , 1 ] ，而不是 [ 0 , x ] 。

例如：$\sqrt {0.01} \;\; = \;\;0.1\;\; \notin \;\;[\;0\;,\;0.01\;]$

​ 模板中的处理方式：直接将初始区间设置为 [ -10000 , 10000 ] ，
​ 因为二分的特性 ( 折半 )，区间能很快缩小。

​ 2. 如何确定区间足够小

在上述模板中，当区间 [ L , R ] < 10^(-8) 则返回结果。

经验：若题目要求保留 m 位小数，则区间控制为 10^ - ( m + 2 )

例如：结果保留 4 位小数 ——> while( ( r - l ) > 1e-6 )
结果保留 6 位小数 ——> while( ( r - l ) > 1e-8 )
结果保留 8 位小数 ——> while( ( r - l ) > 1e-10 )

​ 3. 边界问题

在整数二分中，mid 的取值与区间的调整方式有关，
若取值不当，就有可能发生 死循环，其根本原因在于整数除法的 向下取整 机制。

但在浮点数二分中，就不会存在这种状况，
即 不会 有 ( L + R ) / 2 == L ，或 ( L + R + 1 ) / 2 == R
因此不存在这类边界问题。

十二、计算三次方根 $\sqrt[3]{x}$ 代码实现

#include<iostream>
using namespace std;

int main()
{
    double x;
    cin >> x;
    double l = -10000, r = 10000;

    // while( ( r - l ) > 1e-8 ) // 不使用这种方法

    for( int i = 0; i < 100; i++ ) // 直接循环 100 次
    {
        double mid = ( r + l ) / 2;
        if( mid * mid * mid >= x ) r = mid; // 三次方
        else l = mid;
    }
    printf( "%f", l );
    return 0;
}

说明：这里循环的条件不是当区间 [ L , R ] 足够小，
而是直接迭代 100 次，这样也能计算出一个近似精度的值。

十三、参考资料

1. y 总的课~~hh

2. 详解二分查找算法 - murphy_gb - 博客园 (cnblogs.com)

3. 算法面试题——二分查找套路法 - 知乎 (zhihu.com)

4. 二分查找又叫折半查找，是一种简单又快速的查找算法 (baidu.com)

（接受批评指正，欢迎交流补充~~ XD）