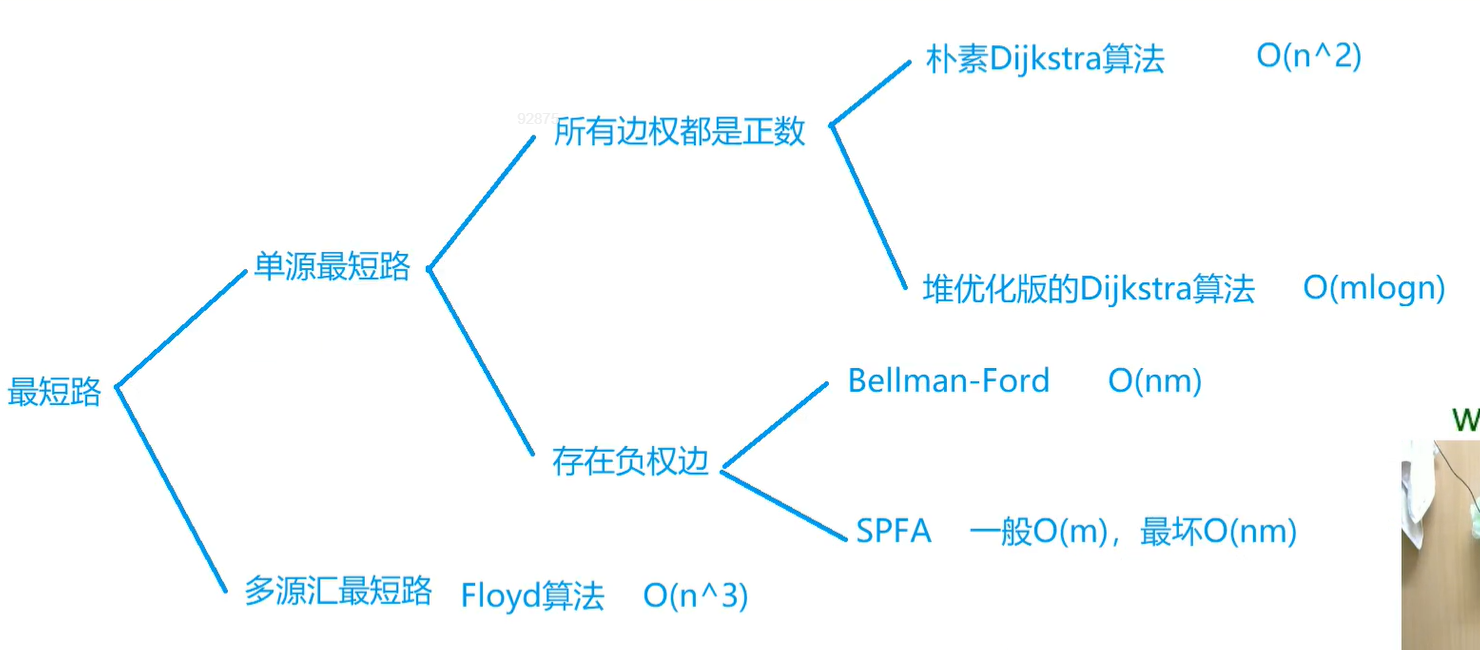
在算法基础课中所讲到的五种最短路径如下：
1.朴素dijkstra算法
2.堆优化的dijkstra算法
3.bellman_fold算法
4.spfa算法
5.floyd算法。
这五种算法使用于不同的情况，如下图：

朴素版本的dijkstra算法

朴素版本的dijkstra算法是基于贪心的思想，每次我们从所有未确定最短路径的点集V中挑出一个距离源点距离最短的点t，并加入到点集S(已经确定最短路径的点的集合)，并根据点t来更新集合V中其他点的最短路径，更新方式为dist[j]=min(dist[j],dist[t]+g[t][j])。

它适用于稠密图，存储方式为邻接矩阵。

设一个图中的顶点个数是n，边数是m，那么稠密图指的就是m>>n,m近似为n*n。

算法步骤

首先进行预处理，将令dist[1]=0;memset(dist,0x3f,sizeof dist);
1.从所有未确定最短路径的点集V中挑出一个距离源点距离最短的点t
2.将点t加入到点集s中，即st[t]=true;
3.根据点t来更新集合V中的其他点的最短路径

算法数据存储

计组里我学到的最重要的一点就是结构决定功能，要想实现什么样的功能，就有什么样的结构。这个道理放在算法里同样使用。由上面的步骤可以看出我们
1. 需要一个存放节点到达源点路径的数组dist；
2. 需要一个状态数组，判断当前节点是否已经加入最短路(或者说已经被访问过)；
3. 需要将每一个节点的连接关系存储起来，要么是邻接表，要么是邻接矩阵，由于边数远远大于点数，所以用邻接矩阵来存储。

C++代码

#include<iostream>
#include<cstring>
using namespace std;

//稠密图，边数是点数的平方
const int N=510;
int g[N][N],dist[N],ss[N];
int n,m;

void dijkstra(){
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;

    for(int i=0;i<n;++i){
        int t=-1;
        for(int j=1;j<=n;++j){
            if(!ss[j] && (t==-1||dist[t]>dist[j])){
                t=j;
            }
        }

        ss[t]=1;

        for(int j=1;j<=n;++j){
            if(!ss[j] && dist[j]>dist[t]+g[t][j]){
                dist[j]=dist[t]+g[t][j];
            }
        }
    }
}

int main(){
    memset(g,0x3f,sizeof g);
    scanf("%d %d",&n,&m);
    for(int i=0;i<m;++i){
        int x,y,weight;
        scanf("%d %d %d",&x,&y,&weight);
        g[x][y]=min(g[x][y],weight);
    }

    dijkstra();

    if(dist[n]==0x3f3f3f3f){
        cout<<-1;
    }else{
        cout<<dist[n];
    }
}

堆优化dijkstra算法

这个版本的dijkstra算法是由朴素版本的dijkstra算法优化而来。
它适用于稀疏图，存储方式为邻接表。
稀疏图与稠密图是一对相对的概念。

优化过程如下：
首先进行预处理，将令dist[1]=0;memset(dist,0x3f,sizeof dist);
(对于堆优化版本，预处理不变)
1.从所有未确定最短路径的点集V中挑出一个距离源点距离最短的点t
(对于朴素的dijkstra算法，它的时间复杂度是O(n),而对于堆优化版本，由于我们使用的是小根堆，所以时间复杂度是O(1))
2.将点t加入到点集s中，即ss[t]=1;
(对于堆优化版本，处理方式不变)
3.根据点t来更新集合V中的其他点的最短路径
(对于堆优化版本，将一个数加入到一个小根堆中，它的时间复杂度是O(log(n)))

堆优化的原因

我们之所以进行堆优化，是因为对于稀疏图来说，点数近似等于边数。朴素版的dijkstra算法的时间复杂度与点数的平方成正比，应用到稀疏图，时间复杂度就会太大。所以我们要想办法加快查找的速率，从而利用堆进行优化。

C++ 代码

#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;

const int N=150010;
int h[N],e[N],ne[N],w[N],idx;
int dist[N],ss[N];
int n,m;

void add(int x,int y,int weight){
    e[idx]=y;
    w[idx]=weight;
    ne[idx]=h[x];
    h[x]=idx++;
}

void dijkstra(){
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q;
    q.push({0,1});

    while(q.size()){
        auto a=q.top();
        q.pop();

        int ver=a.second,distance=a.first;
        if(ss[ver]) continue;
        ss[ver]=1;

        int i=h[ver];
        while(i!=-1){
            int j=e[i];
            if(!ss[j] &&dist[j]>dist[ver]+w[i]){
                dist[j]=dist[ver]+w[i];
                q.push({dist[j],j});
            }
            i=ne[i];
        }
    }
}

int main(){
    memset(h,-1,sizeof h);
    scanf("%d %d",&n,&m);
    while(m--){
        int x,y,weight;
        scanf("%d %d %d",&x,&y,&weight);
        add(x,y,weight);
    }

    dijkstra();

    if(dist[n]==0x3f3f3f3f){
        cout<<-1;
    }else{
        cout<<dist[n];
    }
}

bellman_fold算法

这个算法的核心操作就是双重循环，第一重循环n-1次，第二重循环m次，每次都对边进行松弛操作，其中，n是节点个数，m是边数。
存储方式：任意方式。可以是邻接表，也可以是邻接矩阵，也可以是结构体数组
预处理：dist[1]=0;memset(dist,0x3f,sizeof dist);

问题1 为什么第一重循环次数是n-1

假设一个图有n个顶点，那么从1号顶点走到n号顶点至多经过n-1条边。所以如果存在最短路径，那么经过n-1次的迭代，就一定可以得出结果的、

问题2 松驰操作是什么

设一条边的起点是a,终点是b,权重是w.dist[a]表示a到源点的距离，dist[b]表示b到源点的距离。松弛操作指的就是dist[b]=min(dist[b],dist[a]+w)。

问题3 为什么它是正确的

经过预处理后，只有1号点的距离是0，其他全部是无穷大。所以经过一次外重循环迭代后，1号点周围的节点的最短路径被更新了；再经过一次外重循环迭代，1号点周围节点的周围节点也会跟新，而且每次更新的结果都是最短路径。如此更新n-1次，就得到了到达n号点的最短路径。

C++代码

#include<iostream>
#include<cstring>
using namespace std;

typedef struct{
    int a,b,w;
}Edge;

const int M=10010,N=510;
int dist[N],last[N];
int n,m,Q;
Edge edge[M];

void bellman_ford(){
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    for(int i=0;i<Q;++i){
        memcpy(last,dist,sizeof dist);
        for(int j=0;j<=m;++j){
            auto e=edge[j];
            dist[e.b]=min(dist[e.b],last[e.a]+e.w);
        }
    }
}

int main(){
    scanf("%d %d %d",&n,&m,&Q);
    for(int i=0;i<m;++i){
        int x,y,weight;
        scanf("%d %d %d",&x,&y,&weight);
        edge[i]={x,y,weight};
    }

    bellman_ford();

    if(dist[n]>=0x3f3f3f3f/2){
        puts("impossible");
    }else{
        cout<<dist[n];
    }
}

spfa算法

spfa算法是对bellman_fold算法的优化。
beellman_fold算法是对所有所有的边都尝试松弛操作，但我们发现，并不是所有的边都实际进行了松弛操作。为了提高效率，我们把能进行松弛操作的节点放在一个集合当中，一直循环直到该集合为空。这个就是优化的过程。

我们采用什么数据结构或者方式来维护这样一个集合

借鉴BFS的思想，我们采用队列来维护这样一个集合，那么循环条件就是队列不空。

我们如何判断当前节点能否进行松弛操作

设一条边的起点是a,终点是b,权重是w.dist[a]表示a到源点的距离，dist[b]表示b到源点的距离。如果说dist[b]<=dist[a]+w,那么我们就认为b节点不能够进行松弛操作。由于b节点不能进行松弛操作，即dist[b]不变，那么与b节点相连通的节点也不会因为b节点而进行松弛操作。所以我们就不会把b节点加入到队列当中。例如，与b节点相邻的节点有c节点，d节点，由于b节点没有进行松弛操作，dist[b]没有改变，所以dist[b]+w(b,c)以及dist[b]+w(b,d)也不会改变，dist[c]与dist[b]+w(b,c)的大小关系也不会改变，c节点不会因为b节点而进行松弛操作。

一个小细节

在判断节点能否进行操作的过程中，可以会有一个节点距离源点的距离多次改变，那么说明这个节点多次符合要求。为了提升效率，我们定义了一个状态数组，它表示当前节点是否在队列中。如果已经在队列中，我们就不需要重复入队了，只需改变它的距离即可。当节点出队时，状态数组变为false，入队时，改为true。

C++代码

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;

const int N=100010;
int h[N],e[N],ne[N],w[N],idx;
int dist[N],ss[N];
int n,m;

void add(int x,int y,int weight){
    e[idx]=y;
    w[idx]=weight;
    ne[idx]=h[x];
    h[x]=idx++;
}
void SPFA(){
    memset(dist,0x3f,sizeof dist);
    queue<int> q;
    dist[1]=0;
    q.push(1);
    ss[1]=1;
    while(q.size()){
        int a=q.front();
        q.pop();

        ss[a]=0;//防止重复的节点被加入到队列中

        int i=h[a];
        while(i!=-1){
            int j=e[i];
            if(dist[j]>dist[a]+w[i]){
                dist[j]=dist[a]+w[i];
                if(!ss[j]){
                    q.push(j);
                    ss[j]=true;
                }

            }
            i=ne[i];
        }
    }

}
int main(){
    memset(h,-1,sizeof h);
    scanf("%d %d",&n,&m);
    for(int i=0;i<m;++i){
        int x,y,w;
        scanf("%d %d %d",&x,&y,&w);
        add(x,y,w);
    }
    SPFA();
    if(dist[n]>0x3f3f3f3f /2){
        puts("impossible");
    }else{
        cout<<dist[n];
    }
    return 0;
}

Floyd算法

该算法是基于动态规划的思想。它用来求解多源汇问题，也就是说，每一个节点都有可能是源点和汇点。
已知节点i和节点j，我们从节点i和节点j的最短路径所经过的节点来考虑问题。通过遍历1，2，3,……,n个节点，我们可以得到节点i和节点j经过<=1个节点的最短路径。如果最短路径经过n个点，那么我们就需要对i和j也进行遍历。
状态数组如下：
dist[k][i][j]=min(dist[k-1][i][j],dist[k-1][i][k]+dist[k-1][k][j]);k表示只经过前k个点，k-1表示只经过前K-1个点。

C++代码

#include<iostream>
#include<cstring>
using namespace std;

const int N=210;
int g[N][N];
int n,m,Q;

void floyd(){
    for(int i=1;i<=n;++i){
        g[i][i]=0;
    }

    for(int k=1;k<=n;++k){
        for(int i=1;i<=n;++i){
            for(int j=1;j<=n;++j){
                g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
            }
        }
    }
}

int main(){
    memset(g,0x3f,sizeof g);
    scanf("%d %d %d",&n,&m,&Q);
    while(m--){
        int x,y,w;
        scanf("%d %d %d",&x,&y,&w);
        g[x][y]=min(g[x][y],w);
    }

    floyd();

    while(Q--){
        int x,y;
        scanf("%d %d",&x,&y);
        if(g[x][y]>0x3f3f3f3f/2){
            puts("impossible");
        }else{
            cout<<g[x][y]<<endl;
        }
    }

}