线性DP & 区间DP & 计数类DP

动态规划相对于暴搜的优化：用一个数表示了一个集合中所有方案的属性，减少了搜索量

线性DP

递推公式具有线性的特点，比如沿着某一维线性的递推

AcWing 898. 数字三角形

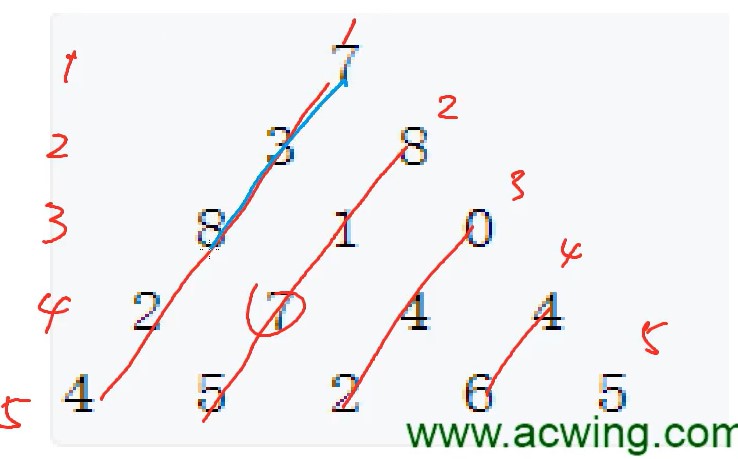
• 动态规划
  • 状态表示 f[i,j]
    • 集合:所有从起点出发，走到 (i,j) 的路径
    • 属性：集合当中所有路径上的数总和的最大值 $Max$
  • 状态计算
    • 划分:从左上方到 (i,j) 和从右上方到 (i,j)
    • 方程:f[i,j] = max(f[i-1,j-1]+a[i,j],f[i-1,j]+a[i,j])

时间复杂度：$O(状态数量\times 转移计算量)=O(n^{2})$

代码

突然发现倒序写法好快，不涉及到越界的问题，也不需要遍历找答案

AcWing 895. 最长上升子序列

• 动态规划
  • 状态表示 f[i]
    • 维数原则：一定要能把答案表示出来且能推出来，在此基础上维数越小越好
    • 集合：所有以第 $i$ 个数结尾的上升子序列
    • 属性：集合里每一个上升子序列的长度的最大值
  • 状态计算
    • 划分：以子序列倒数第二个数是否存在，若存在，则是数列中第几个数来划分
    • 方程：当 a[j] < a[i] 时，f[i] = max(f[j] + 1),0<=j<=i-1,j == 0表示序列无倒数第二个数
  • 输出子序列：加一个数组 g[N] ,记录每个状态是由哪个状态转移过来的，最后在沿着转移的轨迹输出序列
    • g[i] = j 表示状态 $i$ 是由状态 $j$ 转移过来的

时间复杂度

• 朴素法：$O(n^{2})$
  • 一维 $n$ ,每个状态的计算量级别为 $n$
  • 朴素法，最后要把状态 f[n] 全部再遍历一遍，找到最大值即为答案

朴素版代码

AcWing 896. 最长上升子序列 II

• 优化：去除冗余
  • 状态计算，从构建上升子序列的角度来看，每一个子序列都是在更小的子序列后加上一个符合要求的数得来的
  • 因此我们可以从头开始，先讨论只有一个数的最小子序列
    • 对于 $a_{i},a_{j},a_{i}\geq a_{j}$ ,在 $a_{i}$ 后接续的子序列（该序列第一个数在 $a_{j}$ 之后），一定也可以接续在 $a_{j}$ 后，而在 $a_{j}$ 后接续的子序列却不一定能接续在 $a_{i}$ 后
    • 所以 $a_{j}$ 是优于 $a_{i}$ 的，因此 考虑在长度为 $1$ 的子序列后接续时，考虑 $a_{j}$ 便不用考虑 $a_{i}$
  • 按照上述的思想，我们在考虑 a[k] 时，可以把 a[k] 之前的数组成的不同长度的上升子序列的最小末尾值存下来。要得出 f[k] ,可以通过二分查找在数组中找到 a[k] 能接上的最长子序列，并更新其他子序列最小末尾值
  • 可以证明，存末尾值的数组中所有数一定是严格上升序列，否则一定有某长度的末尾值不是最小末尾值

时间复杂度

优化：$O(n\log n)$

优化版代码

AcWing 897. 最长公共子序列

• 动态规划
  • 状态表示 f[i,j]
    • 集合：所有在第一个序列的前 $i$ 个字母中出现且在第二个序列的前 $j$ 个字母中出现的公共子序列
    • 属性：集合里的所有子序列长度的最大值
  • 状态计算
    • 划分：以 a[i] b[j] 是否包含在子序列当中来划分，共四种情况
      • a[i] b[j] 都无：f[i-1,j-1]
      • a[i] b[j] 都有：f[i-1,j-1]+1
      • 一有一无，如果用 f[i-1,j] f[i,j-1] 来表示，很明显是不准确的，虽然可以完全包含，但会重复计算 f[i - 1][j - 1] 。动态规划划分集合的原则是不重不漏，可遇到实际问题时，原则不一定要严格遵守。由于本题求的是最大值，因此产生重复是完全不影响答案的，于是我们仍然可以用 f[i-1,j] f[i,j-1] 来表示 a[i] b[j] 一有一无的情况
        • 如果碰到集合属性是数量时，那就要严格保证不重复
      • 在重复的情况下，f[i-1,j-1] 会被重复考虑，因此在代码中可以不写这种情况
    • 方程：f[i,j]=max(f[i-1,j],f[i,j-1],f[i-1,j-1]+1)

代码

AcWing 902. 最短编辑距离

• 动态规划
  • 状态表示 f[i,j]
    • 集合：所有将 a[1~i] 变成 b[1~j] 的操作方式
    • 属性：集合中所有操作方式的次数最小值 $Min$
  • 状态计算
    • 划分：a[1~i] 变成 b[1~j] 的最后一步操作
      • 删：要求 a[1,i-1] 和 b[1,j] 匹配
        • 算式： f[i-1,j] + 1
      • 增： a[1,i-1] 通过操作能变成 b[1,j-1] ，最后加上 b[j]
        • 算式：f[i,j-1]+1
      • 改：先让 a[1~i-1] 匹配上 b[1~j-1],再判断，如果 a[i] != b[j] , 则要让 a[i] = b[j]
        • 算式：f[i-1,j-1] + 1 or 0
    • 方程：f[i,j]=min(f[i-1,j] + 1,f[i,j-1]+1,f[i-1,j-1] + 1 or 0)

时间复杂度：$O(3n^{2})=O(n^{2})$

代码

AcWing 899. 编辑距离

上一题的重复操作

代码

区间DP

区间DP常用循环方式：区间长度从小到大循环，内部左端点从小到大循环，再枚举状态

AcWing 282. 石子合并

• 动态规划
  • 状态表示
    • 集合：所有将第 $i$ 堆石子到第 $j$ 堆石子合并成一堆石子的合并方式
    • 属性：集合中所有合并方式的代价最小值 $Min$
  • 状态计算
    • 划分
      • 划出一条分界线，把区间分为左右两部分，先把左右两部分分别合并，再统一合并
      • 用这条分界线的位置来划分集合
    • 方程：f[i,j]=f[i,k]+f[k+1.j]+s[j]-s[i-1],k=0,1,2,...,j-2,j-1
      • 区间和用前缀和算法计算

时间复杂度：$O(n^{3})$

代码

计数类DP

AcWing 900. 整数划分

• 方法一：看成完全背包问题
  • 背包体积为 $n$ ,有体积为 $1,2,…,n$ 的 $n$ 种物品，求正好装满背包的挑选方案数
  • 动态规划
    • 状态表示 f[i,j]
      • 集合：从前 $i$ 个物品中选，体积恰好是 $j$ 的所有选法
      • 属性：集合中选法的数量
    • 状态计算
      • 划分：按第 $i$ 个物品的选择个数划分
      • 方程：f[i,j] = f[i-1,j]+f[i-1,j-i]+f[i-1,j-2*i]+...+f[i-1,s*i]
  • 优化：类似完全背包的优化
    • f[i,j] = f[i-1,j]+f[i-1,j-i]+f[i-1,j-2*i]+...+f[i-1,s*i]=f[i-1,j]+f[i,j-i]
    • 进一步优化成一维
• 方法二
  • 动态规划
    • 状态表示
      • 集合：所有总和是 $i$ ，且恰好表示成 $j$ 个数之和的方案
      • 属性：集合元素数量
    • 状态计算
      • 划分：按 $j$ 个数中的最小数划分
        • 最小数为 $1$：f[i-1,j-1]
        • 最小数大于 $1$：把每个数都减去 $1$ ,方案数不变 f[i-j,j]
      • 方程
        • f[i,j] = f[i-1,j-1] + f[i-j,j]
        • ans = f[n,1] + f[n,2] + ... + f[n,n] 这步是方法一不需要的，但方法二需要
        • 由于要用到一维的 $i-j$ ，所以不能把一维优化掉

时间复杂度

二维：$O(n^{2}\log n)$

优化后：$O(n^{2})$

代码