高精度算法详解

一、高精度算法简介

变量 无法 直接 存储 非常庞大 的数字 ( 高精度数 )，也就不能直接进行常规的数值计算。
高精度算法通过 模拟 的方式实现 高精度数 的 加 减 乘 除 等数值计算。

高精度数：小数点后几百位或者更多，或是几千亿几百亿的大数字。

二、高精度算法的常见考查方式

1. 两个大整数相加 A + B ( A 和 B 的位数 ( 长度 ) len( A ) 和 len( B ) 大概为 10^6 )；

2. 两个大整数相减 A - B ；

3. 一个大整数乘上一个小整数 A * a ( len( A ) ≤ 10^6，| a | ≤ 10^9 or | a | ≤ 10000 )；

4. 一个大整数除以一个小整数 A / a ( 求 商 和 余数 )。

说明：len( A ) 是指数值 A 的长度，例如：A = 123456，len(A) = 6

三、大整数数值的存储

单个变量的存储范围有限，不够存储大整数。
我们通过数组，分别存储大整数的各个位数。

1. 存储方式

数值低位存储在数组低位，例如

数值：123456789

数组 a[ 9 ] = { 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 }

2. 代码实现

string a; // 大的非负正整数，不能用 整型 变量存储 
cin >> a;

vector<int> A;  // 用于存放拆分的 大整数 

// 逆序存储
for( int i = a.size() - 1; i >= 0; i-- ) A.push_back( a[i] - '0' ); 

3. 逆序存储的原因

1. 在 手动实现加减 法时，我们习惯从 低位 ( 个位 ) 开始，( 从后往前 )
   在处理 数组 时，我们习惯从 第一个 元素开始。( 从前往后 )

2. 加法中会向高位 进位，减法中会向高位 借位。
   将数字逆序存储在数组中，对高位 ( 前一位 ) 数字的处理，
   只要处理数组的下一个元素 ( 下标 + 1 ) 。

3. 加法、乘法，其结果的 高位长度不确定，会向前增加
   例如加法中最高位再进位，
   但在数组的处理中，
   向末尾增加一个元素简单 O(1) ，向开头增加一个元素困难 O(n)

4. 综上，在 加减乘 三种运算中，使用逆序存储，处理更简单。
   在同一个程序中，可能会同时运用 加减乘除 四种运算，
   因此虽然除法习惯从高位开始计算，但为了能统一处理，也选择逆序存储。

四、高精度加法

1. 应用场景

给定两个大整数 A 、B ( 不含前导 0 )，计算 A + B 。

前导 0 ：即高位的没有意义的 0 。
例如：对于整数 000789 == 789，前者含有前导 0 。

题源： 791. 高精度加法 - AcWing题库

2. 解题思路

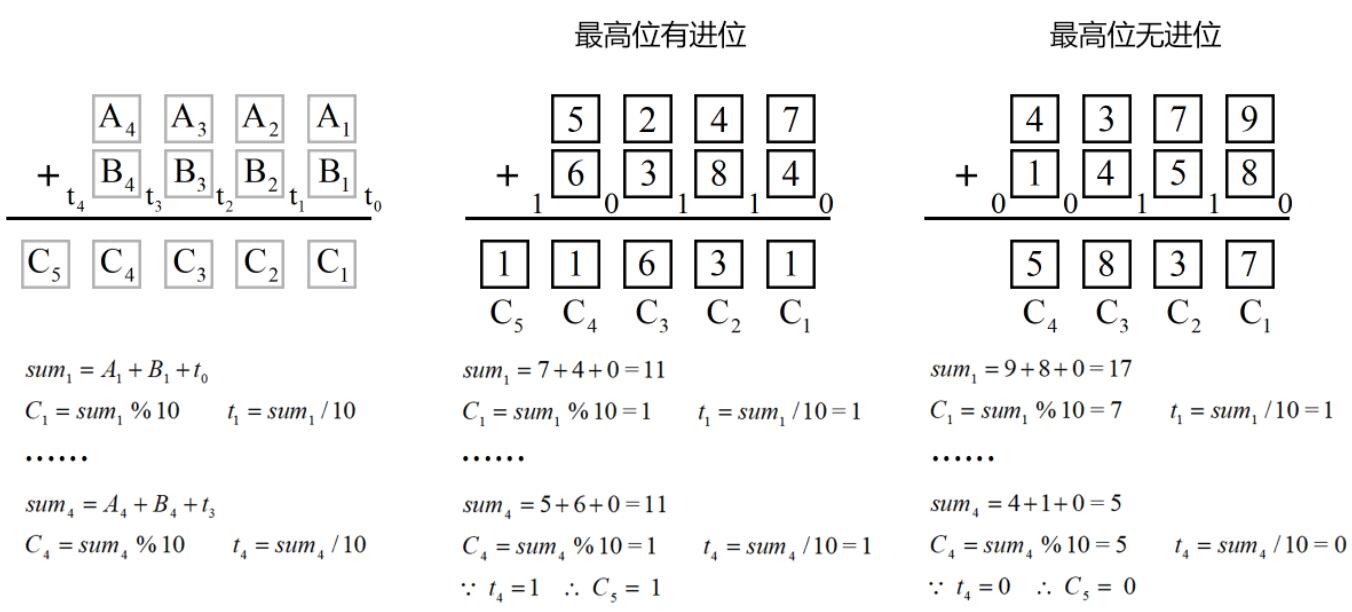
模拟加法的实现过程

1. 将两个数按个位对齐，从个位开始相加；

2. 各个 数位 上数值相加，再加上前一位 进位 t ，得到和 sum ；

3. 根据和，求出该数位的 结果 和 新的进位 。

3. 函数模板 —— 高精度加法

#include <iostream>
#include <vector>
// 使用 vector 向量的原因是它自带 长度 ( size ) 属性
// 使用一般的数组也行，但需要另外开辟一个变量记录长度 ( 即位数 ) 。

using namespace std;

// 参数中，不加引用 &，则调用函数时会把向量 vector 整体复制一份
// 增加引用则不会，能提高速度 
vector<int> add( vector<int> &A, vector<int> &B )
{
    vector<int> C; // 用于存放结果 

    int t = 0; // 用于存放 进位值 ，对于 个位，进位为 0 
    for( int i = 0; i < A.size() || i < B.size(); i++ )
    {
        // 各个位数 同进位 t 相加 
        if( i < A.size() )  t += A[i];
        if( i < B.size() )  t += B[i];
        C.push_back( t % 10 ); // 计算出每位结果
        t /= 10; // 计算下一位进位 
    }   
    if( t ) C.push_back(1); // 判断最高位是否有进位 

    // 使用 t 也行，因为在加法背景下，进位只有 0 / 1（即有 / 无进位）
    // if( t ) C.push_back( t ); 

    return C;   // 返回结果向量 
}

vector<int> add( vector<int> &A, vector<int> &B )
{
    vector<int> C;
    int t = 0;

    for( int i = 0; i < A.size() || i < B.size(); i++ )
    {
        if( i < A.size() )  t += A[i];
        if( i < B.size() )  t += B[i];

        C.push_back( t % 10 );
        t /= 10; 
    }   
    if( t ) C.push_back(1);

    return C;
}

注意事项：

1. 用 vector 逆序存储 大整数，注意从字符型到整数型数据的 类型转换 ；

2. 注意加法最后要判断最高位是否有进位；

五、高精度减法

1. 应用场景

给定两个大整数 A 、B ( 不含前导 0 )，计算 A - B 。

( A 和 B 都是正数，但 A 和 B 的大小关系不确定 )

题源： 792. 高精度减法 - AcWing题库

2. 解题思路

( 1 ) 首先要判断 A 、B 的大小关系

1. 若 A > B ，则直接计算，

2. 若 A < B ，则计算 B - A ，在其结果前面加负号 -

// 判断是否有 A >= B 
bool cmp( vector<int> &A, vector<int> &B )
{
    // 两数长度不同时，长度更长的数字 更大 
    if( A.size() != B.size() ) return A.size() > B.size(); 

    // 长度相同，从高位开始向低位比较
    // 但要注意向量中数据逆序存储，最后一位是最高位
    for( int i = A.size() - 1; i >= 0; i-- )
        if( A[i] != B[i] )  // 遇到第一个不同的数字 
            return A[i] > B[i];

    return true; // 两个数是相等的 A = B，满足 A >= B，返回 true
}

( 2 ) 模拟减法的实现过程

1. 将两个数按个位对齐，从个位开始相减；
2. A 的当前数位先减去低位的 借位 ，再减去 B 对应数位，得到数值 t；
3. 通过 t 的符号，判断是否需要借位；
4. 求出该数位的 结果 和 新的借位 。

3. 函数模板 —— 高精度减法

vector<int> sub( vector<int> &A, vector<int> &B )
{
    vector<int> C;  // 用于存放结果 

    // 调用 sub 函数前，已经通过 cmp 判断，保证 A >= B

    int t = 0; // t 表示借位，个位没有借位，初始值为 0 

    for(int i = 0; i < A.size(); i++ )  
    {
        t = A[i] - t; // 减去低位的借位

        if( i < B.size() )  t -= B[i]; // B < A，因此 B 的长度可能小于 A

        C.push_back( ( t + 10 ) % 10 ); // 计算当前数位的结果

        if( t < 0 ) t = 1;  // 若 t < 0, 说明已经借位了，此时 t 的值重新表示借位 1
        else t = 0;
    }

    while( C.size() > 1 && C.back() == 0 ) C.pop_back(); // 去掉前导 0

    return C;
}

vector<int> sub( vector<int> &A, vector<int> &B )
{
    vector<int> C;
    int t = 0;

    for(int i = 0; i < A.size(); i++ )  
    {
        t = A[i] - t;
        if( i < B.size() )  t -= B[i];

        C.push_back( ( t + 10 ) % 10 );

        if( t < 0 ) t = 1;
        else t = 0;
    }

    while( C.size() > 1 && C.back() == 0 ) C.pop_back();

    return C;
}

注意事项：

1. A 和 B 的大小关系不确定，要先进行判断；

2. 减法的结果可能会包含前导零，要除去，但当结果就是 1 个 0 时要保留。

说明：

每数位结果的计算：C.push_back( ( t + 10 ) % 10 );

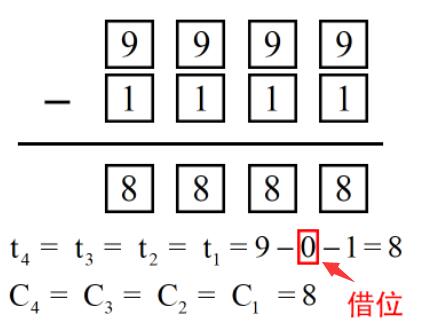
1. 当 t >= 0 ，( t + 10 ) % 10 == 0

对于当前数位 A[i] - B[i] >= 0 ，够减，不需要借位，t 即答案

{:height=”30%” width=”30%”}

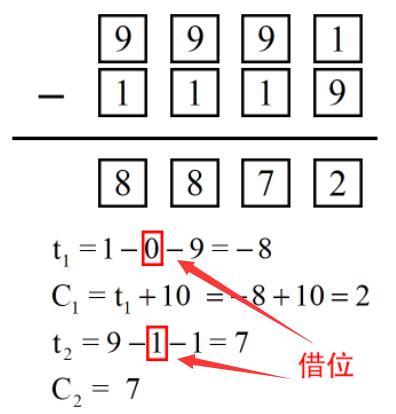
1. 当 t < 0 ，( t + 10 ) % 10 == t + 10

对于当前数位 A[i] - B[i] < 0 ，不够减，需要借位，为答案 t + 10

{:height=”30%” width=”30%”}

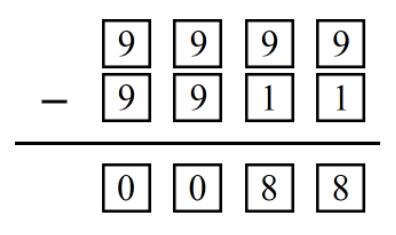
前导 0 的产生：

{:height=”30%” width=”30%”}

六、高精度乘法

1. 应用场景

给定两个非负整数 ( 不含前导 0 ) A 和 B，计算 A × B 的值。

( 其中 A 为大整数，B 为较小的正整数 )

题源：793. 高精度乘法 - AcWing题库

2. 解题思路

将 乘数 B 看成一个整体，与 被乘数 的 每位 相乘，
并将各个乘积按照 实际的权值，计算出结果中的各个 数位 。

举例：从权值的角度能更好地理解算法

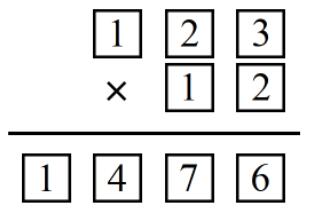{:height=”30%” width=”30%”}

$$ \begin{array}{l} 123*12\\\\ = \;\;3\*12 + \;20\*12 + \;100\*12\\\\ = (\;3\*12\;)\*1 + \;(\;2\*12\;)\*10 + \;(\;1\*12\;)\*100 \end{array} $$

1. 对于 被乘数 的 个位 ， t = 3 * 12 = 36 ，
   要确定 结果 个位 的值，即要确定 t 中有多少个 1 ：
   t = 36 中，有 6 个 1 ( 36 % 10 ) ，有 3 个 10 ( 36 / 10 ) （ 个位：6 ）
2. 对于 被乘数 的 十位 ， t = 2 * 12 = 24 ，有 24 个 10 ，再加上之前产生的 3 个 10 ，
   所以共有 27 个 10 ( t = 24 + 3 = 27)
   要确定 结果 十位 的值，即要确定 t 中有多少个 10 ：
   t = 27 中，有 7 个 10 ( 27 % 10 ) ，有 2 个 100 ( 27 / 10 ) （ 十位：7 ）
3. 对于 被乘数 的 百位 ， t = 1 * 12 = 12 ，有 12 个 100 ，再加上之前产生的 2 个 100 ，
   所以共有 14 个 100 ( t = 12 + 2 = 14)
   要确定 结果 百位 的值，即要确定 t 中有多少个 100 ：
   t = 14 中，有 4 个 100 ( 14 % 10 ) ，有 1 个 1000 ( 14 / 10 ) （ 百位：4 ）
4. 由于最终 t = 1 ，说明仍需要向高位进位。
   要确定 结果 千位 的值，即要确定 t 中有多少个 1000 。（ 千位：1）

3. 函数模板 —— 高精度乘法

vector<int> mul( vector<int> &A, int b)
{
    vector<int> C;  // 用于存储结果

    int t = 0;  // 保存 大整数 A 每位 与 乘数 的积 

    // 循环有两个条件
    // 1. 大整数 A 各数位均要进行计算
    // 2. 大整数各数位计算完，但 t 仍有剩余，则还需要向前进位 ( t != 0 ) 
    for( int i = 0; i < A.size() || t; i++ )
    {
        if( i < A.size() ) t = A[i] * b + t; // 大整数每位与乘数相乘，再加上进位 

        C.push_back( t % 10 ); // 求出当前数位的值 
        t /= 10; // 进位 
    }

    // 当乘数 b 为 0，则计算出的每位均为 0 ( 即产生前导 0 ) 
    while( C.size() > 1 && C.back() == 0 )  C.pop_back();

    return C;
}

vector<int> mul( vector<int> &A, int b)
{
    vector<int> C;
    int t = 0;

    for( int i = 0; i < A.size() || t; i++ )
    {
        if( i < A.size() ) t = A[i] * b + t;

        C.push_back( t % 10 );
        t /= 10;
    }

    while( C.size() > 1 && C.back() == 0 )  C.pop_back();

    return C;
}

注意事项：当乘数 b 为 0，则计算出的每位均为 0 ( 即产生前导 0 ) 。

七、高精度除法

1. 应用场景

背景：被除数 A 为非负大正整数，除数 b 为小整数

题源：794. 高精度除法 - AcWing题库

2. 解题思路

与 加减乘 不同，除法从 高位 开始算，
但是为了和上述模板统一，因此也选择 逆序存储。

实现过程与手动计算除法完全相同。

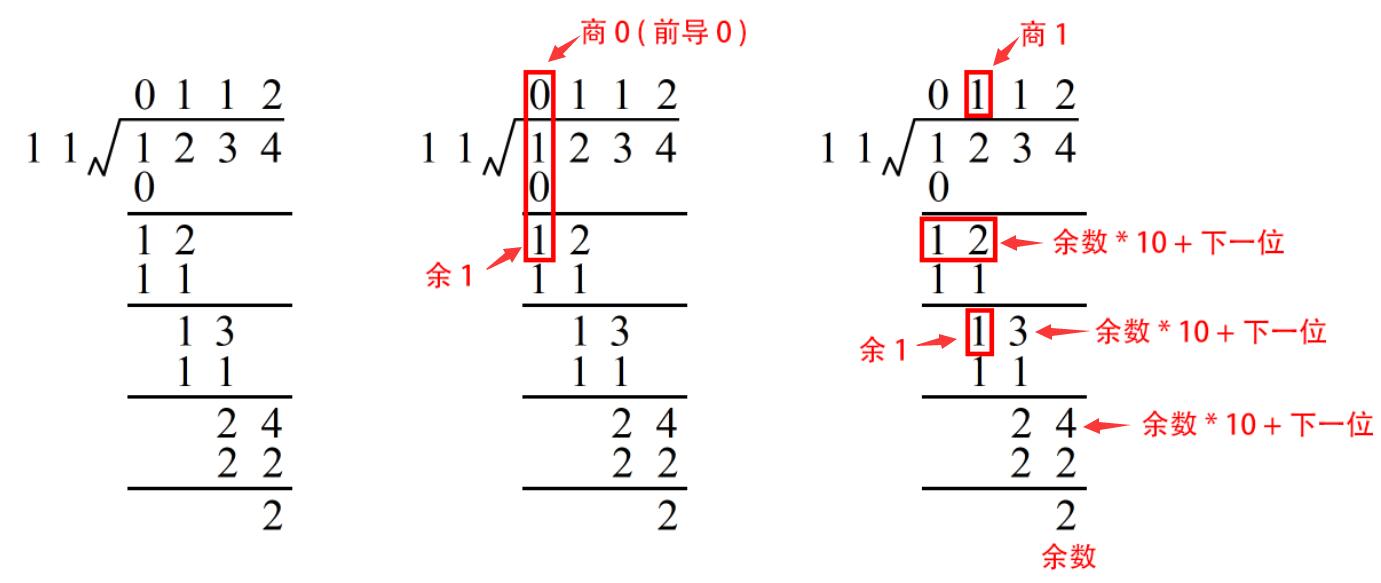
3. 函数模板 —— 高精度除法

// A / B ，商是 C ，余数是 r
vector<int> div( vector<int> &A, int b, int &r) // 余数 r 通过引用方式返回 
{
    vector<int> C; // 商 
    r = 0;
    for( int i = A.size() - 1; i >= 0 ; i-- ) // 除法从高位向低位运算 
    {
        r = r * 10 + A[i]; // 余数 * 10 + 下一位 
        C.push_back( r / b); // 商
        r %= b; // 余数 
    }
    // 上述计算中，结果顺序存储

    // reverse 函数需要包含头文件，#include<algorithm>
    reverse(C.begin() , C.end()); // 将向量中的元素颠倒顺序 ，形成结果的逆序 

    while( C.size() > 1 && C.back() == 0 ) C.pop_back(); // 删除前导 0 
    return C;
}

vector<int> div( vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for( int i = A.size() - 1; i >= 0 ; i-- )
    {
        r = r * 10 + A[i];
        C.push_back( r / b);
        r %= b;
    }

    reverse(C.begin() , C.end());

    while( C.size() > 1 && C.back() == 0 ) C.pop_back();
    return C;
}

注意事项:

1. 除法从 高位 开始计算；
2. 由于除法从高位开始计算，因此最初结果为 顺序 存储，
   要 按照需求 选择是否将其转换为 逆序 存储。
3. 注意消除 前导 0。

八、参考资料

1. y 总的课hh~~

2. 高精度算法_百度百科 (baidu.com)

（接受批评指正，欢迎交流补充~~ XD）