初见安~这里是第一次写Acwing：）欢迎到博客原址食用：YingLi的博客
全程图丑不要在意，最好都自己画一画

一、强连通分量（for有向图）

初次见到这个名词，想必一定感觉很高级。（因为不知道） 事实上也是很好理解的。

1.定义

强连通分量是针对的有向图而言——

首先，如果一个有向图中，对于任意两点x、y，均存在x到y和y到x的路径，则称这个图为强连通图。（流图）如果这个图就是一个环，就是一个典型的强连通图。

而对于一个普通的有向图而言，在如上定一下的最大强连通子图为其强联通分量。

我们来看个例子会好理解一些——

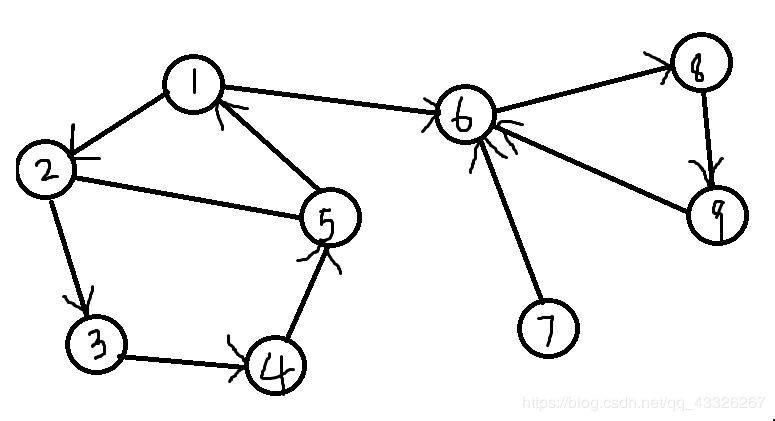
如图我们可以发现：5 -> 2 -> 3 -> 4 -> 5为一个联通子图，但是它还可以更大到1 -> 2 -> 3 -> 4 -> 5 -> 1，所以这才是一个强连通分量，因为这个子图的范围已经不能更大了。

那么怎么求一个有向图的强连通分量呢——现在还有一些知识点需要介绍。

2.时间戳（dfn[ ]）

在有向图的深度优先遍历中，记录每个点第一次被访问的时间的顺序，则这个顺序就是这个点的时间戳。在代码中我们用dfn[ ] 表示。 每个点的时间戳不一定，取决于从哪个点开始遍历。时间戳可以帮我们判断这个点是否已经遍历过，有vis的功能。

3.追溯值（low[ ]）

在有向图中，点x的追溯值为其子树满足一下条件的最小时间戳：

（1）该点已经访问过[ 有dfn值 ]

（2）存在一条从x出发的边以它为终点。

也就是说，从一开始我们初始化时，在找回到走过的点之前，我们的low值与dfn值相同。

我们来模拟一遍吧——设从点1 开始遍历：

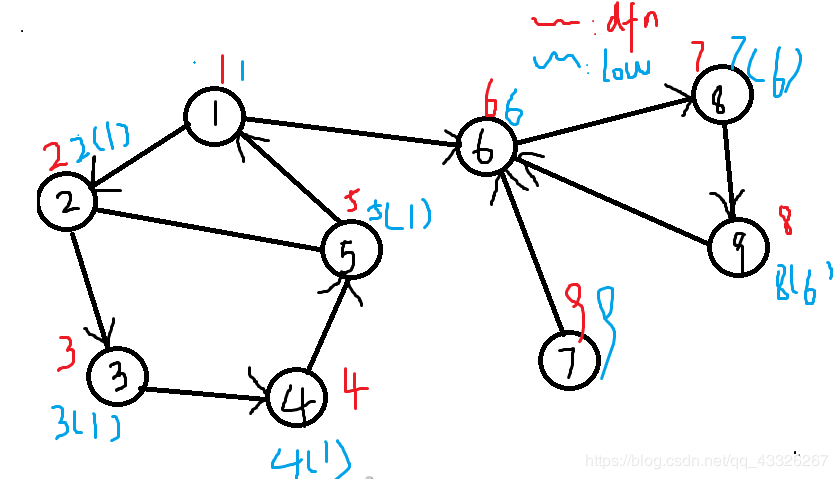
*解读：从1遍历到5时，如果选择先走5 -> 2，那么点2、3、4、5的low值都会追溯到2的时间戳，即2；但是紧接着我们点5继续遍历，会到点1并发现1也走过了并且dfn[ 1 ]的时间戳更早，所以点1、 2、 3、 4 、5 的追溯值都会更改为1的时间戳2。点6 、7 、8、9同理。最后这个图被分为了三个强连通分量。（左边的强连通分量中，点2~5的追溯值曾被更新为2，后更新为1，这一步省略）

由此我们也可以得出一个结论：一个有向图一定由k个有向图组成（k为任意非负整数），如图点7也单独算作一个强连通分量。

4.计算追溯值（寻找强连通分量的基本功）

1）初次访问点x，入栈（为了后期更新追溯值，需要存储路径），并初始化为low[ x ] = dfn [ x ] =++tot。栈可以用手写的，为stack[++tot] = x;

2）深度优先扫描点x连出去的边（x，y）；

3）开始判断：如果y点访问过了，则low [ x ] = min（low [ x ]，dfn[ y ]），y是目前可追溯到的最早结点。

如果y没有访问过，那么继续遍历点y，并设low [ x ] = low[ y ]以便在后来的操作中找到了更早的追溯值来更新点x的low。

4）特判·点x 回溯前，判断是否有low[ x ] == dfn[ x ]，有则说明点x为一个强联通分量的头结点，这时我们就从x的父节点开始弹出栈，直到x出栈，而弹出的点就组成一个强连通分量。

5.缩点

经过以上的探究，我们可以想到：既然这个图的强联通分量内，每个点都可以互相到达，那么是不是可以浓缩成一个点呢？答案当然是可以的~而且应用还比较广泛~即将一个由k个强连通分量组成的有向图缩成由k个点组成的有向图。如上文所示的图例可以缩成：

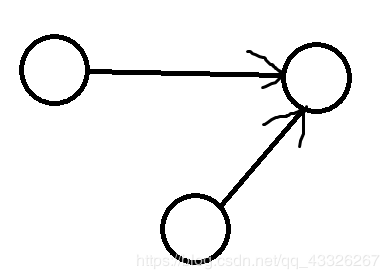
瞬间就简洁了很多有没有！（咳咳。）

那么我们如果要缩点该怎么操作呢——其实就是在上方求强连通分量的基础上加几个操作：在弹出路径的同时存下这个点的col[ ] ，即它所在的强联通分量的编号，这个我们用一个cnt来计数即可。至于涉及到后续操作，我们也可以考虑参考col的值再存一个缩点后的有向图。

结合目前为止的所有知识，我们可以敲一个模板题—— 缩点模板 。上面没看懂没关系，这里有详解：）

#include<bits/stdc++.h>
#define maxn 100000+5
using namespace std;
struct node
{
    int to,nxt;
    node(){}
    node(int tt,int nn)
    {
        to=tt;nxt=nn;
    }
}e[maxn],e_[maxn];

int head[maxn],k=0;
void add(int u,int v)
{
    e[k]=node(v,head[u]);
    head[u]=k++;
}

int dfn[maxn],low[maxn],col[maxn],stc[maxn],tot=0,top=0,cnt=0;
bool vis[maxn];
void tarjan(int x)
{
    vis[x]=1;
    dfn[x]=low[x]=++tot;
    stc[++top]=x;//初始化

    int y;
    for(int i=head[x];~i;i=e[i].nxt)
    {
        y=e[i].to;
        if(!dfn[y])//y没有访问过
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
        }

        else if(vis[y])//访问过并且在栈内（因为有可能访问过但是不在栈内，被弹出过了）
        {
            low[x]=min(low[x],dfn[y]);
        }
    }

    if(dfn[x]==low[x])//特判
    {
        cnt++;//强连通分量计数
        do{
            y=stc[top--];
            col[y]=cnt;//存
            vis[y]=0;//出栈后vis也自动更新，也就是说此处dfn不能完全代劳vis
        }while(x!=y);//只要还没有弹出到这个追溯点
    }
}

int head_[maxn],kk=0;
void add_(int u,int v)
{
    e_[kk]=node(v,head_[u]);
    head_[u]=kk++;
}

int w[maxn],n,m,a,b,du[maxn],dis[maxn],ans=0,w_[maxn];
int main()
{
    memset(head,-1,sizeof head);
    memset(head_,-1,sizeof head_);
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>w[i];

    for(int i=1;i<=m;i++)
    {
        cin>>a>>b;
        add(a,b);
    }

    for(int i=1;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i);//有可能图不连通，所以要循环判断。
    }

    int x,y;
    for(int i=1;i<=n;i++)
    {
        for(int j=head[i];~j;j=e[j].nxt)
        {
            y=e[j].to;
            if(col[i]!=col[y])//不在同一个强连通分量
            {
                add_(col[i],col[y]);
                du[col[y]]++;//存入度
            }
        }
        w_[col[i]]+=w[i];
    }

    queue<int> q;
    for(int i=1;i<=cnt;i++) if(!du[i])
    {
        q.push(i);//入度为0的点优先考虑开始
        dis[i]=w_[i];
    }   


    while(!q.empty())
    {
        x=q.front();
        q.pop();
        for(int i=head_[x];~i;i=e_[i].nxt)
        {
            y=e_[i].to;
            dis[y]=max(dis[y],dis[x]+w_[y]);//类似于dp
            du[y]--;
            if (du[y]==0) q.push(y);//拓扑排序，可以找到最长路线
        }
    }

    for(int i=1;i<=cnt;i++)
    {
        ans=max(ans,dis[i]);//取最优（我也不知道数据有没有负点权）
    }

    cout<<ans<<endl;
    return 0;
}

当然，这个模板的话无向图也是可以使用的。

还有一个例题： 间谍网络

二、割点与桥（for无向联通图）

其实有向图也可以由割点，但是和这里的算法不大一样，暂时不讲。

1、割点

若对于点x，删去后图G（V，E）被划分为两个及以上的子图，则称x为割点。

举个例子——还是之前那个图

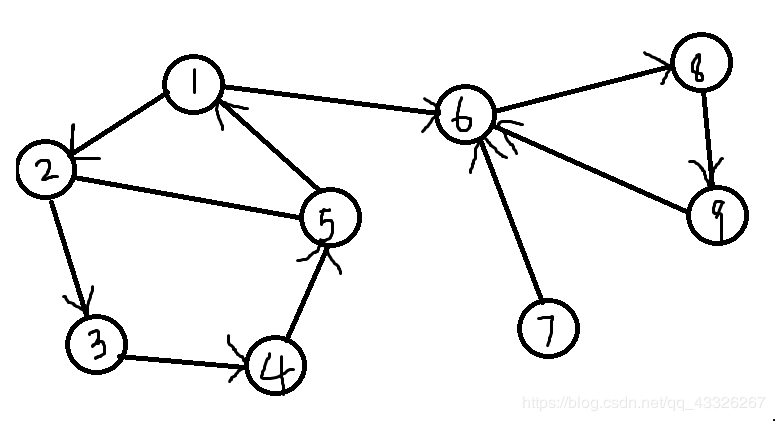
去掉点1后，图分为2 - 5 - 4 - 3 - 2和6 - 7 - 8+9两个子图；去掉点6后，图分为1 - 2 - 3 - 4 - 5、7 - 8和9三个子图。所以点1 、6为这个图的两个割点。

同样的，我们通过一个模板题来练习一下： 割点模板

#include<bits/stdc++.h>
#define maxn 20000+5
using namespace std;
struct edge
{
    int to,nxt;
    edge(){}
    edge(int tt,int nn)
    {
        to=tt;nxt=nn;
    }
}e[(maxn << 3) + (maxn << 1)];//其实就是10倍。

int k=0,head[maxn];
void add(int u,int v)
{
    e[k]=edge(v,head[u]);
    head[u]=k++;
}

int dfn[maxn],low[maxn],tot=0,cnt=0,root,cut[maxn];
void tarjan(int x)//割点模板
{
    dfn[x]=low[x]=++tot;
    int flag=0;
    for(register int i=head[x];~i;i=e[i].nxt)
    {
        int y=e[i].to;
        if(!dfn[y])
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if(dfn[x] <= low[y] && (x != root || ++flag > 1)) cut[x]=1;//flag自动计数
        }
        else low[x]=min(low[x],dfn[y]);
    }
}

int n,m,a,b;
int main()
{
    memset(head,-1,sizeof head);
    scanf("%d%d",&n,&m);
    for(register int i=1;i<=m;i++)
    {
        scanf("%d%d",&a,&b);
        add(a,b);
        add(b,a);
    }

    for(register int i=1;i<=n;i++)
    {
        if(!dfn[i]) root=i,tarjan(i);//需要判定是否为开始的结点。
    }

    for(register int i=1;i<=n;i++)
        if(cut[i]) cnt++;

    printf("%d\n",cnt);
    for(register int i=1;i<=n;i++)
    {
        if(cut[i]) printf("%d ",i);
    }
    return 0;
}

2、桥

对于一个无向图G（V，E），若边x删去后达到同删去割点后一样的效果，则称边x为桥（or 割边）。

如上图，边（1,6） 、（6,9）为两个桥。

应该还是挺好理解的。

3、判定桥

由桥的定义我们可以得出：若一条边（x，y）为桥，那么从x所在连通块到y所在连通块的路径有且仅有这一条路。所以我们可以利用这一点——如果无向边（x，y）为桥，则一定存在点x的子节点y满足 dfn[ x ] < low[ y ]，也就是说没有别的路可以再到达x，否则dfn[ x ]会被更新。这个如果不理解的话可以手动模拟一下理解，这里就不举例了：）

• 注：

1）图可能不连通，tarjan要用for循环筛没走过的点。（前文讲过了）

2）存无向图的时候涉及双向，所以从0开始存边会方便些，tarjan的末尾判断是否这条路是返回去的路。

核心代码如下：

void tarjan(int x, int in_edge)
{
    dfn[x] = low[x] = ++tot;
    for(int i = head[x]; ~i; i = e[i].next){
    int y = e[i].to;
    if(!dfn[y])
    {
        tarjan(y, i);
        low[x] = min(low[x], low[y]);
        if(dfn[x] < low[y]) bridge[i] = bridge[i ^ 1] = true;
        else if(i != (in_edge ^ 1)) low[x] = min(low[x], dfn[y]);
    }
}

存in_edge时就要注意到这条边的反向是否刚好为它的顺序与1。

三、双联通分量（for 无向图）

1.点双联通分量

若一张无向连通图不存在割点, 则称它为”点双连通图”.无向图的极大点双连通子图被称为”点双连通分量”, 简记为”v-DCC”。

一张无向连通图是”点双连通分量”, 当且仅当满足下列两个条件之一:

1) 图的顶点数不超过2。
2) 图中任意两点都同时包含在至少一个”简单环”指的是不自交的环,也就是我们通常画出的环。

这样就可以保证图不存在割点。具体证明方法这里就不解释了：）

若某个节点为孤立点，则它自己单独构成一个v-DCC. 除了孤立点以外，点双连通分量的大小至少为2，根据v-DCC定义中的”极大”性，虽然桥不属于任何eDCC，但是割点可能属于多个v-DCC。
为了求出”点双连通分量”，需要在Tarjan算法的过程中维护一个栈,。也就类似于我们前文所说的割点的求法。是不是和前文的缩点很类似呢！！！！！它们真的就长得挺像。但从某种程度上说，还是要复杂一些。

为了存从stack弹出来的结点构成的点双联通分量，我们还需要开一个vector< int >。

核心代码如下：

void tarjan(int x)
{
    dfn[x] = low[x] = ++tot;
    stc[++top] = x;
    if(x == root && head[x] = 1)
    {
        dcc[++cnt].push_back(x);
        return;
    }

    int flag=0;
    for(int i = head[x]; ~i; i = e[i].next)
    {
        int y = e[i].to;
        if(!dfn[y])
        {
            tarjan(y);
            low[x] = min(low[x], low[y]);

            if(dfn[x] <= low[y])//判定到了割点。
            {
                if(x != root || ++flag > 1) cut[x] = 1;
                cnt++;
                int z;
                do
                {
                    z = stc[top--];
                    dcc[cnt].push_back(z);
                }while(z != y);//依次出栈
                dcc[cnt].push_back(x);//特别要加上x
                //但是x不能弹出，因为它可能涉及到多个点双联通分量。

            }
        }else low[x] = min(low[x], dfn[y]);
    }
}

2.边双联通分量

如点双联通分量的定义：边双联通分量就是不存在桥的最大边双联通子图。这里就比点双联通分量要简单的多了——直接去掉所有的桥就行了。每一个连通块就是一个e-DCC。

我们在tarjan中标记所有的桥，再对无向图深优遍历一遍即可。

你看解释都简洁了好多

下面是核心代码：

void tarjan(int x, int in_edge)
{
    dfn[x] = low[x] = ++tot;
    for(int i = head[x]; ~i; i = e[i].next)
    {
        int y = e[i].to;
        if(!dfn[y])
        {
            tarjan(y, i);
            low[x] = min(low[x], low[y]);
            if(dfn[x] < low[y])
                bridge[i] = bridge[i ^ 1] = true;
        }
        else if(i != (in_edge ^ 1)) low[x] = min(low[x], dfn[y]);
    }
}

以上就是本次的全部内容啦！！！！！！！！！！

最后附上一个挺不错的题： 矿场搭建

迎评：）

——End——