线性代数

如果我们有两个 维数相同 的向量，他们的点积就是对应位置的数相乘，然后再相加：

看起来非常简单不是，但事实上，点积的真实含义将是目前学习中最大的难题。

从向量空间角度来说，就是

同时，值得说明的是，点积符合 对称性：

如果只是公式的话，我们可以用 交换律 证明。

同样，如果延伸到图形，我们可以构造 两个对称向量（即等腰三角形的腰），并由 近似三角形 性质推出证明。

以上证明较为容易，就不花时间再讲。

重点是，如何将 点积的公式 和 向量空间 联系起来。

当然，它们之间的联系是 对偶性的，只是在结果上共通，并不能用 抽象数学 的方式理解。

从上篇分享我们可以看到一个绝妙的结论，如果将二维矩阵压缩为一维，并计算 目标向量 的值，

则公式与 点积公式 完全一致（不过点积是向量与向量的关系，而这个公式是变量的线性变化）。

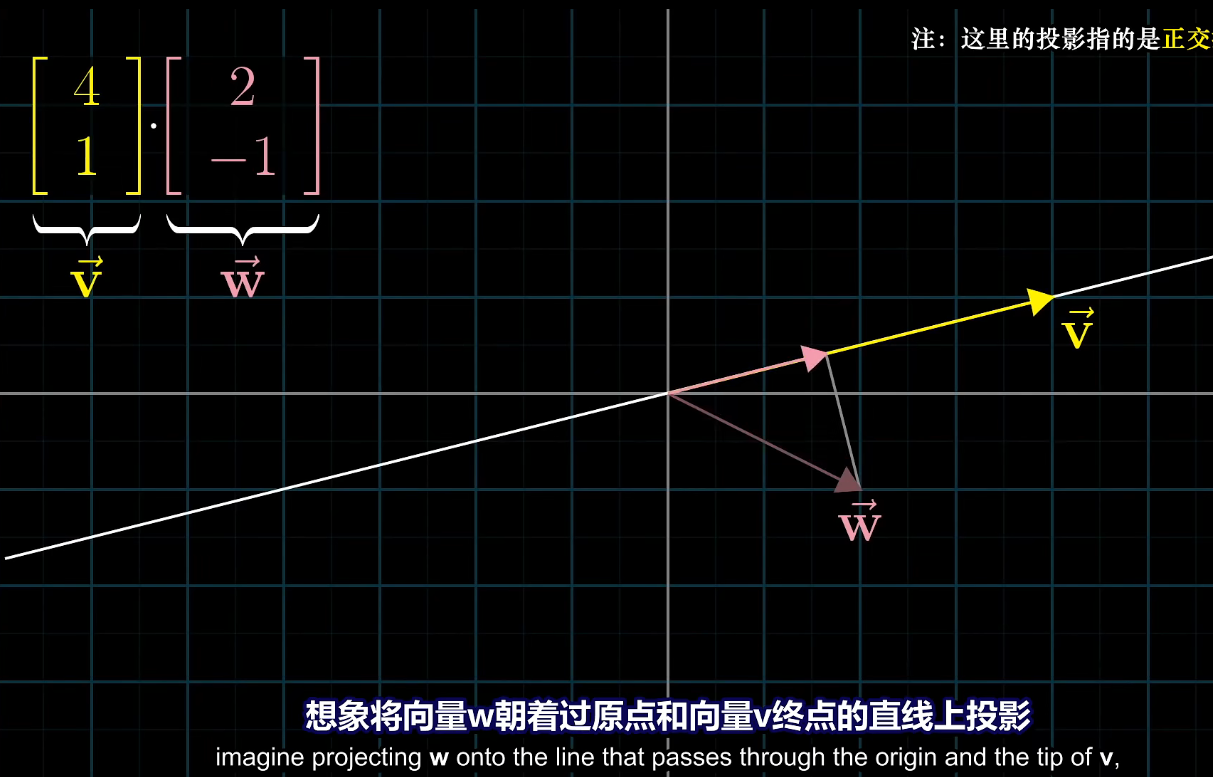
如果我们将这个数轴放到二维向量空间中（视作点积中的 一个向量 也可以）

则可以通过 对称性和近似性 求出它与基向量的 基准值，并由这个新的基准值计算 与另一个函数的点积 即可。

值得一说的是，若将数轴上的向量与基向量视为 对称 ，则可推出全等，

进而得到 基准值 就是此数轴上向量的 $x, y$ 坐标。

综上所述，点积一节证毕。