原题链接1

原题链接2

A. 求余 1

2021 % 20 = 1

B. 双阶乘 59375

public class Main {

    public static void main(String[] args) {

        int n = 2021, ans = 1;
        while(n > 0)  //for (int i = 1; i <= 2021; i += 2) 也行
        {
            ans = (ans * n) % 100000;
            n-=2;
        }
        System.out.println(ans);
    }

}

C. 格点 15698

public class Main {

    static long res;

    public static void main(String[] args) {

        for (int x = 1; x <=2021; x++)
            for (int y = 1; x * y <=2021; y++)
                res++;

        System.out.println(res);
    }
}

D. 整数分解 691677274345

我参考别人做的
一个数分解成五个正整数之和第四和第五个数只有remain - 1种情况 (用笔模拟一下就知道了)

public class Main {

    public static void main(String[] args) {

        int n = 2021;
        long res = 0;

        for(int i = 1;i <= n;i++)
            for(int j = 1;j <= n;j++)
                for(int k = 1;k <= n;k++)
                {
                    int remain = n - i - j - k;
                    if(remain <= 1) break;

                    res += (remain-1);
                }

        System.out.println(res);
    }
}

y总的隔板法 思路真不错
一个方程的解都可以转换为一个放隔板的方式。反过来也是一样。所以原方程正整数的解等于这样摆放隔板的方案数。
一共有2021-1=2020个空，要从中挑4个位置放隔板，所以是 组合数 C(2020, 4) = 2020*2019*2018*2017/(1*2*3*4)

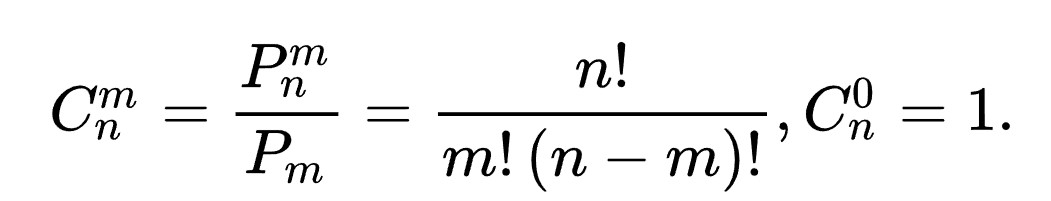
public class Main {

    public static void main(String[] args) {

        long res = 1;
        for (int i = 2020, j = 1; j <= 4; i --, j ++ )
            res = res * i / j;

        System.out.println(res);
    }
}

E. 城邦 4046

并查集+最小生成树 因为是填空题，所以可以用稍慢的Prim算法，用并查集实现。(当然Kruskal更好，但代码多)

import java.util.ArrayList;

class Edge
{
    int a,b,c;  //c是边权

    Edge(int a, int b, int c) {
        this.a = a;
        this.b = b;
        this.c = c;
    }

}

public class Main {

    static int N = 2030, M = N * N / 2;  //边数M = C(n, 2) ，这里没用上

    static int n = 2021, m;
    static int[] p = new int[N];  //并查集
    static ArrayList<Edge> e = new ArrayList<>();  //用数组的话就是e[M]

    static int find(int x)  // 并查集
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    static int get(int x, int y)  //算边权
    {
        int res = 0;
        while (x != 0 || y != 0)  //只要有一个不为0就循环，都为0才退出!
        {
            int a = x % 10, b = y % 10;
            if (a != b) res += a + b;
            x /= 10; y /= 10;
        }
        return res;
    }

    public static void main(String[] args) {

        for (int i = 1; i <= n; i ++ ) p[i] = i;  //初始化并查集

        for (int i = 1; i <= n; i ++ )
            for (int j = i + 1; j <= n; j ++ )
            {
                e.add(new Edge(i, j, get(i, j)));
                m++;  //任意两个城邦之间，都有一座桥直接连接。
            }

        e.sort((o1, o2)->{
            return o1.c - o2.c;  //按边权从小到大排序
        });

        int res = 0;
        for (int i = 0; i < m; i ++ )  //m其实就是e.size()，用后者更好
        {
            int a = e.get(i).a, b = e.get(i).b, c = e.get(i).c;
            if (find(a) != find(b))
            {
                res += c;
                p[find(a)] = find(b);  //加到一个集合
            }
        }

        System.out.println(res);

    }
}