A. Game

题意：
$n个只包含0和1的数组,你一开始在a[1]位置，求走到a[n]位置的最小代价$
$如果a[i]=a[i+1]=1,你可以从i走到i+1,代价为0$
$如果a[i]=a[j]=1[i<j]，你可以从i走到j,代价为j-i,只能走一次$
思路：
$因为第二种走法只能走一次$
$所以找到第一个连续的一的最后一个位置L$
$和最后一个连续的一的第一个位置R$
$答案即为R-L$
时间复杂度：$On$

int n ;
int a[N] ;

signed main()
{
    cf
    {
        cin >> n ;
        fer(i,1,n) sf(a[i]) ;

        int l = -1 , r = -1 ;
        fer(i,1,n)
        {
            if(!a[i]) 
            {
                l = i - 1 ;
                break ;
            }
        }
        der(i,n,1)
        {
            if(!a[i])
            {
                r = i + 1 ;
                break ;
            }
        }

        de(r - l) ;
    }
    return 0 ;
}

B. Game of Ball Passing

题意：
$给你一个n个数的数组,a[i]表示i这个人传了a[i]次球$
$现在问你进行了最少多少次传球使得所有人都可以传完$
$每次传球从任意一个人开始,只要传给除他之外的人即可$
思路：
$把每次传球转化一下$
$等价于首先选一个i，使a[i]-1$
$然后在任意选2个不同的下标i,j,使a[i]-1,a[j]-1,可以进行无数次$

$不考虑首先选一个i，使a[i]-1的情况下$
$记录一下数组总和sum和数组最大值maxv$
$如果sum-maxv>=maxv$
$说明一次传球即可$

$考虑首先选一个i，使a[i]-1的情况下$
$那我们二分进行了多少次传球mid$
$如果mid次可以传球成功,说明mid可以变小$
$否则mid变大$

$mid次传球,等价于你可以先进行mid次选一个i，使a[i]-1$
$然后在任意选2个不同的下标i,j,使a[i]-1,a[j]-1,可以进行无数次$

$即sum-maxv>=maxv-mid即可$

时间复杂度：$On$

int n ;
int a[N] ;
int s , v ;

int get(int mid)
{
    if(s - v >= v - mid) return 1 ;

    return 0 ;
}

signed main()
{
    cf
    {
        cin >> n ;
        fer(i,1,n) sf(a[i]) ;

        s = 0 , v = 0 ;
        fer(i,1,n) s += a[i] , v = max(v , a[i]) ;

        if(!v)
        {
            puts("0") ;
            continue ;
        }

        int l = 1 , r = 1e10 ;
        while(l < r)
        {
            int mid = l + r >> 1 ;
            if(get(mid)) r = mid ;
            else l = mid + 1 ;
        }

        de(l) ;
    }
    return 0 ;
}

C. Weird Sum

题意：
$给你一个n*m的方格,每个方格c[i][j]都有一个颜色k,求$

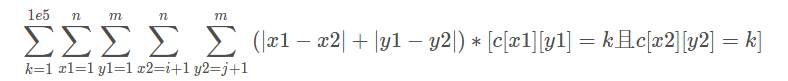
思路：
$首先|x1-x2|+|y1-y2|可以分开算$
$所以我们可以预处理所有颜色的不同的横坐标和纵坐标$

$现在问题等价于对于任意一个序列$
$a_1$ $a_2$ .......$a_n$
$求所有不同颜色的\sum_{i=1}^{n}{\sum_{j=i+1}^{n}|a[i]-a[j]|}$

$首先将数组排序之后$
$因为\sum_{i=1}^{n}{\sum_{j=i+1}^{n}|a[i]-a[j]|}=\sum_{i=1}^{n}{\sum_{j=1}^{i-1}|a[i]-a[j]|}$
$所以记录前缀和直接加即可$

时间复杂度：$Onmlognm$

int n , m ;
vector<int> g[N] ;
int res ;

void solve(vector<int> &v)
{
    sort(all(v)) ;
    int s = 0 ;
    for(int i = 0 ; i < sz(v) ; i ++)
    {
        res += v[i] * i - s ;
        s += v[i] ;
    }
}

signed main()
{
    cin >> n >> m ;

    vector<vector<int>> a(n + 1 , vector<int>(m + 1 , 0)) ;

    fer(i,1,n)
        fer(j,1,m)
        {
            sf(a[i][j]) ;
            g[a[i][j] * 2].pb(i) ;
            g[a[i][j] * 2 + 1].pb(j) ;
        }

    fer(i,1,2e5 + 10)
    {
        if(g[i].size())
            solve(g[i]) ;
    }

    de(res) ;
    return 0 ;
}

D. Integral Array

题意：
$给你一个n个数的数组,如果数组中没有出现a[j]/a[i],[a[j]>=a[i],1<=i,j<=n]$
$输出No$
$否则输出Yes$
思路：
$对于数组中的每个数,我们可以枚举它的倍数$
$假设对于i这个数,它的倍数为j$
$那么区间[ij,ij+i-1]中的任何一个数x/i=j$
$所以如果i这个数和x这个数都同时出现过的话$
$那么j也必须出现$
$如果j没有出现过的话,直接输出No即可$

时间复杂度：$时间复杂度:n/1+n/2+.....+n/n \approx nlogn$

int n , m ;
int a[N] ;
int cnt[N] ;
int tt[N] ;
int cc[N] ;

signed main()
{
    cf
    {
        cin >> n >> m ;
        fer(i,0,m * 2 + 10) cnt[i] = 0 , cc[i] = 0  ;
        fer(i,1,n) scanf("%d",&a[i]) , cnt[a[i]] = 1 , cc[a[i]] = 1;
        fer(i,1,m * 2 + 10) cnt[i] += cnt[i - 1] ;

        int f1 = 0 ;
        for(int i = 1 ; i <= m ; i ++)
        {   if(cc[i])
            for(int j = 1 ; j * i <= m ; j ++)
            {
                int l = j * i , r = j * i + i - 1 ;
                if(cnt[r] - cnt[l - 1])
                {
                    if(!cc[j]) f1 = 1 ;
                }
            }
        }

        if(f1) puts("No") ;
        else puts("Yes") ;
    }
    return 0 ;
}