快速排序的名字起的是简单粗暴，因为一听到这个名字你就知道它存在的意义，就是快，而且效率高！它是处理大数据最快的排序算法之一了。虽然 Worst Case 的时间复杂度达到了 O(n²)，但是人家就是优秀，在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好
快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。
基于“交换”的排序：根据序列中两个元素关键字的⽐较结果来对换这两个记录在序列中的位置

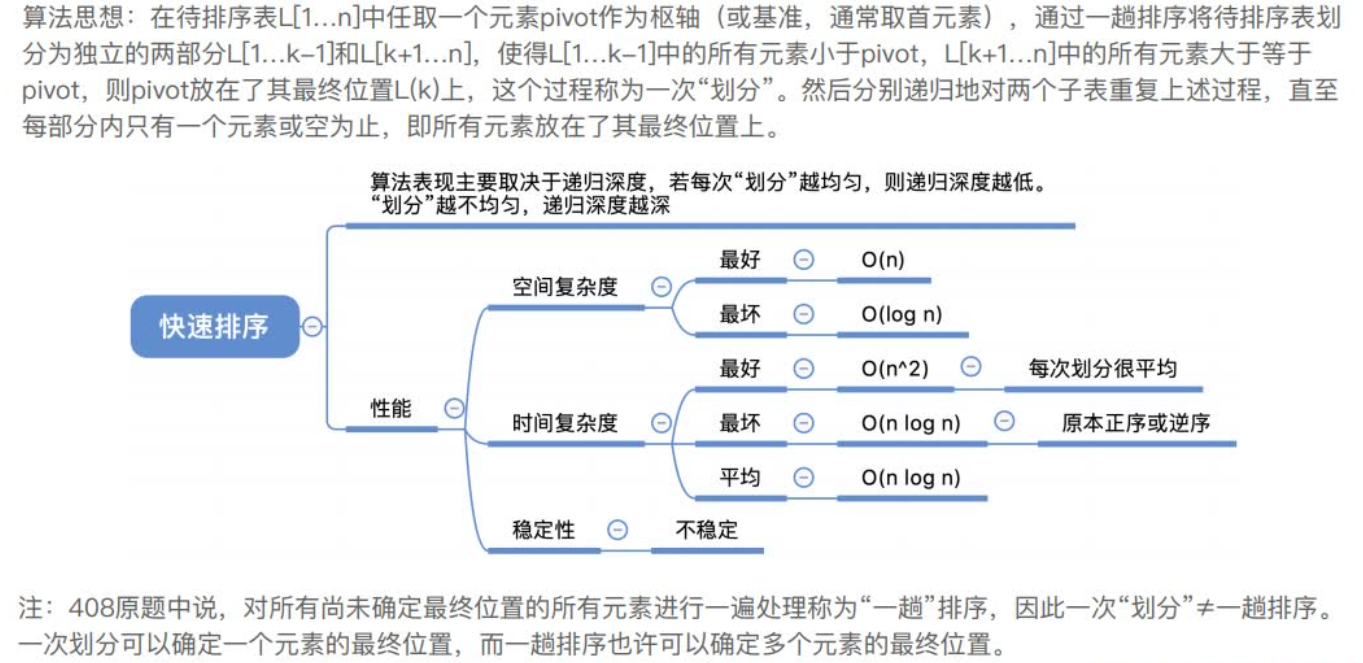
算法思想：在待排序表L[1…n]中任取⼀个元素pivot作为枢轴（或基准，通常取⾸元素），通过⼀趟排序将待排序表划分为独⽴的两部分L[1…k-1]和L[k+1…n]，使得L[1…k-1]中的所有元素⼩于pivot，L[k+1…n]中的所有元素⼤于等于pivot，则pivot放在了其最终位置L(k)上，这个过程称为⼀次“划分”。然后分别递归地对两个⼦表重复上述过程，直⾄每部分内只有⼀个元素或空为⽌，即所有元素放在了其最终位置上。

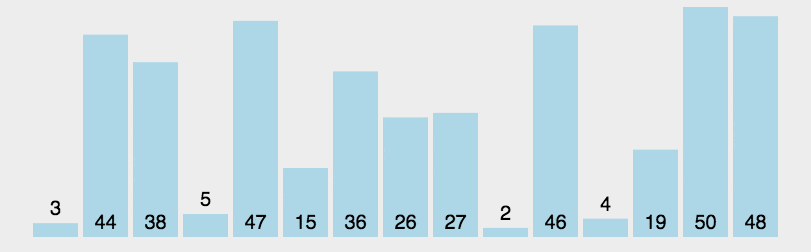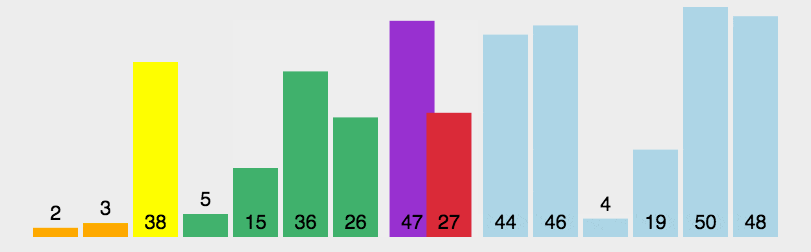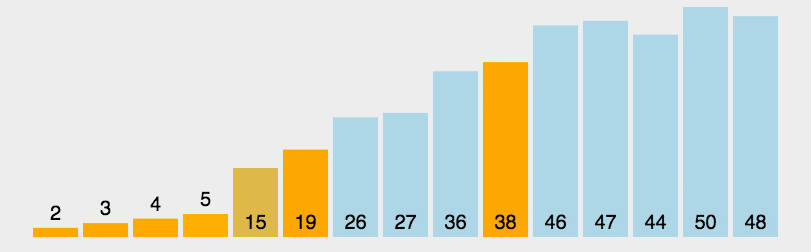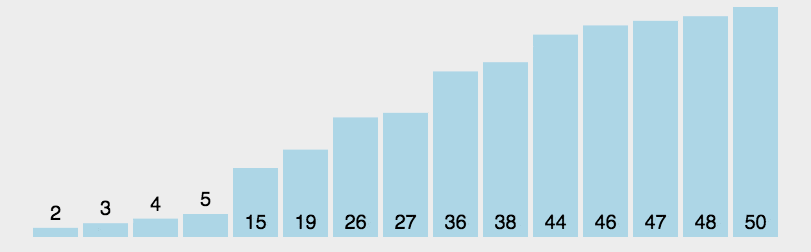
更⼩的元素都交换到左边，更⼤的元素都交换到右边

代码实现

C实例
typedef struct _Range {
int start, end;
} Range;

Range new_Range(int s, int e) {
Range r;
r.start = s;
r.end = e;
return r;
}

void swap(int x, int y) {
int t = x;
x = y;
y = t;
}

void quick_sort(int arr[], const int len) {
if (len <= 0)
return; // 避免len等於負值時引發段錯誤（Segment Fault）
// r[]模擬列表,p為數量,r[p]為push,r[–p]為pop且取得元素
Range r[len];
int p = 0;
r[p] = new_Range(0, len - 1);
while (p) {
Range range = r[–p];
if (range.start >= range.end)
continue;
int mid = arr[(range.start + range.end) / 2]; // 選取中間點為基準點
int left = range.start, right = range.end;
do {
while (arr[left] < mid) left; // 檢測基準點左側是否符合要求
while (arr[right] > mid) –right; //檢測基準點右側是否符合要求
if (left <= right) {
swap(&arr[left], &arr[right]);
left;
right–; // 移動指針以繼續
}
} while (left <= right);
if (range.start < right) r[p] = new_Range(range.start, right);
if (range.end > left) r[p] = new_Range(left, range.end);
}
}

算法效率分析

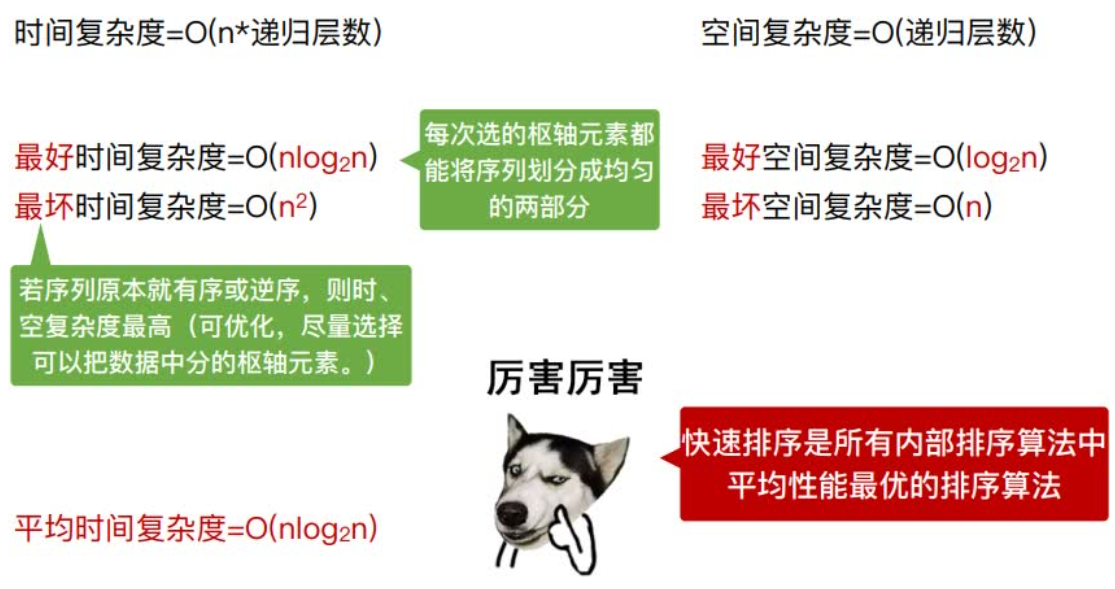
总结