直线绘制：Bresenham算法

直线在计算机上是以像素点的连接所形成的，这里我用模拟二维数组模拟像素点，每一个二维坐标为一个像素点，学习并实现Bresenham算法。

因为直线肯定不会全部穿过像素点，所以传统计算会产生浮点运算，而Bresenham算法的优点就是消除浮点运算，只用加减，提高效率。

基本思想

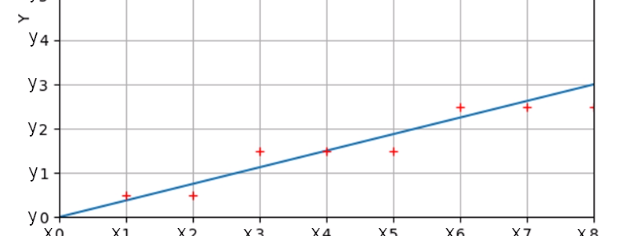
我用二维坐标系模拟一个像素网格，每一个网格交点为一个像素点。我们取像素点 （0，0）和 （8，3）连接起来如图，红色十字为直线与纵轴的交点所在网格的中点，因为交点只可以是整数，所以实际上我们只可以画在网格的交点上。

基本思想，当直线与网格交点的纵坐标小于当前网格中点的纵坐标时，我们把像素点画在中点下面的坐标上，当直线与网格交点的纵坐标大于或者等于当前网格中点的纵坐标时，我们把像素点画在中点上面的坐标上。

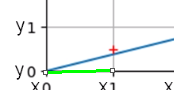
以第一个点为例，我们可以看到蓝色的线与 x = 1 直线的交点比当前网格红色中点小，所以我们画在下面的坐标点（1，0）上，并连接上一个像素点（0，0）；

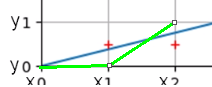
看第二个点，蓝色直线与 x = 2 这条直线的交点比当前网格中点红色标记大，所以我们画在上面坐标点（2，1）上，并连接上一个像素点（1，0）；

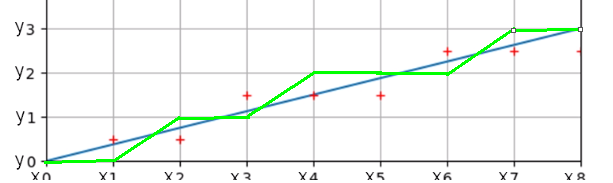
以此类推，我们把剩下的都画出来，可以看到实际的 ” 直线 “ 是绿色的线组成的，只不过像素非常非常小，组合起来之后，我们肉眼看到的就是一条直线了，这就是基本思想了，我分三步写一下代码：

原始代码

上面的思想有一个局限性，只有在第一象限内且直线斜率小于1的情况下才可以成立，也就是只满足在八分之一圆内画直线。

我先写局部算法，等会在扩展到整个圆。

定义数组 g 初始化都为 0 ，表示没有被标记。

首先我们要从起点开始，初始化数据：

x = begin.x //当前点的x坐标
y = begin.y //绿色的线的y坐标
k = (end.y - begin.y) / (double)(end.x - begin.x) //直线的斜率
dy = begin.y + k; //蓝色直线与x = ？的纵坐标 也就是我们用dy表示当前的截距 下面会讲为啥初始化这样
middle = begin.y + 0.5; //每个格子的中点纵坐标也是截距

我们从起点遍历一下，x的坐标每次 +1，然后判断此时蓝色的线与x的直线的交点的纵坐标dy与此时中点，如果中点大，则数组 g[ x，dy下取整]标记为 1 ，否则，

g[ x, dy上取整]标记为 1，接着x++ 进入下一个格子，此时middle中点坐标和y要变化：

为了确定 middle和 dy的变化，我们要明白斜率的几何意义是什么？

斜率的几何意义是 x坐标每次+1，y所增长的长度。所以上图中（0，0）为起点时，x为1时，dy的纵坐标就是k，x为2时，dy的大小就是2k；

因为我们的起点不一定为（0，0），所以我们的第一个dy是起点的纵坐标+斜率k，x每次+1，我们的dy也要+1；

而middle变化，我们发现midlle是上一个蓝绿色点的y值+1，所以当判别式成立时，middle+1；

（ 其实上述middle是有误差的，当middle==dy时，我们规定判别式也成立，此时y+1，但是middle并没有+1，这是因为当二者相等时，像素点判定在上面还是下面都是可以的，我们认为规定在上面，所以产生了误差，不过最后结果是不会产生影响的 ）

#include <iostream>
using namespace std;

const int N = 50;
int g[N][N];    //定义50*50的二维像素数组

struct Point
{
    int x, y;
}point;          //起点和终点坐标我用结构体表示

void Bresenham1(Point begin, Point end)      //单一方向且有浮点数的第一版本
{
    double k = (end.y - begin.y) / (double)(end.x - begin.x);  // 斜率
    double middle = begin.y + 0.5;  //中点
    double dy = begin.y + k;        //截距
    int x = begin.x;                //此时真正像素点的x轴坐标
    int y = begin.y;                //此时的真正像素点y的坐标
    while (x <= end.x)              //遍历，一直到终点
    {
        if (dy >= middle)           //如果交点大于中点
        {
            y += 1;                 //取上面的点
            middle += 1;            //下一个middle要+1
        }
        g[x][y] = 1;                //标记数组
        x++;                        //遍历下一个点
        dy += k;                    //根据几何意义，截距+k
    }
}

int main()
{
    Point begin, end;                   //  起点和终点
    int x1, x2, y1, y2;
    cin >> x1 >> y1 >> x2 >> y2;        //输入起点和终点坐标
    begin = { x1,y1 };
    end = { x2,y2 };

    Bresenham1(begin, end);             

    for (int i = 0; i < N; i++)         // 打印数组 
    {
        for (int j = 0; j < N; j++)
        {
            cout << g[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

正常的二维坐标系是右为 x轴正方向，上为 y轴正方向，但是我在二维数组中模拟，c++数组中右边为 y的正方向，下为x轴正方向，所以测试视图方向是向右下的。

我们输入（0，0）和（8，3）效果如图：

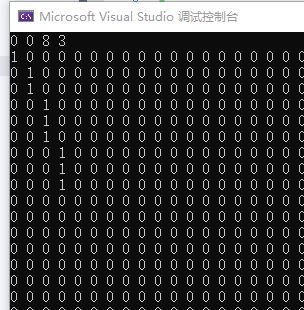
可以看到 1 所连成的像素点是正确的。

但是上述代码我们用到了浮点数，那么怎末去掉浮点数呢？

去点浮点数运算的代码

我们的目的是画直线，也就是判断middle和dy的关系，所以middle和dy的具体数值没有影响，只是他们的大小比较影响，都减去一个相同的数是不变的，我们发现，midlle和dy都有一个相同的begin.y,所以可以都减去begin.y，意义不变，方便下面运算。

 middle =  0.5;  //中点
 dy =  k = (end.y - begin.y) / (double)(end.x - begin.x);        //截距

所以我们middle和dy都乘以一个数最后的大小比较结果也是不会变的，所以去除浮点数一个很重要的知识点是乘以一个很大的数，让他变成整数，最简单的就是乘以他们的公倍数，举个例子：

我们的 dy等于斜率 k，而k 是y除以x得到的，x是整数，y也是整数，但是除出来就是小数了，怎末办？我们乘以一个(end.x - begin.x)就可以了，dy乘以了(end.x - begin.x)那么middle也要乘以(end.x - begin.x)，但是middle乘以了(end.x - begin.x)它有0.5，还是小数，所以要乘以2倍的(end.x - begin.x)就都可以消除小数了。所以最后是：

middle =  (end.x - begin.x);        //中点
dy = k * 2 * (end.x - begin.x) = 2 * (end.y - begin.y);        //截距

middle和dy都变了，更新他们时也要变化，

dy += 2 * (end.y - begin.y)； //以前根据意义时+k，现在变了，要乘以 2 * (end.x - begin.x)，化简一下。
middle +=  2 * (end.x - begin.x);  //以前时+1，现在是要乘以 2 * (end.x - begin.x)，

所以去除浮点数的代码是：

#include <iostream>
using namespace std;

const int N = 50;
int g[N][N];    //定义50*50的二维像素数组

struct Point
{
    int x, y;
}point;          //起点和终点坐标我用结构体表示

void Bresenham1(Point begin, Point end)      //单一方向且没有浮点数的第二版本
{
    int middle = (end.x - begin.x);       //中点  具体数值没有意义，只是用来比较 上面有作解释
    int dy = 2 * (end.y - begin.y);        //截距  具体数值没有意义，只是用来比较 上面有作解释
    int x = begin.x;                //此时真正像素点的x轴坐标
    int y = begin.y;                //此时的真正像素点y的坐标
    while (x <= end.x)              //遍历，一直到终点
    {
        if (dy >= middle)           //如果交点大于中点
        {
            y += 1;                 //取上面的点
            middle += 2 * (end.x - begin.x);//
        }
        g[x][y] = 1;                //标记数组
        x++;                        //遍历下一个点
        dy += 2 * (end.y - begin.y);//
    }
}

int main()
{
    Point begin, end;                   //  起点和终点
    int x1, x2, y1, y2;
    cin >> x1 >> y1 >> x2 >> y2;        //输入起点和终点坐标
    begin = { x1,y1 };
    end = { x2,y2 };

    Bresenham1(begin, end);             //调用函数

    for (int i = 0; i < N; i++)         // 打印数组 
    {
        for (int j = 0; j < N; j++)
        {
            cout << g[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

起点（2，1），终点（12，3）的效果图：

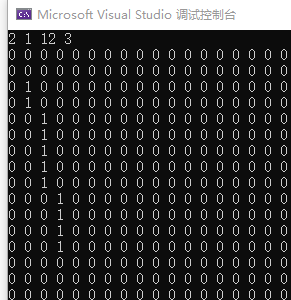
完整的Bresenham算法

待更新。。