Trie是什么 ?
字典树 : 见名知意(在树上进行查询)。
跟字典相关的必定与查询有密切的关系,
查询就需要一定的媒介作为支撑,树就为这种查询提供支撑。
Trie做什么 ?
实现字符串快速检索的多叉树结构。
常见的字符串转化:小写字母或者大写字母组成的字符串,数字组成的字符串,01编码组成的字符串。
Trie有什么 ?
Trie 的每个节点都拥有若干个字符指针,就是说每个节点有多个子节点,通俗一点就是相当于古代
的大少爷可以有多个妻子。
Trie干什么 ?
1、插入(将一个字符串插入到字典树上)
2、检索(检索一个字符串 S 在Trie 上是否存在)
侃了这么多,看看这货到底是个啥 ?
假设有单词 : cab , cef , da 这样三个单词,那么这样三个单词组成的图是什么样的呢 ?
看下图 : (通常还要在末尾进行标记一下,表示到字符串的末尾)
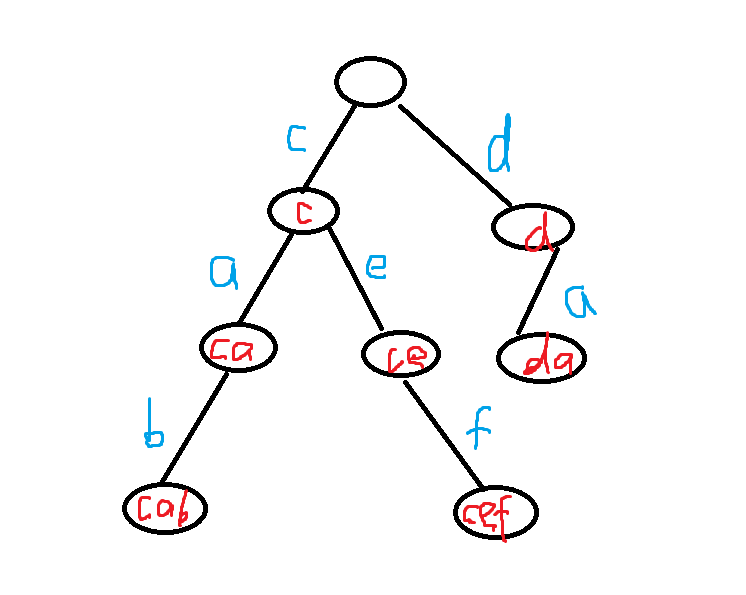
怎么实现这个玩意呢 ?
插入 :
像每个单词拼写一样,单词的开头就相当于是我们的根,从根节点出发,向儿子节点前进。
在向下走的过程中,看有没有当前这个字符的节点,如果有这个节点,就顺着这个节点继续
往下走,如果没有这个节点,就在这个节点之下再创建一个节点。
拿一个例子来说:
比如上图的 cab 和 cef, 先插入第一个字符串,从根节点出发,第一个字符是 c,我们发
现没有这个字符的节点,所以创建一个节点,将指针节点进行指向,然后一直向下移动,知道
字符串结尾。再插入第二个字符串,先检测第一个字符是否存在,我们发现存在,所以不用
创建,直接向下移动指针节点即可。
可以发现:
一个节点最多可以有26个孩子。
检索:
只需要将字符串遍历一遍,顺着根节点下来看这条路径上是否有不存在的值,即 0,如果
没有到末尾就发现有 0 ,说明这个字符串不存在,反之即存在。
Code :
插入:
void insert(char str[]) {
int len = strlen(str),p = 0; // p 作为根节点从 0 开始
for(int i = 0; i < len; i ++) {
int ch = str[i] - 'a';
if(trie[p][ch] == 0) trie[p][ch] = ++ idx; // 创建新的节点
p = trie[p][ch]; // 指针移动
}
End[p] = true; // 在末尾进行标记
return ;
}
检索:
bool query(char str[]) {
int len = strlen(str),p = 0;
for(int i = 0; i < len; i ++ ){
int ch = str[i] - '0';
if(trie[p][ch] != 0) {
p = trie[p][ch];
} else {
break; // 及时跳出
}
}
return true;
}
Example: 前缀统计
题目链接: https://www.acwing.com/problem/content/144/
题目描述:给定N个字符串S1,S2…SN,接下来进行M次询问,每次询问给定一个字符串T,求S1~SN中有多少个字符串是T的前缀。
输入字符串的总长度不超过106,仅包含小写字母。
输入格式
第一行输入两个整数N,M。
接下来N行每行输入一个字符串Si。
接下来M行每行一个字符串T用以询问。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
输入样例:
3 2
ab
bc
abc
abc
efg
输出样例:
2
0
析题得说: 统计每个字符串出现的个数即可,用一个cnt[]数组记录每个字符串出现的个数,然后进行检索要处理的字符串,累加结果(模板题)
AC代码:
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int SIZE = 1e6 + 10;
int trie[SIZE][26],cnt[SIZE];
char str[SIZE];
int n,m,idx = 0;
int main(void) {
void insert();
int query();
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i ++) {
scanf("%s",str);
insert();
}
while(m --) {
scanf("%s",str);
printf("%d\n",query());
}
return 0;
}
void insert() {
int p = 0;
for(int i = 0; i < strlen(str); i ++) {
int ch = str[i] - 'a';
if(trie[p][ch] == 0) trie[p][ch] = ++ idx;
p = trie[p][ch];
}
cnt[p] ++; // 统计该字符串的个数
return ;
}
int query() {
int p = 0,res = 0;
for(int i = 0 ; i < strlen(str); i ++) {
int ch = str[i] - 'a';
if(trie[p][ch] != 0) {
p = trie[p][ch];
res += cnt[p]; // 将以该字符结尾的数量累加,最后结果就是前缀字符串的数量
} else {
break;
}
}
return res;
}


good