原文链接

堆的定义

• 堆：完全二叉树 + 满足某种条件（父亲结点比左右儿子小 或 父亲结点比左右儿子大）

• 堆（heap）有时被称为优先队列（priority queue）。堆和队列有相似地方，在堆底插入元素，在堆顶取出元素，但是堆中元素的排列不是按照到来的先后顺序，而是按照一定的优先顺序排列的

算法分析

以小根堆为例
小根堆：父亲结点比左右儿子小

堆最好能满足一下五个功能
1. 插入一个数
2. 求集合中的最小值
3. 删除最小值
4. 删除集合中任意一个数
5. 修改集合中任意一个数

STL中的priority_queue可以实现功能1,2,3
而我们如何自己手写一个堆可以实现功能1,2,3,4,5

如何存储堆？
- 使用一维数组，下标存1到n
根结点下标为1 （不建议从0开始）
x的左儿子下标为2x
x的右儿子下标为2x+1

每个功能对应代码
1. 插入一个数：heap[++size_] = x; up(size_);
2. 求集合中的最小值 : heap[1];
3. 删除最小值: heap[1] = heap[size_]; size_ --; down(1);
4. 删除集合中任意一个数 heap[k] = heap[size_]; size_ --; down(k); up(k);
5. 修改集合中任意一个数 heap[k] = x; down(k); up(k);

解释一下代码：heap[k] = heap[size_]; size_ --; down(k); up(k);
- 在删除数组中一个数时，因为我们删除末尾元素是很方便的，但删除中间的不是很方便，所以我们先把末尾元素赋值给当前要删的位置，然后总长度减一，最后再down(k)一下，up(k)一下，这两个函数实际上只会执行一个，都写上可以省去分类讨论

down(k)操作是往下维护这个堆
down(k)操作：将当前点k跟它的儿子们相比，把最小的作为新的父结点，也就是继续一次交换，然后递归下去，知道不需要进行交换，就能保持小根堆为止

up(k)操作是往上维护这个堆
up(k)只需要把k和它的父结点k / 2进行比较就行，如果父结点较大，那就交换他们俩，然后递归下去，直到不需要交换为止

down()和up()操作的时间复杂度都与是树的高度直接相关的，所以是$log(n)$的

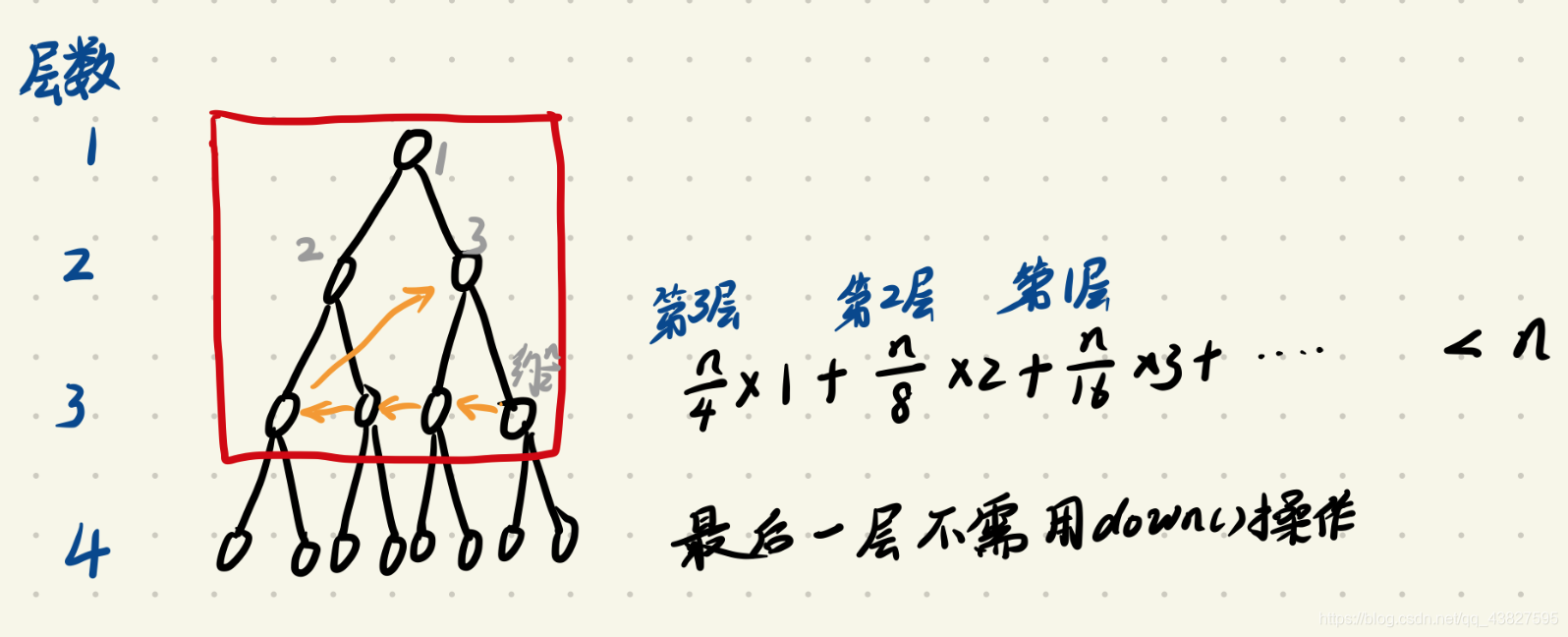
如何初始化堆？
for (int i = n / 2; i > 0; i --) down(i);
该操作时间复杂度为O(n)

理由如图所示：

down()和up()函数代码模版

// 值变化，往下维护
void down(int u) {
    int t = u; // t记录最小值
    if (2 * u <= size_ && h[2 * u] < h[t]) t = 2 * u; // 左儿子存在，且值比父亲小
    if (2 * u + 1 <= size_ && h[2 * u + 1] < h[t]) t = 2 * u + 1; // // 右儿子存在，且值比父亲小
    if (t != u) {
        swap(h[t], h[u]);
        down(t);
    }
    return;
}

// 值变化，往上维护
void up(int u) {
    if (u / 2 > 0 && h[u / 2] > h[u]) {
        swap(h[u / 2], h[u]);
        up(u / 2);
    }
    return;
}

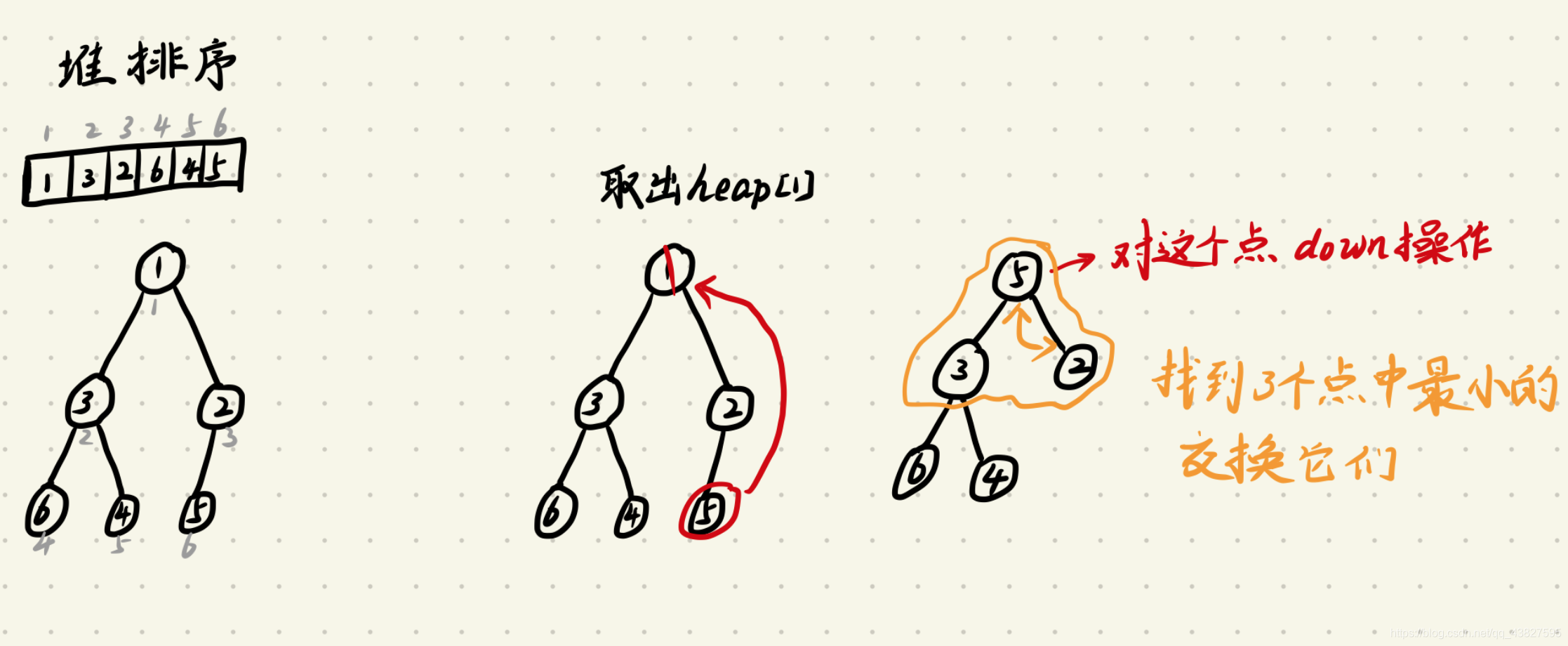
堆排序代码模版

题目描述：
对一个数组从小到大排序

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

C++代码模版

#include <iostream>
#include <algorithm>
using namespace std;

int n;
const int N = 100010;
int h[N], size_;

void down(int u) {
    int t = u;  // t记录最小值
    if (2 * u <= size_ && h[2 * u] < h[t]) t = 2 * u; // 左儿子存在，且值比父亲小
    if (2 * u + 1 <= size_ && h[2 * u + 1] < h[t]) t = 2 * u + 1; // // 右儿子存在，且值比父亲小
    if (t != u) {
        swap(h[t], h[u]);
        down(t);
    }
    return;
}

void up(int u) {
    if (u / 2 > 0 && h[u / 2] > h[u]) {
        swap(h[u / 2], h[u]);
        up(u / 2);
    }
    return;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> h[i]; 
    size_ = n;

    // 初始化堆
    for (int i = n / 2; i > 0; i --) down(i); 

    while(n --) {
        cout << h[1] << " ";
        h[1] = h[size_];
        size_ --;
        down(1); 
    }

    return 0;
}